1.3. Связь напряженности электрического поля и потенциала

Предположим, что нам известен потенциал  электрического поля во всех точках пространства. Как найти напряженность поля в некоторой точке?

Выберем в пространстве, где существует электрическое поле, декартову прямоугольную систему координат. Перенесем некоторый пробный заряд q вдоль оси x на малое расстояние . Тогда работа электрического поля по перемещению зарядаq из одной точки в другую

,

где и () – начальная и конечная координаты заряда, а– изменение потенциала заряда.

С другой стороны по определению элементарная работа силы (на небольшом участке траектории) есть скалярное произведение векторов и приращения радиус-вектора :

,

где  проекции вектора силы на соответствующие оси прямоугольной системы координат.

Так как заряд перемещается вдоль оси , то его координатыине меняются:. Следовательно, получаем:

.

Приравнивая правые части полученных для величины выражений:, для проекции вектора напряженности на осьx получим:

, (1.9)

т.е. проекция вектора напряженности электрического поля на ось x равна производной потенциала по направлению оси x, или, другими словами, равна градиенту потенциала в этом направлении.

Аналогично, смещая заряд вдоль оси или вдоль оси, можно найти величины проекцийи:

, (1.9,а)

. (1.9,б)

Итак, все три компоненты вектора напряженности электрического поля известны:

. (1.9,в)

Вектор, стоящий справа в последнем уравнении, называется градиентом скалярной функции и обозначается. Таким образом

, (1.10)

т.е. две характеристики электрического поля – напряженность и потенциал связаны друг с другом. Зная потенциал в каждой точке пространства, где существует электрическое поле, можно определить вектор напряженностив каждой точке этого пространства, и наоборот.

В курсе математического анализа показывается, что , где вектор нормали к поверхности . Функциявозрастает наиболее быстро в направлении. Поскольку, вектортакже перпендикулярен поверхностии направлен в сторону, противоположную нормали, т.е. в сторону убывания потенциала.

1.4. Электрическое поле точечного заряда. Принцип суперпозиции

Определим напряженность и потенциал электрического поля точечного заряда q на расстоянии r от него. Поместим некоторый «пробный» положительный заряд на расстоянииr от заряда . Тогда на заряд действует сила, модуль которой определяется выражением (1.1)

.

По определению напряженности поля (1.3) находим

. (1.11)

Таким образом, величина напряженности электрического поля точечного заряда обратно пропорциональна квадрату расстояния от заряда до точки наблюдения. Согласно (1.3) вектор направлен так же, как и сила, действующая на «пробный» положительный заряд. Если зарядположительный, то векторнаправлен вдоль радиус-вектора(рис.1.3, а), проведенного от точечного заряда в точку наблюдения. Если заряд отрицательный, то векторнаправлен против вектора(рис. 1.3, б). Таким образом, для проекции векторана направление радиус-вектора, проведенного от точечного заряда в точку наблюдения, получится формула

, (1.11,а)

, если , и, если. Напряженность можно записать в векторном виде

. (1.11,б)

Теперь определим потенциал поля точечного заряда, для которого формула (1.10) имеет следующий вид

,

где  проекция вектора напряженности электрического поля на направление радиус вектора, проведенного от точечного заряда в точку, где определяются характеристики поля. Подставляя в нее значение из (1.11,а), получим дифференциальное уравнение с разделяющимися переменными:

,

далее интегрируем:

,

где С – константа интегрирования. На бесконечно большом расстоянии () получим. Имея ввиду нулевое значение потенциала бесконечно удаленных точек, получаем. Таким образом, потенциал поля точечного заряда

. (1.12)

Как потенциал, так и напряженность электростатического поля, подчиняются принципу суперпозиции, который является важнейшим свойством электрического поля. Согласно этому принципу, напряженность поля (потенциал), создаваемая в какой-либо точке пространства системой зарядов, равна векторной (скалярной) сумме напряженностей (потенциалов), создаваемых в этой точке каждым из зарядов

, (1.13)

. (1.14)

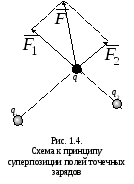
Принцип суперпозиции для напряженностей полей точечных зарядов следует из того опытного факта, что сила электрического поля , действующая на «пробный» заряд, равна векторной сумме сил, с которыми каждый из зарядовидействует в отсутствии другого на заряд(рис. 1.4). Отсюда и следует правило векторного сложения напряженностей электрических полей. Действительно, исходя из определения (1.3) напряженности электрического поля следует:

,

где и- напряженности полей одного из зарядов в отсутствии другого. Аналогичные рассуждения, конечно, можно провести не только для двух, но и для любого количества зарядов.

Пример 1.1. Определить потенциальную энергию взаимодействия двух точечных зарядов и.

Решение. Рассмотрим движение заряда в поле заряда. Пусть заряд, первоначально находившийся на расстоянииот зарядав точке с потенциалом, перемещается по произвольной траектории в точку с потенциалом, находящуюся на расстоянииот заряда. Тогда, согласно (1.7), работа электрического поля зарядапо перемещению зарядаравна:

.

Работа кулоновских сил, как сил потенциальных, не зависит от способа перемещения зарядов иотносительно друг друга и определяется выражением (1.8). Сравнение полученного результата и формулы (1.8) показывает, что потенциальная энергия взаимодействия двух точечных зарядов определяется выражением:

(1.15)

в предположении, что при бесконечно большом расстоянии между зарядами . Потенциальная энергия взаимодействия зарядов положительна, если заряды отталкиваются, и отрицательна, если заряды притягиваются.