
3.3. Анализ поляризованного света. Закон Малюса
а


Тот
факт, что кристалл (например турмалин)
дает возможность получить поляризованный
луч из естественного, говорит о том, что
в кристалле существуют определенные
плоскости «пропускания» вектора
![]() .
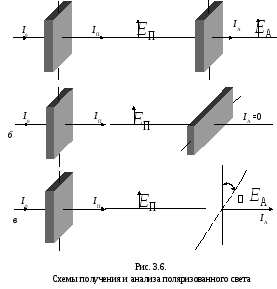
На рис.3.6
у поляризатора П
эти плоскости изображены в виде системы
параллельных линий (на рис.
3.6 плоскости
пропускания вектора
.
На рис.3.6
у поляризатора П
эти плоскости изображены в виде системы
параллельных линий (на рис.
3.6 плоскости
пропускания вектора
![]() параллельны плоскости чертежа).
параллельны плоскости чертежа).
Рассмотрим прохождение света через систему поляризатор анализатор. Пусть на поляризатор П падает естественный луч интенсивностью I. Из поляризатора, как было сказано ранее, выйдет плоскополяризованный свет с интенсивностью
![]() .
(3.3)
.
(3.3)
Для
исследования этого луча ставим на его
пути анализатор А.
При вращении
анализатора вокруг луча интенсивность
прошедшего через него света изменяется
от Imax
= IA
(рис. 3.6,
а)
до Imin
= 0
(рис.
3.6, б).
Если плоскости пропускания
![]() поляризатора
и анализатора параллельны друг другу,
то свет, выходящий из поляризатора,
полностью проходит через анализатор;
если плоскости пропускания анализатора
перпендикулярны плоскостям пропускания
поляризатора
(П
и А
скрещены), то свет через эту систему не
пройдет.
поляризатора
и анализатора параллельны друг другу,
то свет, выходящий из поляризатора,
полностью проходит через анализатор;
если плоскости пропускания анализатора
перпендикулярны плоскостям пропускания
поляризатора
(П
и А
скрещены), то свет через эту систему не
пройдет.
Расположение
направлений пропускания поляризатора
и анализатора, под некоторым углом
![]() ,
дает лишь частичную интенсивность света
на выходе из анализатора.
,
дает лишь частичную интенсивность света
на выходе из анализатора.
Пусть
![]()
амплитуда электрического вектора
плоскополяризованного света, вышедшего
из поляризатора (рис.
3.6, в).
На входе в анализатор этот свет разложится
на две волны, поляризованные соответственно
в плоскости пропускания анализатора
–
амплитуда электрического вектора
плоскополяризованного света, вышедшего
из поляризатора (рис.
3.6, в).
На входе в анализатор этот свет разложится
на две волны, поляризованные соответственно
в плоскости пропускания анализатора
–![]() и в перпендикулярной
ей плоскости
–
и в перпендикулярной
ей плоскости
–
![]() .
Амплитуды векторов
.
Амплитуды векторов ![]() и
и
![]() соответственно
равны:
соответственно
равны:
![]() ;
;
![]() .(3.4)
.(3.4)
Первая волна полностью пройдет через анализатор, а вторая поглотится в нем.
Так
как интенсивность света пропорциональна
квадрату амплитуды вектора |![]() |,
то интенсивность света, прошедшего
соответственно через анализатор и
поляризатор, запишется так:
|,
то интенсивность света, прошедшего
соответственно через анализатор и
поляризатор, запишется так:
![]() ;
;
![]() .
(3.5)
.
(3.5)
Соотношение
(3.5) носит
название закона Малюса:
интенсивность света, прошедшего через
анализатор
IA,
равна интенсивности света, прошедшего
через поляризатор
IП,
умноженной на квадрат косинуса угла
α между
плоскостями пропускания поляризатора
и анализатора.![]()
3.4. Интерференция поляризованного света
Явление поляризации света находит применение при анализе упругих напряжений, возникающих в деформированных деталях. Для этого изготавливают прозрачный шаблон детали и, подвергая его рабочим нагрузкам (сжатию, растяжению), помещают между поляризатором и анализатором. Изучая распределение интенсивности света после анализатора, получают сведения о напряжениях, возникающих в различных точках детали. В этом методе используется явление интерференции поляризованных лучей. Рассмотрим интерференцию поляризованных лучей.
Явление
интерференции возникает только в случае:
1) если лучи когерентны;
2) если
плоскость колебаний вектора
![]() у них одна
и та же (поляризованы в одной плоскости).
у них одна
и та же (поляризованы в одной плоскости).
Не
всегда два луча от одного и того же
источника света когерентны. Так,
обыкновенный и необыкновенный лучи,
возникающие при двойном лучепреломлении
из естественного света, некогерентны.
Это объясняется тем, что естественный
свет представляет собой набор
плоскополяризованных волн со всевозможными
ориентациями вектора
![]() относительно
луча. Эти элементарные волны соответствуют
излучениям независимых различных атомов
– источников
света, которые заведомо некогерентны
друг с другом. При расщеплении луча
естественного света на обыкновенный
и необыкновенный в среде распространяются
два луча, поляризованные во взаимно
перпендикулярных плоскостях. А так как
каждый атом испускает плоскополяризованную
волну, обыкновенный и необыкновенный
лучи образуются излучением разных
атомов и некогерентны.
относительно
луча. Эти элементарные волны соответствуют
излучениям независимых различных атомов
– источников
света, которые заведомо некогерентны
друг с другом. При расщеплении луча
естественного света на обыкновенный
и необыкновенный в среде распространяются
два луча, поляризованные во взаимно
перпендикулярных плоскостях. А так как
каждый атом испускает плоскополяризованную
волну, обыкновенный и необыкновенный
лучи образуются излучением разных
атомов и некогерентны.
Иначе обстоит дело, если на поляризатор падает поляризованный луч. Оказывается, что и в этом случае падающий свет претерпевает двойное лучепреломление. Но теперь обыкновенный и необыкновенный лучи когерентны, ибо рождаются одним и тем же атомом. Обыкновенный и необыкновенный лучи, возникающие из плоско-поляризованного света, когерентны.
Когерентные обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных плоскостях. При наложении двух когерентных лучей, поляризованных в двух взаимно перпендикулярных плоскостях, никакой интерференционной картины наблюдаться не будет. Интерференция возникает только в том случае, если колебания векторов Ē1 и Ē2 взаимодействующих лучей совершаются вдоль одного и того же направления. Колебания двух лучей, поляризованных первоначально во взаимно перпендикулярных направлениях, можно свести в одну плоскость, пропустив обыкновенный и необыкновенный лучи через анализатор. Анализатор устанавливают так, что его плоскость пропускания не совпадает с плоскостью колебаний этих лучей.
Еще в начале прошлого столетия было обнаружено, что оптически изотропное твердое тело под влиянием механической деформации становится оптически анизотропным. Например, при одностороннем сжатии или растяжении стеклянная пластинка приобретает свойства одноосного кристалла, оптическая ось которого совпадает с направлением сжатия или растяжения. Разность показателей преломления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси, пропорциональна нормальному напряжению σ
nо – nе = χ1 σ, (3.6)
где χ1 коэффициент, зависящий от свойств вещества.
Если прозрачную изотропную пластинку подвергнуть растяжению, то она приобретет свойства одноосного двоякопреломляющего кристалла. При размещении ее между поляризатором и анализатором, плоскости пропускания которых повернуты на угол α друг относительно друга, поляризованный луч претерпевает в ней двойное лучепреломление. В этом случае обыкновенный и необыкновенный лучи (о и е) распространяются внутри пластинки, не разделяясь, но с различой скоростью.
При прохождении через пластинку между лучами возникает оптическая разность хода
![]() ,
(3.7)
,
(3.7)
где d толщина пластинки.
Лучи
о
и
е,
поляризованные во взаимно перпендикулярных
плоскостях, падают на анализатор.
Колебания векторов
![]() и
и![]() лучей о
и е
после
прохождения через анализатор будут
лежать в одной плоскости. Следовательно,
эти два луча интерферируют с оптической
разностью хода ΔL
(формула
(3.7)).
лучей о
и е
после
прохождения через анализатор будут
лежать в одной плоскости. Следовательно,
эти два луча интерферируют с оптической
разностью хода ΔL
(формула
(3.7)).
