25

1. Интерференция света

1.1. Электромагнитная волна на границе раздела сред

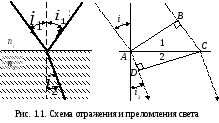
При прохождении электромагнитной волны через границу раздела сред происходит ее отражение и преломление.

Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раз­де­ла двух сред в точке падения. Угол падения равен углу отражения, (рис.1.1).

Закон преломления: луч пада­ю­щий, луч преломленный и перпендикуляр, про­ве­денный к границе раздела в точке падения, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред

, (1.1)

где n₂₁  относительный показатель преломления второй среды относительно первой.

Для установления причин преломления запишем для треугольников ABC и ACD (см. рис. 1.1) соотношения: ВС = AC sin i₁, AD = AC sin i₂, тогда отношение BC/AD = sin i₁/sin i₂. C учетом времени перехода фронта волны t и скоростей ее распространения v₁ и v₂ соответственно в средах 1 и 2 имеем BC = v₁t и AD = v₂t, откуда

. (1.2)

Таким образом, свет преломляется из-за различной скорости волн в разных средах. Абсолютный показатель преломления среды n показывает, во сколько раз скорость света в среде меньше, чем скорость света в вакууме: n = c/v.

В соответствии с электромагнитной природой скорость света и показатель преломления зависят от электромагнитных свойств среды (ее диэлектрической ₀ и магнитной ₀ проницаемости)

. (1.3)

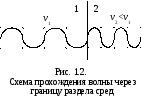
При прохождении волны через границу раздела сред (рис. 1.2) изменяется длина волны. Действительно, при v₂ < v₁ (v₁ = c) для первой среды с = , для второй среды v = , тогда

и .

На отрезки AD и BC (см. рис. 1.1) укладывается одно и то же количество волн.

Рассмотрим изменение плоской бегущей волны при переходе в другую среду. В вакууме

,

в среде

,

т.е. фаза волны зависит не от координаты x, а от оптической длины пути nx.

При отражении волны от границы раздела сред, когда волна проходит из оптически более плотной среды 1 в оптически менее плотную среду 2 (n₁ > n₂) оптическая разность хода двух лучей L = nx = = 0. При отражении от оптически более плотной среды (рис. 1.3) фаза скачком меняется на , а L  на /2, т.е. происходит потеря полуволны.

1.2. Интерференция света и условия её наблюдения. Когерентные источники света

При наложении волн в пространстве имеет место явление интерференции, заключающееся в том, что в одних местах волны усиливают друг друга, а в других ослабляют. Результаты такого сложения имеют общие закономерности независимо от природы волнового процесса.

Интерференцией света называется пространственное пере­распределение энергии светового излучения при наложении двух или нескольких световых волн, в результате чего в одних местах возникают максимумы (светлые пятна), а в других  минимумы (темные пятна) интенсивности света.

Повседневный опыт убеждает нас в том, что обычные источники света (например, лампочки накаливания) явления интерференции не дают. В чём причина этого? Какими должны быть источники световых волн, чтобы возникало явление интерференции?

Необходимым условием интерференции волн является их когерент­ность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Условию когерентности удовлетворяют монохроматические волны – неограниченные в пространстве волны одной определенной и строго постоянной частоты ( = const).

Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10^–8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τ вся совокупность излучающих атомов обновляется. Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ.

Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом. Средняя продолжительность одного цуга называется временем когерентности τ_ког. В соответствии с условием временной когерентности время когерентности не может превышать время излучения:

τ_ког< τ . (1.4)

При распространении волны фаза колебаний сохраняется только за время когерентности, за это время волна распространяется в вакууме на расстояние l_ког = сτ_ког – длины когерентности (длины цуга). Длина когерентности l_ког есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. В соответствии с условием пространственной когерентности оптическая разность хода не может превышать длину когерентности:

L < l_ког (1.5)

Волны, испускаемые двумя независимыми источ­никами света (даже двумя независимыми атомами), не когерентны, так как разность фаз между излучением этих источников хаотически изме­няется каждые 10^-8с. Это приводит к усреднению интенсивности в каждой точке пространства. Следовательно, некогерентные лучи не создают устойчивой, неизменной во времени интерференционной картины.

Более того, поскольку цуги волн, излучаемые одним и тем же атомом в разные моменты времени ( ∆ t > 10^-8 с), отличаются часто­той и фазой, то, очевидно, интерференция произойдет только при встрече волн, образуемых из одного и того же цуга.

Основная трудность в осуществлении явления интерференции све­та заключается в получении когерентных световых волн. Как было объяснено выше, для этого непригодны излучения не только двух различных макроскопических источников света (исключение состав­ляют лазеры), но и различных атомов одного и того же источника. Поэтому остается лишь одна возможность - каким-либо способом раз­делить свет, излучаемый каждым источником, на две группы волн, которые в силу общности происхождения должны быть когерентными и при наложении будут интерферировать. Отсюда все методы получения когерентных источников света сводятся к одной идее  разделению одного пучка от источника на две части и дальнейшему их сведению в одну точку. Практически это можно осуществить с помощью щелей (метод Юнга), зеркал (метод зеркал Френеля), преломляю­щих тел (метод бипризмы Френеля) и т.д.

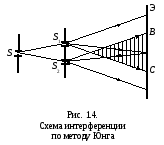
В качестве примера рассмотрим метод Юнга. Источником света служит ярко освещенная щель S (рис.1.1), от которой световая вол­на падает на две узкие равноудаленные щели S₁ и S₂, параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерент­ных источников. Интерференционная картина (область ВС) наблюда­ется на экране Э, расположенном на некотором расстоянии парал­лельно S₁ и S₂. Юнгу принадлежит первое наблюдение явления интерференции.

Интерференционная картина на экране (см. рис. 1.4) имеет вид полос, параллельных щели. Если источник S излучает монохромати­ческий свет (одного цвета  одинаковой частоты ν), то интерфе­ренционная картина представляет собой чередование светлых и тем­ных полос  это максимумы и минимумы интерференции.

От чего зависит результат интерференции в любой точке экрана? В каких случаях волны будут гасить друг друга, в каких – усиливать?

Рассмотрим два случая:

1) свет распространяется в вакууме (n₀ = 1);

2) свет распространяется в средах с разными показателями пре­ломления (n₁ ≠ n₂ ≠ 1).

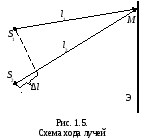
1. Пусть оба когерентных луча от источников S₁ и S₂ про­ходят пути l₁ и l₂ до встречи в т. М экрана в вакууме (рис. 1.5). В этой случае l₁ и l₂ - геометрические пути лучей. Рассчитаем резуль­тат наложения двух синусоидальных когерентных волн в произвольной точке M экрана. Сделаем это для электрического вектора (не следует забывать о том, что в однородной среде интенсивность света пропорциональна квадрату амплитуды вектора напряженности I ≈ E²).

Колебания, приходящие в точку М от источников S₁ и S₂, опи­сываются уравнениями:

,

(1.6)

,

где λ₀  длина волны в вакууме.

По принципу суперпозиции волн ам­плитуда результирующего колебания в т. М определяется формулой

(1.7)

для интенсивностей

,

где и  (1.8)

фазы складываемых колебаний.

Из выражения (1.7) следует, что величина амплитуды результиру­ющего колебания Е₀, а, значит и интенсивности, зависит только от разности фаз (φ₁–φ₂) складываемых колебаний.

Итак, волны называются когерентными, если в произволь­ной точке их встречи разность фаз колебаний остается постоянной во времени.

При этом возможны два предельных ва­рианта.

а) (φ₁  φ₂) = ±2kπ (k = 0, 1, 2, ...), (1.9)

cos (φ₁ – φ₂) = 1; Е₀ = Е₀₁ + Е₀₂ ; ,

т.е. амплитуда и интенсивность результирующего колебания максимальна (в случае E₀₁=E₀₂ E₀ =2E_01,, a I = 4I₀₁).

Из уравнений (1.6) находим разность фаз

, (1.10)

где Δl = (l₂ – l₁ )  геометрическая разность хода волн от источников S₁ и S₂ до т. M экрана (см. рис. 1.5).

Из фор­мул (1.9) и (1.10) следует, что условие интерференционного максимума

, (1.11)

где k  порядок интерференционного максиму­ма (k = 0, 1, 2, …, при k = 0 наблюдают максимум в центре экрана).

б) (φ₁ – φ₂) = ± (2k + 1)π (k = 0, 1, 2, ...), (1.12)

cos (φ₁ – φ₂) = – 1; Е₀ = Е₀₁ – Е₀₂ ; ,

т.е. амплитуда результирующего колебания, а, следовательно, и интенсивность – минимальна (в случае E₀₁= E₀₂ E₀ = 0 и I = 0).

Из формул (1.10) и (1.11) следует условие интерференционного минимума

, (1.13)

где k – порядок интерференци­онного минимума.

2. Если когерентные лучи проходят свои пути до точки М в раз­ных средах: первый – путь l₁ в среде с показателем преломления п₁ , второй – путь l₂, в среде с показателем преломления n₂, то условия образования максимумов и минимумов интерференции бу­дут зависеть не от геометрической разности хода Δl = (l₂ – l₁ ), а от оптической разности хода

ΔL = L₂ – L₁ = l₂n₂ – l₁n₁, (1.14)

где L₁, и L₂ – оптические пути лучей 1 и 2, L₁= l₁ п₁; L₂= l₂n₂. В этом случае разность фаз складываемых волн

, (1.15)

где с – скорость света в вакууме, v – скорость света в среде; λ – длина волны, λ = v/;  – частота. Для вакуума λ₀ = с/, а для среды с показателем преломления n λ = λ₀/n.

Приравняв поочередно (1.11) и (1.12) к (1.15), получим условие ин­терференционных максимумов:

, (1.16)

и интерференционных минимумов:

, (1.17)

где k = 0, 1, 2, 3, … .

Итак, в тех местах на экране, до которых в оптической разно­сти хода лучей укладывается четное число полуволн, колебания, приходящие от обоих источников, складываются, амплитуда удваива­ется, а интенсивность возрастает в 4 раза. В тех местах экрана, до которых в оптичес­кой разности хода укладывается нечетное число полуволн, колеба­ния приходят в противоположной фазе и полностью гасят друг друга.

П р и м е ч а н и я:

1. Из формулы (1.15) обнаруживается связь между разностью фаз и оптической разностью хода:

.

2. Монохроматическим называют излучение одной длины волны λ = соnst (точнее узкого интервала длин волн). Такой свет воспринимается как одноцветный. Белый свет представлен набором длин волн от фиолетового до красного. Если источник S излучает свет не монохроматический, а белый, то интерфе­ренционные максимумы имеют вид радужных полос (кроме центрального максимума, где k = 0). Это объясняется тем, что условие максиму­ма интерференции (1.16) для данной длины волны выполняется только в определенной точке экрана. Поэтому белый свет в резуль­тате интерференции разлагается в интерференционный спектр. В цент­ре интерференционной картины, где k = 0, результат интерференции не зависит от длины волны λ .

Результат расчета интерференционной картины от двух когерентных источни­ков можно привести на примере опыта Юнга. Щели S₁ и S₂ (рис. 1.6) находятся на расстоянии d друг от друга и являются когерентными источниками света. Интерференция наблюдается в произвольной точке M экрана, расположенного параллельно обеим щелям на расстоянии L , причем L >> d . Начало отсчета выбрано в т. О экрана, расположенной симметрично относительно щелей S₁ и S₂ .

Интенсивность в любой точке М экрана, лежащей на расстоянии х от точки 0, определяется разностью хода Δ l = l₂  l₁ ( см. рис. 1.6).

Максимумы интен­сивности будут наблюдаться при

x_max = ± kLλ₀/d (k = 0, 1, 2, ...), (1.18)

минимумы интенсивности – при

x_min = ±(2k+1)Lλ₀/2d (k = 0, 1, 2, ...). (1.19)

Расстояние между двумя соседними максимумами или минимумами, называемое шириной интерференционной полосы,

Δx = Lλ₀/d . (1.20)

Из формулы (1.20) видно, что ширина интерференционной полосы Δх не зависит от порядка интерференции (величины k) и является постоянной для данных L , d. и λ₀ . По измеренным значениям L , d. и λ₀ , используя (1.20), можно экспериментально опреде­лить длину световой волны λ₀ .