Поток напряженности электрического поля.

Пусть в некоторой области пространства известно векторное поле напряженности электростатического поля . Допустим, что в окрестности фиксированной точки пространства имеется элемент поверхности площади , ориентацию которого можно задать с помощью вектора единичной (безразмерной) нормали к этому элементу поверхности. Поскольку элемент поверхности является двусторонним объектом, то направление нормали можно выбрать произвольно. Введем в рассмотрение объект

,

(2.8)

     вектор элемента площади поверхности. В соответствии с (2.8) этот вектор численно равен площади элемента поверхности, имеет размерность площади и направлен вдоль , то есть вдоль нормали к элементу поверхности.

      Элемент потока вектора через площадку по определению равен скалярному произведению вектора и вектора :

.	(2.9)
Рис. 1.6. Элементарный поток вектора напряженности электростатического поля

     Угол в выражении (2.9) измеряется между направлением вектора и направлением нормали к площадке . При , то есть при , значение элемента потока вектора максимально, а при элемент потока обращается в нуль. Это свойство элемента потока легко понять, если привлечь понятие силовой линии векторного поля. В первом случае силовые линии перпендинулярны площадке , а во втором случае они "скользят" вдоль площадки, не пересекая ее. Заметим, что , если угол - тупой.       Если рассматривать поверхность конечных (или бесконечных) размеров, то можно определить поток вектора через эту поверхность:

.

(2.10)

Здесь вектор направленный по нормали к поверхности.

Если напряженность электрического поля создается системой нескольких зарядов, то из принципа суперпозиции можно представить поле , а следовательно и поток как:

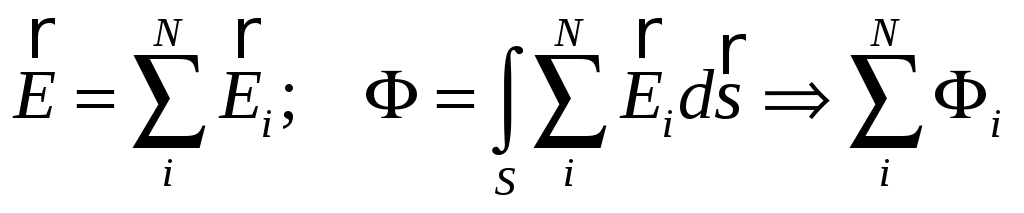
Таким образом, поток напряженности электрического поля через произвольную поверхность от системы электрических зарядов равен сумме потоков напряженности электрического поля создаваемого независимо каждым зарядом в отдельности

В определении подразумевается, что поверхность достаточно гладкая, направления нормалей к двум соседним элементам поверхности не сильно различаются между собой. Последнее означает, что все элементы поверхности построены "на одной стороне" поверхности.

Если поверхность является замкнутой поверхностью, то, как правило, поток вектора через поверхность рассчитывают с использованием внешней нормали по отношению к объему, заключенному внутри поверхности :

,

(2.11)

     где кружок у интеграла означает, что поверхность - замкнутая.

Теорема Гаусса

      Поток вектора напряженности электростатического поля через замкнутую поверхность обладает специфическим свойством: его величина пропорциональна электрическому заряду, расположенному внутри этой поверхности. Это утверждение составляет физический смысл теоремы Гаусса. Теорема Гаусса для вектора напряженности электростатического поля в вакууме является следствием закона Кулона. Теорема Гаусса имеет большое значение в теории электромагнетизма.

Допустим, что в начале координат помещен точечный электрический заряд . Окружим этот заряд произвольной замкнутой поверхностью. Затем окружим эту поверхность сферой радиуса r, так, чтобы заряд был в центре сферы

 

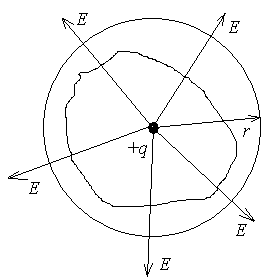
Рис.2.4.

Электрический заряд, окруженный произвольной поверхностью

     Напряженность электрического поля, созданного этим зарядом, описывается соотношением:

,

(2.12)

     где - радиус-вектор точки наблюдения, - его модуль. Известно, что внешняя нормаль к элементу поверхности сферы направлена по радиусу:

.

(2.13)

     Поток вектора через нашу произвольную замкнутую поверхность равен потоку через поверхность сферы и равен:

.

(2.14)

Реальное электростатическое поле обусловлено совокупностью точечных зарядов (принцип суперпозиции), для каждого из которых соотношение

(2.15)

     доказано для произвольной замкнутой поверхности . Но тем самым доказана справедливость теоремы Гаусса для произвольного электростатического поля: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен суммарному электрическому заряду, находящемуся внутри поверхности , деленному на величину .

      Заметим, что соотношение (2.15) справедливо для системы единиц СИ.

      То обстоятельство, что замкнутая поверхность в формулировке теоремы Гаусса может быть произвольной, позволяет выбрать ее форму при решении конкретной задачи удобным для исследователя способом.

      Использование теоремы Гаусса в интегральной форме (2.15) в отдельных случаях, отличающихся высокой степенью симметрии расположения электрических зарядов в пространстве, позволяет эффективно рассчитывать характеристики электростатического поля.

      В общем случае теорема Гаусса в форме (2.15) может служить для получения оценок характерных величин электростатического поля.

      Теорема Гаусса для вектора напряженности электростатического поля может быть сформулирована и в дифференциальной форме, отражающей локальные свойства электростатического поля.

Теорема Гаусса для вектора напряженности электростатического поля может быть сформулирована и в дифференциальной форме, отражающей локальные свойства электростатического поля.

      Действительно, рассмотрим поле точечного электрического заряда , расположенного в начале координат:

.

(2.16)

     Из соотношения (2.16) следует

     

(2.17)

     Легко проверить, что для , то есть для точки наблюдения, в которой нет электрического заряда, справедливо соотношение:

.

(2.18)

     Математическая операция в левой части соотношения (2.18) имеет специальное название "дивергенция векторного поля " и специальное обозначение

.

(2.19)

     Очевидно, что результат (2.15) можно записать в форме:

.

(2.20)

     Нетрудно сообразить, что формула (2.20) будет иметь силу и для произвольного электростатического поля в каждой точке, где отсутствует электрический заряд.      Если в окрестности начала координат имеется объемная плотность электрического заряда и рассматриваются расстояния от начала координат настолько малые, что величину можно считать постоянной величиной, то напряженность электростатического поля в окрестности начала координат может быть определена соотношением:

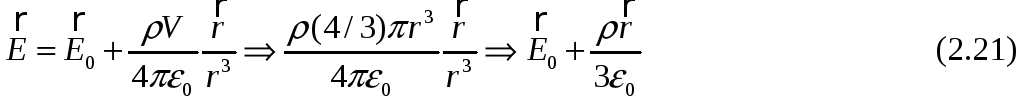
 где - напряженность электрического поля, создаваемого зарядами вне рассматриваемой окрестности, - векторная постоянная величина. В проекциях на оси декартовой системы координат имеем:

.

(2.22)

     Вычисляя дивергенцию векторного поля (2.21) - (2.22), получаем

.

(2.23)

     При из соотношения (2.23) следует соотношение (2.20).

      Соотношение (2.23) является дифференциальной формулировкой теоремы Гаусса для векторного поля . Заметим, что дифференциальная формулировка теоремы Гаусса для векторного поля (2.23) непосредственно следует из интегральной формулировки (2.15).

      Действительно, в силу математической теоремы Остроградского-Гаусса имеет место соотношение

,

(2.24)

     где - объем, ограниченный замкнутой поверхностью . Если при этом величина электрического заряда в объеме может быть записана в форме

,

(2.25)

     то из формулировки (2.15), теоремы (2.24) и формулы (2.25) следует

.

(2.26)

     Поскольку соотношение (2.26) должно выполняться для произвольного объема (не только какого-либо конкретного), то единственной возможностью выполнения условия (2.26) является обращение в нуль подынтегрального выражения, что приводит к соотношению (2.23). Выше было сказано, что эффективность применения теоремы Гаусса для векторного поля существенно зависит от степени симметрии пространственного заряда. При этом речь шла об интегральной формулировке теоремы (2.15). Аналогичное явление имеет место и при рассмотрении дифференциальной формулировки теоремы Гаусса (2.23): она не является самодостаточной, поскольку соотношением (2.23) связаны между собой три функции - , а уравнение всего одно единственное. Понятно, что только при наложении дополнительных связей между этими функциями можно будет определить каждую из них.
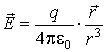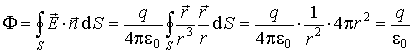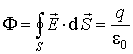
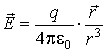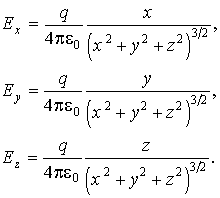
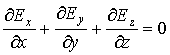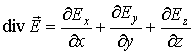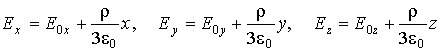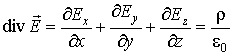