11. Характеристики ремонтопригодности.

Рассмотрим систему длительного (многократного) использования. В этом случае система после отказа восстанавливается и затем продолжает функционировать.

Время восстановления системы 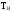- суммарное время обнаружения и устранения отказов.

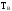зависит от многих факторов, имеющих случайный характер (вид отказа, тип и число отказавших элементов).

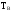- случайная величина.

Ремонтопригодность системы характеризуется следующими вероятностными характеристиками:

1. вероятность выполнения ремонта в заданное время ;

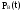2. вероятность невыполнения ремонта в заданное время ;

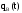3. плотность вероятности времени восстановления ;

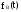4. интенсивность восстановления ;

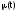5. среднее время восстановления ;

6. дисперсия времени восстановления .

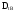Вероятность выполнения ремонта в заданное время - это вероятность того, что отказ изделия будет устранён в течении заданного t

.

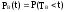Вероятность невыполнения ремонта в заданное время - это вероятность того, что отказ изделия не будет устранён в течении заданного времени t

.

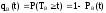Плотность вероятности времени восстановления 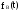равна

.

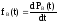Интенсивность восстановления 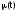равна:

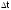
0

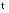
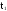
Событие А - отказ изделия не устранён на интервале времени от 0 до t.

Событие В - отказ изделия не устранён на интервале времени от 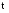до .

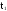АВ - произведение событий А и В. Произведением событий А и В является событие, заключающееся в совместном появлении этих событий

P(AB) = P(A) P(B/A).

P(B/A) - условная вероятность события В при условии, что событие А произошло (имело место).

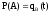- вероятность того, что отказ изделия не устранён на интервале времени от 0 до t.

P(B/A) = P(AB) / P(A).

Вероятность P(AB) есть вероятность того, что отказ изделия не устранён на интервале

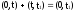
т.е. P(AB) =

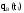
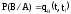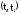- вероятность того, что отказ изделия не устранён на интервале времени при условии, что отказ изделия не был устранён на интервале времени от 0 до t.

Таким образом

;

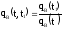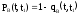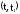- вероятность того, что отказ изделия будет устранён на интервале времени при условии, что отказ изделия не был устранён на интервале времени от 0 до t.

.

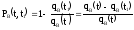Пусть 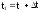; тогда

;

;

;

.

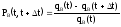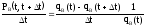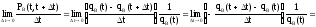
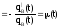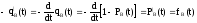Таким образом: ; (*)

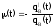или:

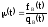
Из (*) имеем ;

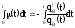или ;

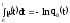или ;

;

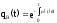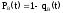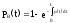
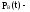вероятность выполнения ремонта в заданное время.

При 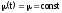получаем экспоненциальный закон ремонтопригодности

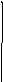
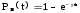
1

0 t

Определим среднее время восстановления :

;

;

;

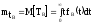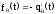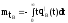Это интеграл можно вычислить по частям

u = t; ;

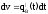du = dt; ;

;

;

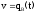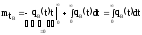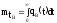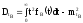-дисперсия времени восстановления

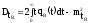
В случае экспоненциального закона ремонтопригодности имеем:

; .
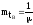
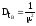