
- •Надёжность неремонтируемых изделий.
- •Проблемы надёжности.
- •Факторы, влияющие на надёжность при проектировании.
- •1.2.2 Факторы, влияющие на надёжность в процессе изготовления.
- •Пути повышения надёжности.
- •Основные понятия теории надёжности.
- •Виды надёжности.
- •Основные понятия и теоремы теории вероятностей.
- •Классификация событий.
- •Теорема сложения вероятностей.
- •Теорема умножения вероятностей.
- •Теорема полной вероятности.
- •Количественные характеристики надёжности.
- •1.9 Интенсивность отказов (t).
- •Определение интенсивности отказов (t) по результатам испытаний.
- •Числовые характеристики надёжности.
- •Характеристики ремонтопригодности.
- •Экспериментальная оценка надёжности изделий.
- •Выравнивание статистического закона распределения случайной величины т.
- •Критерий Пирсона.
- •Критерий Колмогорова.
- •Законы распределения отказов и их основные характеристики.
- •Экспоненциальный закон надёжности.
- •Нормальный закон распределения.
- •Закон распределения Вейбулла.
- •Виды соединения элементов в систему.
- •Последовательное соединение элементов в систему.
- •Паралельное соединение элементов в систему.
- •Классификация методов резервирования.
- •Расчёт надёжности системы с постоянным резервированием.
- •Расчёт надёжности системы с постоянным общим резервированием.
- •Расчёт надёжности системы с постоянным поэлементным резервированием.
- •Режим облегченного (тёплого) резерва.
- •Режим нагруженного резерва.
- •Режим ненагруженного резерва.
- •2. Надёжность ремонтируемых (восстанавливаемых) изделий.
- •Надёжность системы с восстановлением.
- •Надёжность программного обеспечения.
- •Сравнительные характеристики программных и аппаратурных отказов.
- •Проверка и испытания программ.
- •Основные проблемы исследования надёжности программного обеспечения.
- •Критерии оценки надёжности программных изделий.
- •Критерии надёжности сложных комплексов программ.
- •Математические модели надёжности комплексов программ.
- •Проверка математических моделей.
-
Количественные характеристики надёжности.
Предварительно рассмотрим понятие “случайная величина”.
Случайная величина - величина, которая в результате опыта может принять то или иное значение, причём заранее неизвестно, какое именно.
Примеры случайной величины:
-
Интервал времени между соседними отказами ЭВМ;
-
Интервал времени от начала работы изделия до первого отказа или время безотказной работы;
-
Число деталей, изготовленных рабочим в единицу времени.
Обозначим через T - время безотказной работы изделия (интервал времени от начала работы изделия до первого отказа). T - случайная величина. Величина T также называется наработка на отказ изделия. t - возможные значения случайной величины T.
Введём понятие “вероятность безотказной работы”.
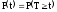 -
вероятность того, что время безотказной
работы изделия будет
больше или равно некоторому значению
t.
Другими словами, вероятностью безотказной
работы называется вероятность того,
что при заданных условиях эксплуатации
в течении интервала времени t
не возникнет отказа, т.е.система будет
работоспособна.
-
вероятность того, что время безотказной
работы изделия будет
больше или равно некоторому значению
t.
Другими словами, вероятностью безотказной
работы называется вероятность того,
что при заданных условиях эксплуатации
в течении интервала времени t
не возникнет отказа, т.е.система будет
работоспособна.
Вероятность отказа:
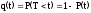
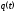 -
вероятность
того, что время безотказной работы
изделия меньше некоторого заданного
значения t.
-
вероятность
того, что время безотказной работы
изделия меньше некоторого заданного
значения t.
Другими словами, вероятностью отказа является вероятность того, что в течении заданного времени произойдёт хотя бы один отказ.
Функция
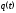 представляет
собой функцию распределения случайной
величины Т.
представляет
собой функцию распределения случайной
величины Т.
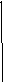
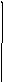 q(t)
p(t)
q(t)
p(t)
0 P(t) 1;

 1
1
P(0) = 1; P()
= 0;
1
1
P(0) = 1; P()
= 0;

 0
t 0
t
0
t 0
t
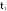
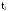




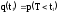 ;
;
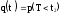 .
.
0
 T
T
Рассмотрим события А, В, С.




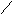
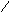
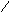
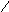
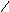




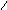

 Событие
А:
Событие
А:
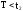 ;
0
T
;
0
T
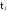
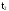



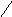
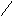
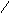
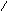
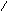
 Событие
В:
Событие
В:
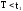 ;
0
T
;
0
T
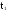
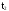











 Событие
С:
Событие
С:
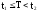 ;
0
T
;
0
T
События В и С несовместные события (в опыте не могут появиться вместе).
А = В + С; P(A) = P(B) + P(С);
откуда
P(С)
= P(A) - P(B); P(A) =
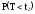 ;
P(B) =
;
P(B) =
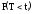 ;
;
P(C)
=
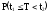 ;
;
Следовательно
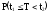 =
=
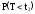 -
-
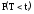 ;
;
или
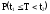 =
=
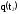 -
-
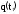 ;
;
Введём
в рассмотрение событие А. Событие А
означает, что
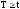 ,
т.е. в интервале времени от 0 до t
отказа
не произойдёт.
,
т.е. в интервале времени от 0 до t
отказа
не произойдёт.
Введём
в рассмотрение событие
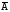 .
Событие
.
Событие
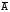 означает, что T
<
t
,
т.е в интервале времени от 0 до t
произойдёт
отказ. События A
и
означает, что T
<
t
,
т.е в интервале времени от 0 до t
произойдёт
отказ. События A
и
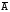 являются противоположными, т.к. они
образуют полную группу событий. События
образуют полную группу, если в результате
опыта одно из них обязательно должно
произойти.
являются противоположными, т.к. они
образуют полную группу событий. События
образуют полную группу, если в результате
опыта одно из них обязательно должно
произойти.
Из теории вероятностей известно, что сумма вероятностей противоположных событий равна единице, т.е.
P(A)
+ P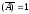 ;
;
P(A)
= P(T
t) ; P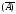 =
P(T<t) ;
=
P(T<t) ;
Следовательно P(T t) + P(T < t) = 1 или



P(t) + q(t) = 1

Для вероятности безотказной работы справедливо приближённое соотношение
P(t)
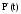 ,
где
,
где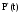 =
=
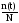
Здесь n(t) - число изделий, не отказавших к моменту времени t;
N - число изделий, поставленных на испытания.
Испытания изделий должны проводиться при одинаковых условиях так, чтобы отказы изделий были независимы друг от друга.
Для вероятности отказа справедливо приближённое равенство
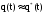 ;
где
;
где
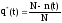 .
.
Здесь N - n(t) - число изделий, отказавших к моменту времени t.
-
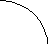
Плотность вероятности f(t) времени безотказной работы T.
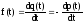 ;
;
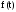 -
частота
отказов.
-
частота
отказов.
Здесь
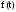 -
плотность
вероятности случайной величины T
или частота отказов.
-
плотность
вероятности случайной величины T
или частота отказов.
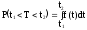 вероятность
того, что отказ изделия произойдёт на
интервале времени
вероятность
того, что отказ изделия произойдёт на
интервале времени
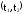 .
.

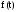
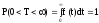 ;
;



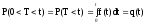 ;
;



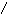
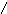
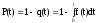 ;
;
0 t
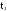
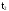
Для плотности вероятности времени безотказной работы T справедливо приближённое равенство:
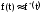 ,
где
,
где
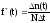 - оценка частоты отказов.
- оценка частоты отказов.
Здесь
N
- число изделий, поставленных на испытания,
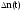 - число отказавших изделий на участке
времени (t,
t
+ t).
- число отказавших изделий на участке
времени (t,
t
+ t).



 0
t t + t
T
0
t t + t
T
