- •Надёжность неремонтируемых изделий.
- •Проблемы надёжности.
- •Факторы, влияющие на надёжность при проектировании.
- •1.2.2 Факторы, влияющие на надёжность в процессе изготовления.
- •Пути повышения надёжности.
- •Основные понятия теории надёжности.
- •Виды надёжности.
- •Основные понятия и теоремы теории вероятностей.
- •Классификация событий.
- •Теорема сложения вероятностей.
- •Теорема умножения вероятностей.
- •Теорема полной вероятности.
- •Количественные характеристики надёжности.
- •1.9 Интенсивность отказов (t).
- •Определение интенсивности отказов (t) по результатам испытаний.
- •Числовые характеристики надёжности.
- •Характеристики ремонтопригодности.
- •Экспериментальная оценка надёжности изделий.
- •Выравнивание статистического закона распределения случайной величины т.
- •Критерий Пирсона.
- •Критерий Колмогорова.
- •Законы распределения отказов и их основные характеристики.
- •Экспоненциальный закон надёжности.
- •Нормальный закон распределения.
- •Закон распределения Вейбулла.
- •Виды соединения элементов в систему.
- •Последовательное соединение элементов в систему.
- •Паралельное соединение элементов в систему.
- •Классификация методов резервирования.
- •Расчёт надёжности системы с постоянным резервированием.
- •Расчёт надёжности системы с постоянным общим резервированием.
- •Расчёт надёжности системы с постоянным поэлементным резервированием.
- •Режим облегченного (тёплого) резерва.
- •Режим нагруженного резерва.
- •Режим ненагруженного резерва.
- •2. Надёжность ремонтируемых (восстанавливаемых) изделий.
- •Надёжность системы с восстановлением.
- •Надёжность программного обеспечения.
- •Сравнительные характеристики программных и аппаратурных отказов.
- •Проверка и испытания программ.
- •Основные проблемы исследования надёжности программного обеспечения.
- •Критерии оценки надёжности программных изделий.
- •Критерии надёжности сложных комплексов программ.
- •Математические модели надёжности комплексов программ.
- •Проверка математических моделей.
-
Расчёт надёжности системы с постоянным поэлементным резервированием.
При поэлементном резервировании резервируются отдельно элементы системы.










 Э10
Э20 Эi0
Эn0
Э10
Э20 Эi0
Эn0






 Э11
Э21
Эi1
Эn1
Э11
Э21
Эi1
Эn1

 ……………………………………………………………
……………………………………………………………






 Э1j
Э2j
Эij
Эnj
Э1j
Э2j
Эij
Эnj
……………………………………………………………






 Э1m
Э2m
Эim
Эnm
Э1m
Э2m
Эim
Эnm

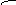

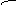

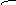

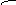








1-я группа 2-я группа i - я группа n - я группа
Определим количественные характеристики надёжности системы.
Введём обозначения:
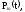 i = 1,
2, ……..,n
-
вероятность безотказной работы элемента
Эio
на интервале времени (0, t);
i = 1,
2, ……..,n
-
вероятность безотказной работы элемента
Эio
на интервале времени (0, t);
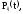 j = 1,
2, ……..,m; i = 1, 2, …….,n - вероятность
безотказной работы элемента
Эij
на интервале времени (0, t).
j = 1,
2, ……..,m; i = 1, 2, …….,n - вероятность
безотказной работы элемента
Эij
на интервале времени (0, t).
Запишем вероятность отказа i - й группы.
Имеем
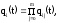 i
=
1, 2, …….,n.
i
=
1, 2, …….,n.
Запишем вероятность безотказной работы i - ой группы. Имеем
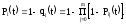
Запишем вероятность безотказной работы системы с поэлементным резервированием




 или
или
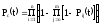
Для равнонадёжных элементов системы имеем:
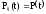
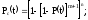
-
Режим облегченного (тёплого) резерва.
Рассмотрим случай, когда время безотказной работы всех элементов изделия подчиняется экспоненциальному закону распределения. В этом случае процессы, характеризующие работу изделия являются марковскими. Для определения характеристик надёжности можно использовать математический аппарат теории марковских случайных процессов.
В режиме облегченного резерва резервные элементы находятся в режиме недогрузки до момента их включения в работу. Пусть 1 - интенсивность отказа резервного элемента в режиме недогрузки до момента их включения в работу. 0 - интенсивность отказа резервного элемента в состоянии работы.
Введём
в рассмотрение состояния
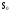 ,
,
S0 - основной элемент исправен и работает, m резервных элементов исправны и находятся в режиме недогрузки.
S1 - основной элемент отказал, работает 1 - ый резервный элемент, (m - 1) резервные элементы исправны и находятся в режиме недогрузки.
S2 - отказал 1 - ый резервный элемент, работает 2 - ой резервный элемент, (m - 2) резервных элементов исправны и находятся в режиме недогрузки.
Si - отказал i - й резервный элемент, работает i - й резервный элемент, (m - i ) резервных элементов исправны и находятся в режиме недогрузки.
Sm - отказал (m - 1) - ый элемент, работает m - ый резервный элемент.
Sm+1 - отказал m -ый резервный элемент.
Построим граф состояний:



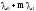
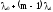 …….
…….
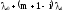
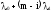 0
0





 S0
S1
Si
Sm+1
S0
S1
Si
Sm+1
Запишем систему дифференциальных уравнений Колмогорова. Для этого введём обозначения:
P0(t) - вероятность нахождения резервированной системы в момент времени t в состоянии S0.
Pi(t) - вероятность нахождения резервированной системы в момент времени t в состоянии Si , i = 0, 1, ….., m, m + 1.


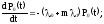
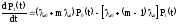 ;
;
 ………………………………………………….
………………………………………………….


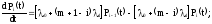
………………………………………………….

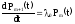 .
.
Начальные условия:
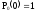
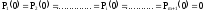 .
.
Применим к системе дифференциальных уравнений Колмогорова преобразование Лапласа. Получим систему линейных алгебраических уравнений вида: Pi(t) - оригинал
Pi(S) - изображение по Лапласу
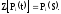
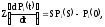 i
=
0, 1, ……,
m
+1
i
=
0, 1, ……,
m
+1



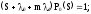
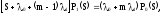


 …………………………………………….
…………………………………………….
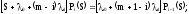
…………………………………………….
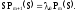
Решая систему уравнений получим
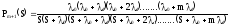
Найдём
оригинал
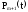 .
Имеем
.
Имеем
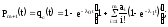
где
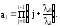
Здесь
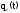 -
вероятность отказа резервированной
системы с облегченным резервированием.
-
вероятность отказа резервированной
системы с облегченным резервированием.
Определим вероятность безотказной работы системы с облегченным резервированием. Имеем:
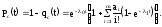
Определим среднее время безотказной работы системы с облегченным резервированием. Имеем:
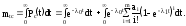
Формула бинома Ньютона
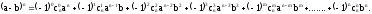 где
где
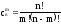
При a = 1 имеем:
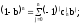
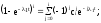
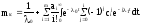
Выполнив преобразование, получим:



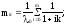 где
где
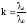 .
.

Определим
частоту отказов
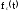 резервированной системы. Имеем
резервированной системы. Имеем
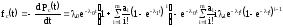 ;
;



или
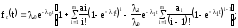

Определим
интенсивность отказов
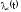 резервированной системы. Имеем
резервированной системы. Имеем