-
Расчёт надёжности системы с постоянным резервированием.
При
постоянном резервировании резервные
элементы 1,2,…..,m
0
соединены паралельно с
основным (рабочим) элементом в тече-
нии всего периода работы системы. Все элементы соединены
постоянно,
перестройка схемы при отказах не
происходит, отка-
1
завший элемент не
отключается.
………..
m
Определим вероятность отказа системы.
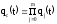
Вероятность безотказной работы системы.
.
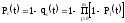Будем называть элементы системы равнонадёжными, если
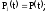j = 0, 1,
……, m
Для равнонадёжных элементов имеем
.
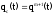
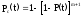При экспоненциальном законе надёжности отдельных элементов имеем
.
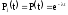Тогда
;
.
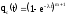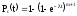Определим среднее время безотказной работы резервированной системы
.
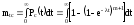Введём
новую переменную x
вида
;
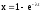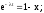
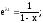
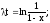
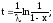
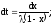
Если t = 0, то x = 0;
Если t = , то x = 1;
В результате получим
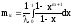
Запишем формулу для определения суммы n членов геометрической прогрессии
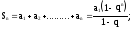
где
-
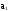первый член суммы;
-
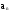n
- ый член суммы;
q
-
знаменатель прогрессии;
(
);
.
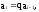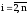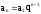Выражение
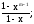
есть
сумма n
членов геометрической прогрессии, где
q
= x; n = m + 1;
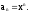
Следовательно
;
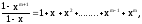
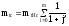
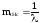где
-
среднее время безотказной работы
нерезервированной системы. Введём
обозначение
;
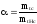Для разных значений m имеем
m = 0; = 1;
m = 1; = 1,5;
m = 2; = 1,83.
Результаты сведём в таблицу
m
m
0
1 8
2,826
1
1,5 9
2,926
2
1,83 10
3,017
3
2,08 11
3,1
4
2,28 12
3,177
5
2,446 13
3,248
6
2,59 14
3,315
7
2,715 15
3,38
По данным таблицы строим график зависимости от m.
График имеет вид:
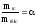
4
3
2
1
m
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15