17. Виды соединения элементов в систему.

1. Последовательное соединение.

2. Паралельное соединение.

1. Последовательное соединение элементов в систему.

1 2 i n

Соединение элементов называется последовательным, если отказ хотя бы одного элемента приводит к отказу всей системы. Система последовательно соединённых элементов работоспособна тогда, когда работоспособны все её элементы.

Рассчитаем надёжность системы при последовательном соединении элементов в систему. Рассчитать надёжность системы - это значит по заданным количественным характеристикам надёжности элементов определить количественные характеристики надёжности системы.

Рассмотрим события 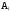, i = 1, 2, ……….,n.

Событие 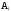означает безотказную работу элемента i за время t.

Считаем, что события 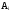независимые, т.е. вероятность события 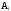P(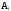) не зависит от события 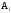, j  i.

В этом случае элементы системы называются независимыми в смысле надёжности.

Рассмотрим событие А.

Событие А означает безотказную работу системы из n последовательно соединённых элементов за время t.

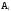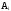Событие А имеет место, если одновременно выполняются события , i = 1, 2, ……….,n. Следовательно событие А равно произведению событий , т.е.

….

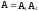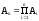
Из теории вероятностей известно, что в этом случае

……...

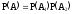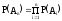Обозначим 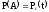- вероятность безотказной работы системы за время t.

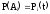- вероятность безотказной работы i - го элемента за время t.

Откуда ……….

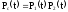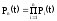Т.о., вероятность безотказной работы системы за время t равна произведению вероятностей безотказной работы за время t элементов системы.

В частном случае, когда все элементы системы одинаковы, имеем

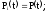
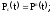
Выразим вероятность безотказной работы элементов 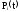через их интенсивность отказов

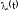. Имеем

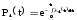; i = 1, 2, …, n

Запишем формулы для определения вероятности безотказной работы системы 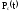. Имеем

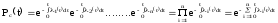
или

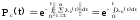
где

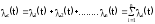
Здесь 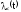- интенсивность отказов системы.

Т.о., при последовательном соединении элементов их интенсивность отказов складывается и интенсивность отказов системы есть сумма интенсивностей отказов элементов системы.

Вероятность отказа системы на интервале времени (0, t) равна

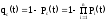
или

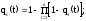
Интенсивность отказов 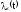системы

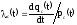
Среднее время безотказной работы системы

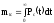
В случае экспоненциального закона надёжности всех элементов имеем:

;

; ;

;

;

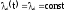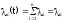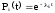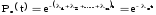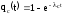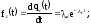
Т.о. закон распределения времени безотказной работы системы является экспоненциальным.

Определим среднее время безотказной работы системы. Имеем

;
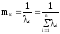