7.4. Определение перемещений способом Верещагина

Для конструкций, состоящих из прямолинейных стержней с постоянным поперечным участком на i-м участке, интегралы Мора удобно вычислять по формуле Верещагина:

. (7.14)

Рассматриваемый подход представляет собою графоаналитический способ. В формуле (7.14) – площадь эпюры грузового силового фактора;– значение ординаты единичного силового фактора под центром тяжести площади;– число площадей. Перемещения по способу Верещагина определяют следующим образом.

1. Строят эпюру изгибающих моментов для заданной системы от внешней нагрузки.

2. Составляют схему единичного загружения и строят эпюру изгибающих моментов от единичной нагрузки .

3. Разбивают эпюры и наn одинаковых участков так, чтобы выполнялись следующие условия:

a) под каждым участком эпюры лежал линейный (без изломов и скачков) участок эпюры ;

б) можно было применить известные формулы для вычисления площадей _i участков эпюры и положение центров тяжести этих площадей;

в) изгибная жесткость EJ_х на каждом участке была постоянной.

4. Вычисляют площади _i и ординаты эпюры, расположенных под центрами тяжести площадей_i.

5. Применяют формулу Верещагина, суммируя произведения . Эту операцию называют перемножением эпюр и . Действительное направление искомого перемещения определяется так же, как в методе Мора.

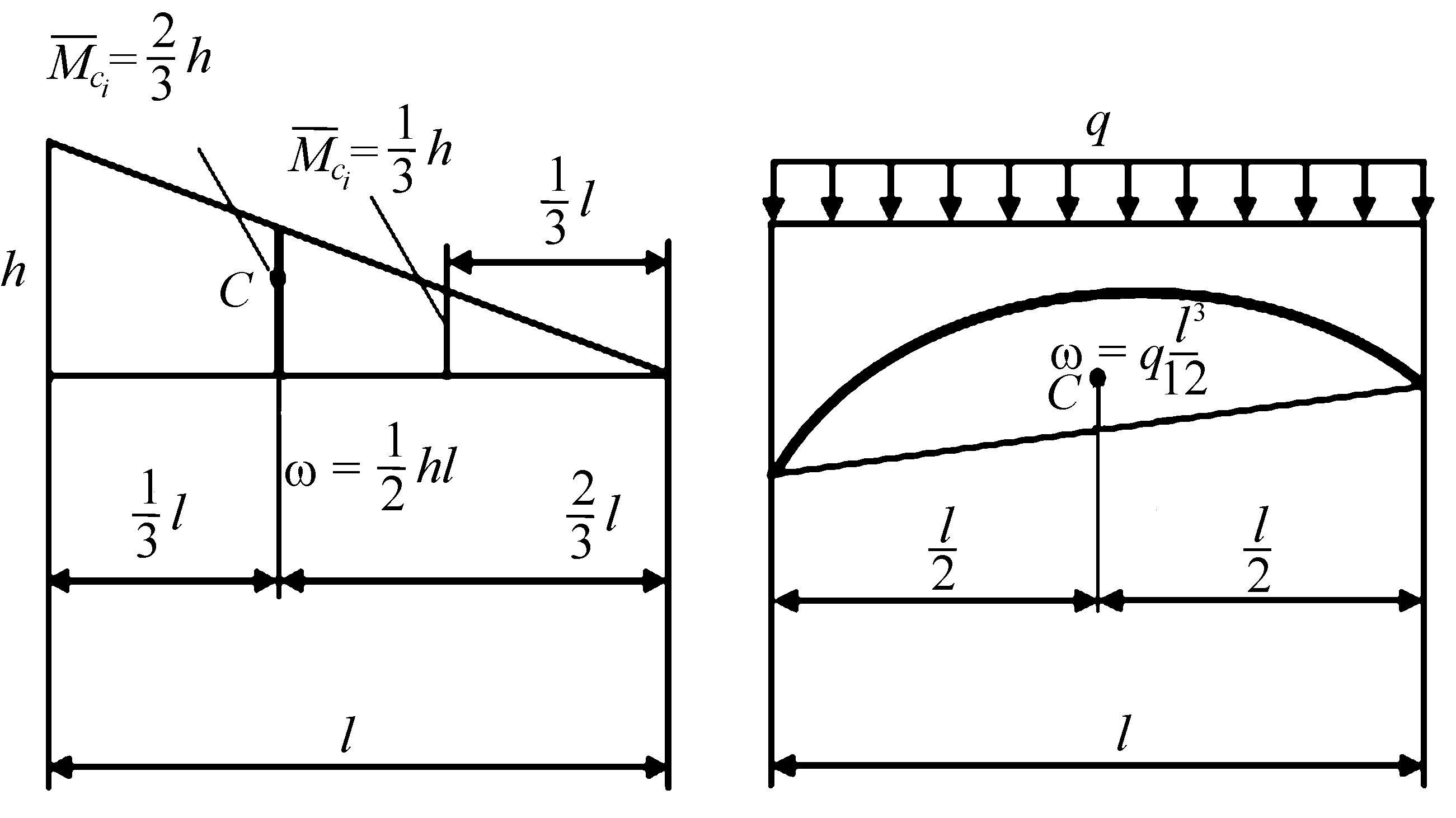
а б

Рис. 7.5

Для того чтобы пользоваться формулой Верещагина, надо знать площадь  и положение центра тяжести для характерных фигур. На рис. 7.5 приводятся необходимые справочные данные.

7.5. Примеры определения перемещений методом Мора и способом Верещагина Пример

Для заданной стальной балки (рис.7.6, а) подобрать стандартный двутавр из условия прочности. Определить прогиб и угол поворота сечения С, [] = 160 МПа, Е = 210⁵ МПа.

Решение

Рис. 7.6

1. Составить уравнения поперечных сил Q_y и изгибающих моментов М_F от внешней нагрузки и построить их эпюры.

Для консольных балок эпюры Q и М можно строить без определения реакций в заделке, если анализ на участках проводить со стороны свободного конца балки в направлении защемления. Выделим балки и участки балки (см. рис. 7.6, а), запишем выражения внутренних усилий и найдем их значения на границах участков.

Строим эпюру Q_y (рис. 7.6, б) и М_F (рис. 7.6, в).

2. Подобрать двутавровое сечение из условия прочности по _max.

Определяем требуемый момент сопротивления изгибу:

.

Подбираем по ГОСТ 8239–72 двутавр № 27а, у которого W_х = 407,0 см³, момент инерции J_х = 5500 см⁴.

3. Определить прогиб сечения С методом Мора.

Составляем схему единичного нагружения, прикладывая к заданной балке безразмерную силу, равную единице в точке С (рис.7.6, г). Разбиваем схему единичного нагружения на такие же участки, что и на схеме грузового нагружения (см. рис. 7.6, а). Записываем для каждого участка выражения изгибающих моментов от единичной нагрузки .

Записываем интегралы Мора на каждом участке и, суммируя результаты, вычисляем прогиб сечения С.