2.6. Интерполяционные полиномы для дискретизованной области

Интерполяционный полином в общей форме имеет вид

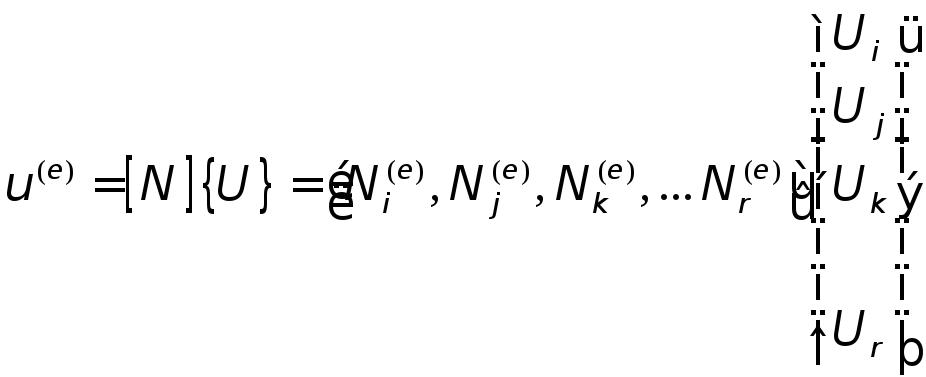. (2.43)

где – число узлов элемента, верхний индексозначает произвольный элемент.

Техника включения элемента в область может быть проиллюстрирована на примере простой пятиэлементной конфигурации, показанной на рис. 2.12 Узлы пронумерованы от единицы до шести. Величины ,,,,,представляют собой глобальные свободы. Координаты узлов,, известны. Номера элементов записаны в круглых скобках.

Для обозначения номеров узлов элемента могут быть использованы принятые выше индексы ,и, как только определен первый узел в каждом элементе. На рис. 2.12-й узел в каждом элементе выделен звездочкой. Выбор этого узла совершенно произволен, хотя читатель вскоре сам убедится в удобстве именно такого расположения первых узлов. Узлы‚ миследуют за-м узлом в направлении против часовой стрелки. Фиксирование узлапозволяет записать следующие равенства для первого элемента:

, ,.

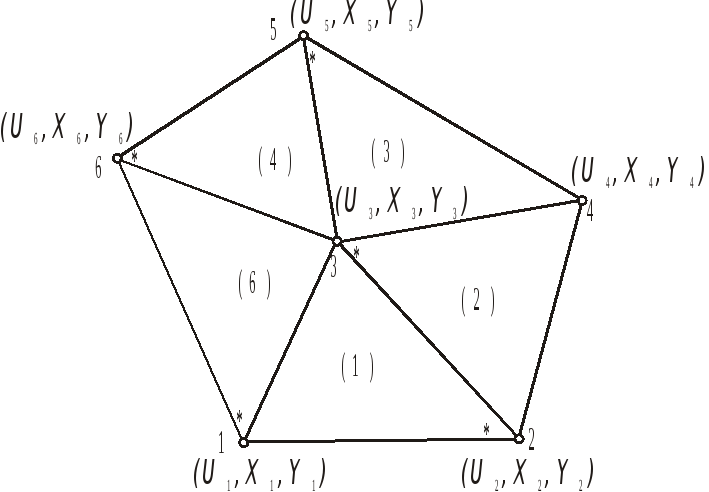
Рис. 2.13. Пятиэлементная область

Соответствие такого же типа может быть установлено для других элементов:

элемент 2: ,,,

элемент 3: ,,,

элемент 4: ,,,

элемент 5: ,,,

С помощью этих соотношений можно осуществить включение элемента в область, так как они ставят в соответствие индексы элемента ,иглобальным номерам узлов. Этот процесс фиксирует координаты узлов элемента.

Значения индексов ,имогут быть подставлены в формулу (2.43), что приводит к следующей совокупности уравнений для элементов

, (2.44)

Функции формы – множители при узловых значениях в формулах (2.44) – определяются подстановкой числовых значений ,ив уравнения для функций формы.

С помощью уравнений (2.44) достигается основная цель. Конечные элементы объединяются в ансамбль, а интерполяционные функции выражаются через глобальные узловые значения и глобальные координаты, которые вводятся вместо произвольных ,и.

Каждое из уравнений в системе (2.44) содержит глобальные узловые значения, но относится к конкретному элементу. Мы будем а дальнейшем использовать расширенную форму этих уравнений, которая имеет вид

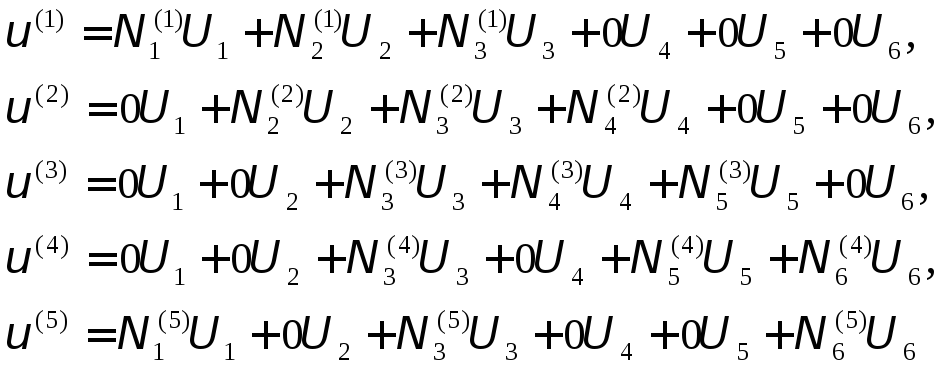, (2.45)

Эти уравнения можно записать следующим образом:

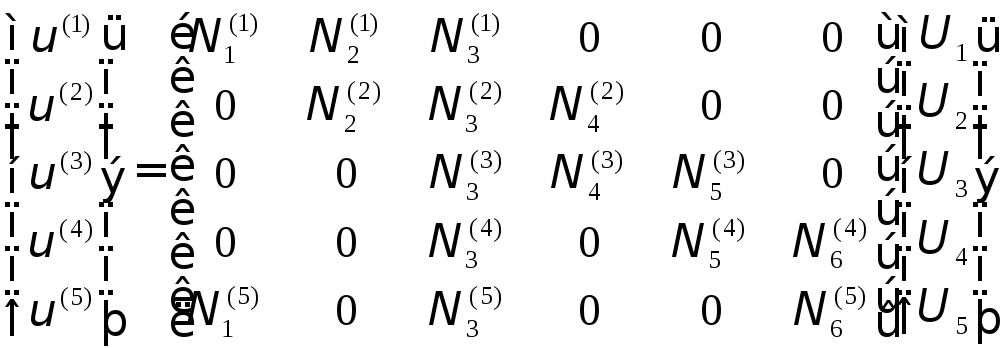. (2.46)

Сокращенная форма интерполяционных уравнений используется, когда осуществляется машинная реализация метода. Расширенная форма имеет некоторое преимущество, когда рассматривается процесс минимизации, который связан с дифференцированием матриц элементов.

2.7. Преобразование системы уравнений

Результирующая система уравнений имеет вид

(2.47)

она получается суммированием уравнений для всех элементов. Эта система должна быть преобразована, если некоторые составляющие {T} известны, что является скорее правилом, чем исключением. В большинстве задач теории поля некоторые граничные значения искомой величины заданы; во всех задачах теории упругости должны быть фиксированы некоторые перемещения, с тем, чтобы исключить перемещение среды как жесткого тела. В задачах механики деформируемых сред матрица жесткости [K] будет сингулярной до тех пор, пока не заданы некоторые перемещения.

Цель этого раздела ­­– обсуждение и иллюстрация процедуры преобразования [K] и {F} таким образом, чтобы получить правильный ответ, не изменяя размеры [K] и {F}, ибо это повлечет за собой трудности при программировании.

Если фиксирована одна степень свободы узлового параметра {T}. То преобразование системы уравнений представляет собой двухшаговую процедуру. Пусть, например, известно значение Т5; преобразование сводится только к следующему:

1. Все коэффициенты пятой строки, за исключением диагональных, приравниваются нулю. Диагональный член остается неизменным. В форме равенства это выглядит как 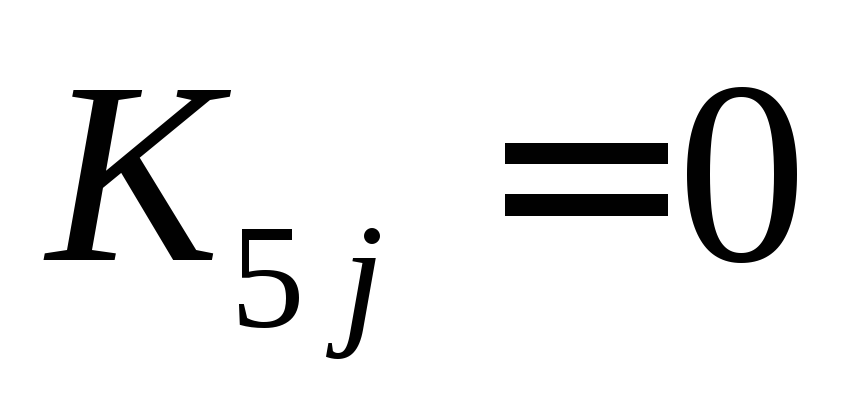при j=1,…,n и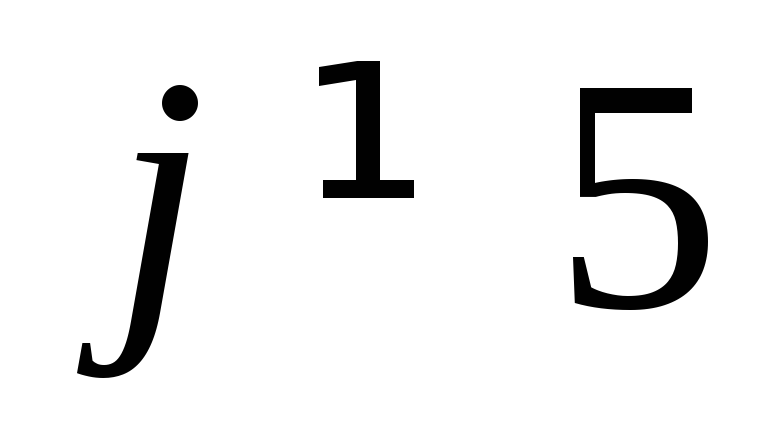. Соответствующая компонента F5 вектора {F} заменяется на произведение:

2. Все остальные уравнения преобразуются вычитанием произведения

из F_jи подстановкойK_j5=0, j=1,…,n, j≠5.

Пример

Требуется преобразовать следующую систему уравнений, если известно, что Т₁=150 иТ₅= 40:

На первом этапе приравняем нулю все коэффициенты в первой и пятой строках, за исключением диагональных членов, которые оставим неизменными. Компоненты F₁ и F₅ в {F} заменим соответственно на K₁₁T₁ и K₅₅T₅. В результате будем иметь:

Второй этап состоит в исключении столбцов матрицы, коэффициенты которых умножаются на Т₁иТ₅. Это осуществляется переносом членов, содержащихТ₁иТ₅в правую часть системы. Например, величинаF₂становится равной 2000+46Т₁, или 8900. Завершая второй шаг, получим:

Описанная выше процедура совершенно проста и легко поддается программированию. Та же методика преобразования может быть использована также в случае, когда [K] хранится в виде прямоугольного массива. Логика программирования, однако, при этом более сложная.

Другой метод, применяемый некоторыми исследователями, состоит в том, что диагональный коэффициент, соответствующий заданному узловому значению Т_β, умножается на очень большое число, скажем на 10¹⁵, аF_βзаменяется на (10¹⁵)Т_β. Это равносильно приближенной замене коэффициентов вне главной диагонали нулям. Такой способ очень легко реализовать на ЭВМ, но он неприменим, если значениеТ_βочень мало. Именно с таким случаем сталкиваются при решении задач механики твердого деформируемого тела, когда заданные перемещения малы по величине. Первый метод, рассмотренный выше, всегда будет давать правильные результаты там, где мы сталкиваемся с малыми заданными величинамиТ_β.