referat - копия

Содержание:

• Введение………………………………………………………….…стр. 2

• Определение фрактала……………………………………….…..стр. 3

• История появление фракталов…………………………………..стр. 4

• Возникновение теории фракталов……………………………....стр. 4 – 5

• Модель Мандельброта…………………………………………....стр. 5 – 7

• Модель Джулии………………………………………………….....стр. 7 – 8

• Ковер Серпинского………………………………………………...стр. 8

• Кривая Коха………………………………………………………...стр. 8 - 9

• Фракталы в природе………………………………………………стр. 10 - 11

• Культура…………………………………………………………….стр. 11 - 12

• Математическая теория фракталов…………………………….стр. 13

• Самоподобие………………………………………………………стр. 14

• Размерность………………………………………………………..стр. 15 -16

• Примеры применения фракталов в архитектуре………...стр. 17 - 22

• Примеры применения фракталов в градостроении……..стр. 23 - 28

• Заключение……………………………………………………..стр. 29

Введение

«До чего дошел прогресс, до невиданных чудес...»- именно такими словами песни из кинофильма «Электроник» можно дать характеристику развитию современной науки, техники и, конечно же, архитектуры.

Новые науки - фрактальная геометрия, теория самоорганизации, нелинейная динамика, неокосмология и др. принесли с собой изменение взглядов на жизнь, мировоззренческой перспективы - от механистического взгляда на вселенную до понимания, что на всех уровнях вселенная находится в процессе самоорганизации.

Актуальность подобных наук (и в частности фрактальной геометрии) в современном мире очевидна, ведь они нашли свое применение в различных сферах деятельности человека: компьютерной графике, компьютерном проектировании зданий и сооружений, аналитике, литературе, естественных науках, архитектуре, медицине.

Думаю, что толчком для развития подобных сложных систем стало стремление к разрешению глобальных проблем человечества, преодоление «духовного кризиса» общества, «кризиса идей» (который, я считаю, проявляется даже в студенческих проектах), а также понимание, что природа обладает сложностью совершенно иного уровня, чем предполагалось ранее. Человек - создание природы и появление новых теорий, новых архитектурных форм (порой даже фантастических) - это следствие эволюции. Давно прошла эпоха великих открытий, «золотых» и «серебряных» веков. Думаю, что последние несколько десятилетий человек лишь усовершенствует уже созданные и придуманные «вещи». А появление «наук о сложных системах» дает нам шанс реабилитироваться, очнуться ото «сна» и начать новый век технологий.

Определение фрактала

Что же означает «странное» слово «фрактал»? Термин «фрактал» (от латинского fractus - «дробный») обозначает изломанную самоподобную структуру, обладающую дробной размерностью. Фракталы - это геометрические объекты с удивительными свойствами: любая часть фрактала содержит его уменьшенное изображение, это множества, описываемые единым законом на всех уровнях организации; геометрическая структура с дробной размерностью, обладает свойством рекурсивности. Под фрактальностью понимается наличие у объекта какого-либо из фрактальных свойств, выраженного в динамическом или статическом состоянии. Фрактальные структуры обладают следующими свойствами: самоподобностью или иерархическим принципом организации; дробной размерностью; способностью к развитию: в простом алгоритме заключен потенциал для развития множества вариаций; принадлежностью одновременно и к хаосу, и к порядку.

Все перечисленные свойства обуславливают широчайшее распространение фрактальных структур, как в естественной, так и в искусственной средах.

История появление фракталов

 Теория фракталов  имеет  совсем   небольшой возраст. Она появилась   в конце шестидесятых годов  на стыке  математики, информатики, лингвистики и биологии.  В то время   компьютеры все больше проникали в жизнь  людей, ученые начинали применять их в своих исследованиях, росло  число пользователей вычислительных машин.  Для массового использования компьютеров необходимо стало  облегчить  процесс общения  человека с машиной. Если в самом начале компьютерной эры  немногочисленные программисты-пользователи самоотверженно   вводили команды в машинных кодах и получали результаты в виде бесконечных лент бумаги,  то при  массовом  и загруженном режиме  использования компьютеров   возникла необходимость в изобретении такого языка программирования, который  был бы понятен для машины, и в то же время, был бы прост в изучении и  применении. То есть  пользователю требовалось бы ввести только одну команду,  а   компьютер  разложил бы ее на более простые, и выполнил бы уже их. Чтобы облегчить  написание трансляторов, на стыке информатики и лингвистики  возникла теория фракталов, позволяющая  строго задавать   взаимоотношения между  алгоритмическими языками. А датский математик  и биолог А. Линденмеер придумал в 1968 году одну такую грамматику, названную им L-системой, которая, как он полагал, моделирует  также рост живых  организмов, в особенности образование кустов и веток у растений.

  Вот как выглядит его модель. Задают алфавит  - произвольный  набор символов. Выделяют одно, начальное слово, называемое аксиомой, - можно считать, что оно соответствует исходному состоянию организма – зародышу. А потом описывают правила замены каждого  символа алфавита  определенным набором символов, то есть задают  закон развития зародыша. Действуют правила так: прочитываем  по порядку  каждый символ  аксиомы и заменяем его на слово, указанное в правиле замены.

      Таким образом, прочитав аксиому  один раз, мы получаем новую строку символов, к которой снова   применяем  ту же процедуру. Шаг за шагом возникает все более  длинная строка –  каждый из таких шагов можно считать одной  из  последовательных стадий развития «организма». Ограничив число шагов, определяют, когда развития считается законченным.

Возникновение теории фракталов

      Отцом фракталов по праву можно считать  Бенуа Мандельброта.  Мандельброт  является  изобретателем    термина «фрактал».  Мандельброт писал: « Я   придумал слово «фрактал», взяв за основу латинское  прилагательное  «fractus», означающее нерегулярный, рекурсивный, фрагментный».  Первое определение фракталам также дал Б. Мандельброт: 

      Фрактал – самоподобная структура, чье изображение не зависит от масштаба. Это рекурсивная модель, каждая часть которой повторяет в своем развитии  развитие всей модели в целом.

На сегодняшний день  существует много различных  математических моделей фракталов.  Отличительная особенность каждой из них является то,

что в их основе лежит   какая-либо рекурсивная функция, например: x_i=f(x_i-1). С  применением ЭВМ у исследователей появилась возможность  получать графические изображения фракталов.  Простейшие модели не требуют больших вычислений и их можно реализовать прямо на уроке информатики,  тогда как  иные модели настолько требовательны к  мощности компьютера, что их реализация  осуществляется с применением суперЭВМ. Кстати,  в  США изучением фрактальных  моделей занимается Национальных Центр Приложений для Суперкомпьютеров (NCSA).  В данной работе мы хотим  показать только несколько моделей фракталов, которые нам удалось получить.

Модель Мандельброта

       Бенуа Мандельброт  предложил модель фрактала, которая уже стала классической и часто  используется для демонстрации   как типичного примера самого фрактала, так  и для демонстрации красоты фракталов, которая также привлекает исследователей, художников, просто  интересующихся людей.

       Математическое описание модели следующее:  на комплексной плоскости в неком интервале для каждой точки с  вычисляется  рекурсивная функция   Z=Z²+c.  Казалось бы, что такого особенного в этой функции? Но  после N повторений данной  процедуры вычисления   координат точек, на комплексной плоскости  появляется удивительно красивая  фигура, чем-то напоминающая грушу.

       В модели Мандельброта  изменяющимся фактором является начальная  точка с, а  параметр z, является зависимым. Поэтому  для построения фрактала Мандельброта существует правило: начальное значение z равно нулю (z=0)!  Это ограничение вводится для того, чтобы первая производная от функции  z  в начальной точке была равна нулю.  А это означает, что в начальной точке  функция имеет минимум, и в дальнейшем она будет принимать  только большие значения.

Мы хотим заметить, что если  рекурсивная  формула фрактала имеет другой вид,   то тогда следует выбирать  другое значение  начальной точки для параметра Z. Например, если формула имеет вид z=z²+z+c,  то начальная точка будет равна: 

2*z+1=0  Ю  z= -1/2. 

Рис.1   Фрактал Мандельброта

       Вам уже известна математическая модель фрактала Мандельброта. Теперь мы   покажем, как  она реализуется графически.  Начальная точка модели  равна нулю. Графически она соответствует центру тела “груши”.  Через N шагов заполнятся все тело груши и в  том месте, где закончилась последняя итерация, начинает образовываться  «голова»  фрактала.   «Голова» фрактала будет  ровно в четыре раза  меньше тела, так как  математическая формула  фрактала представляет из себя квадратный полином.  Затем опять через N  итераций у «тела» начинает образовываться  «почка» (справа и  слева от «тела»).  И так далее. Чем больше задано числе итераций N, тем более детальным получится изображение фрактала, тем больше будет у него  различных отростков.  Схематическое изображение стадий роста фрактала   Мандельброта  представлено на рис.2:

Рис.2   Схема образования фрактала Мандельброта

      Из рисунков 1 и 2 видно, что каждое последующее образование  на «теле»  точно повторяет  в своем строении само тело.  Это и есть отличительная  черта того, что данная модель является фракталом.

       На следующих рисунках  показано, как будет изменяться положение  точки, соответствующей параметру z,   при различном  начальном положении  точки c.

А) Начальная точка в «теле» 

Б) Начальная точка в «голове»

В) Начальная точка в «почке»

Г) Начальная точка в «почке» второго уровня

Д) Начальная точка в «почке» третьего уровня

Из рисунков  А - Д   хорошо видно, как  с каждым шагом все более усложняется структура фрактала  и у параметра  z   все более сложная траектория.

     Ограничения на модель Мандельброта:  существует доказательство, что в модели Мандельброта   |z|<=2   и  |c|<=2. 

Модель Джулии 

      Модель фрактала Джулии  имеет   то же уравнение, что и модель Мандельброта: Z=Z²+c,    только  здесь    переменным параметром является не  c,   a  z.

Соответственно, меняется вся структура фрактала, так как теперь на начальное положение  не накладывается никаких ограничений.   Между  моделями Мандельброта и Джулии существует такое различие: если модель Мандельброта  является статической ( так как z начальное всегда равно нулю), то модель Джулии является динамической моделью    фрактала.   На рис. 3  показано графическое представление фрактала Джулии.

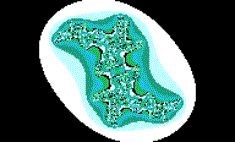
Рис. 3 Модель Джулии

       Как видно из рисунка фрактала, он симметричную относительно центральной точки форму, тогда как  фрактал Мандельброта имеет форму, симметричную относительно  оси.

Ковер Серпинского

       Ковер Серпинского считается еще одной моделью  фрактала. Строится он  следующим образом: берется  квадрат, делится на девять квадратов,    вырезается центральный квадрат.  Затем  с каждым из восьми  оставшихся квадратов проделывается подобная процедура. И так до бесконечности.   В результате вместо  целого квадрата мы получаем ковер со своеобразным симметричным рисунком.  Впервые данную модель предложил математик Серпинский, в честь которого он и получил свое название.   Пример ковра Серпинского можно увидеть на рис. 4.

  

Рис.4 Построение ковра Серпинского

Кривая   Коха

     В начале  ХХ века математики  искали   такие кривые, которые ни в одной точке не имеют  касательной.  Это означало, что кривая резко меняет свое направление, и притом с колоссально   большой скоростью (производная равна бесконечности).  Поиски данных кривых были вызваны не просто праздным интересом математиков. Дело в том, что  в начале ХХ  века очень бурно развивалась   квантовая механика.  Исследователь М.Броун    зарисовал  траекторию движения взвешенных частиц в воде и  объяснил это явление так:  беспорядочно движущиеся атомы жидкости ударяются  о взвешенные частицы и тем самым приводят их в движение.  После такого объяснения броуновского движения перед учеными встала задача найти такую кривую, которая   бы наилучшим образом аппроксимировала  движение броуновских частиц.   Для  этого кривая должна была отвечать следующим свойствам:  не иметь касательной  ни в одной точке.  Математик Кох предложил  одну такую кривую. Мы не будем вдаваться в  объяснения правила ее построения, а просто приведем ее изображение, из которого все станет ясно (рис.5).

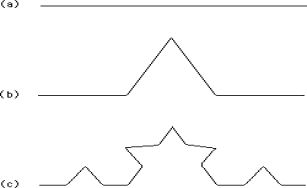
Рис.5  Этапы построения кривой Коха

       Кривая Коха является еще одним примером фрактала, так как   каждая ее часть является уменьшенным изображением всей кривой.

         6.  Графические изображения различных фракталов

Рис. 6  Примеры  графического представления фракталов

Фракталы в природе 

Множество процессов, происходящих в природе и обществе – от космических до социальных и физиологических, – характеризуется хаотической фрактальной динамикой. Фрактальность природных объектов подтверждается возможностью построения весьма правдоподобных компьютерных ландшафтов виртуального мира на основе простых фрактальных программ, в которых приближение к реальности достигается некоторой степенью нерегулярности путем введения случайных чисел. Морфогенез растений также успешно имитируется подобными программами. Моделирование морфогенеза животных на всех уровнях их организации – динамично развивающаяся область биологии. Биологические структуры сложной пространственной организации могут быть количественно охарактеризованы путем определения фрактальной размерности, служащей показателем морфологической сложности этих структур. Вовлечением фрактальных алгоритмов в биологический морфогенез обеспечивается сжатое генетическое кодирование. Фракталоподобные структуры живой природы характеризуются ограниченной шкалой повторов и менее хаотизированы по сравнению с фракталами неживой природы; как правило, это мультифракталы, т.е. неоднородные фракталы.

Культура

Использование подходов фрактальной геометрии позволяет выявить сходство ряда живых и неживых объектов – как природных, так и созданных человеком. Один из примеров такого параллелизма формообразования дает сопоставление конструкций геодезических куполов с организацией молекул фуллеренов, макромолекулярных комплексов клеток многоклеточных животных и скелетных структур радиолярий. Строительные конструкции геодезических куполов были запатентованы в 1954 г. Р.Б.Фуллером (1895–1983), американским изобретателем, архитектором и философом; в нашей стране такими разработками занимался М.С.Туполев. Геодезические купола могут быть образованы сложной сетью треугольников, которые формируют поверхность, близкую к сферической. Повторные подразделения на треугольники, характерные для геодезических куполов, образуют фрактальный алгоритм. Конструкции с таким триангуляционным разбиением оказались не только перспективными в архитектуре, но и очень сходными с природными формами.

В 90-е годы прошлого века было получено новое вещество – фуллерит, состоящее из молекул углерода, фуллеренов (этимология названий фуллеренов и фуллерита весьма прозрачно связана с именем Фуллера). Фуллериталлотропная модификация углерода, третья кристаллическая форма углерода (две ранее известные формы – графит и алмаз). Молекулы фуллеренов представляют собой замкнутую поверхность в форме сферы или сфероида, на которой располагаются атомы углерода. Конструкции геодезических куполов подобны и некоторым биологическим структурам, например макромолекулярным комплексам клатрина, сети пучков актиновых филаментов клеток многоклеточных животных и скелетам некоторых радиолярий, одноклеточных организмов.

Математическая теория фракталов

Как построить математическую модель таких объектов с определенной степенью подробности описания их геометрической формы?

Вообще, всякая математическая модель есть некоторая абстракция, отражающая выбранные существенные свойства рассматриваемых реальных объектов, процессов (физических ситуаций). В результате процедуры выделения и формализации (выражения содержания изучаемого явления через знаковые формы – символы, знаки, термины, буквенные обозначения и др.) получают математическое описание явления, т. е. его математическую модель, которую далее можно исследовать математическими методами как математическую задачу, математическую проблему. Формализация позволяет производить логические умозаключения (выводы), вычислительные операции, исследования структуры, обращаясь непосредственно со знаковыми формами (с формулами, геометрическими построениями, логическими суждениями), абстрагируясь от конкретного содержания явления.

Использование математических моделей (и результатов исследований этих моделей) происходит на основе их интерпретации в реальных ситуациях. При этом использование будет оправданным (правомерным) и эффективным, если модель будет достаточно адекватной, а полученные математические результаты практически реализуемы. Для понимания некоторого данного явления (на основе его математического описания) математика вырабатывает, подобно обычному языку, метафоры (образные представления), позволяющие объяснить это явление, ставя ему в соответствие другое явление, более привычное или воспринимаемое как таковое.

Фракталы представляют собой математические модели сложных структур, пространственное изображение которых представляется в виде сломанных, морщинистых и нечетких форм. Фракталы (как математические абстракции) обладают следующими характерными свойствами, отображающими их иррегулярную сущность:

• самоподобие (иерархический принцип организации);

• способность к развитию (принцип непрерывности формообразования);

• дробная метрическая размерность (принцип сингулярности меры);

• размытость, нечеткость контуров (принцип неопределенности границ);

• геометрическое представление хаотической динамики (принцип динамического хаоса).

Фрактальные структуры (с перечисленными характерными свойствами) имеют широкое распространение, как в естественной, так и в искусственной средах.

Самоподобие

Самоподобие в математических алгоритмах реализуется с помощью рекурсивных процедур. Вообще, рекурсия – способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Преимущество рекурсивного определения объекта (действия) заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов (действий, итераций), бесконечную итерационную процедуру (вычислений, построений) действий. Практически все геометрические фракталы задаются в форме бесконечной рекурсии.

Пространственная форма фрактала повторяется (повторяет себя) в каждом фрагменте в любом масштабе. Его структура отражает иерархический принцип организации материи в природе. При увеличении масштаба видимая структура не упрощается, на всех шкалах проявляется одинаково сложная картина.

Способность фрактальных структур к развитию определяет непрерывность процесса формообразования, незавершенность пространственного представления фрактала на каждом текущем шаге итерационного процесса построения. Фрактал никогда не бывает законченным.

Фрактал есть итоговый результат бесконечной процедуры, т. е. является бесконечным в развитии. Нельзя изобразить бесконечность процесса, нельзя реально выполнить бесконечную рекурсивную процедуру. Это можно только мыслить. Поэтому всякое наглядное представление фрактала – это на самом деле изображение квазифрактала (некоторого приближения искомого фрактала), определяется конечной процедурой (процесс построения останавливается на каком-то конечном шаге). При некотором большом масштабе его фрактальная структура исчезает (т. е. отсутствует повторение базовой формы в уменьшенном виде, начиная с некоторого уровня, определяющего степень уменьшения).

Размерность

Математическое понимание фрактала определяет его как множество с дробной размерностью. Дробное значение фрактальной размерности характеризует степень заполнения пространства фрактальной структурой, тогда как значение лакунарности представляет собой меру неоднородности структуры фрактала. Количественная характеристика структур сложной пространственной организации через фрактальную размерность может служить показателем морфологической сложности этих структур. Таким образом, определяется природный морфогенез (сложная пространственная организация природных (естественных) форм) в сопоставлении с фрактальными структурами. Следует заметить, что архитектурные формы более регулярны, чем природные, включают меньшее число повторов с их вариациями.

Выясним теперь, какой физический смысл имеют обобщенные фрактальные размерности d_q для некоторых конкретных значений q. Так, при q=0 из выражения