
- •Содержание
- •Сила давления жидкости на криволинейные поверхности
- •Построение тела давления
- •Построение эпюр избыточного гидростатического давления жидкости
- •Гидродинамика уравнение бернули без учета потерь напора (энергии)
- •Уравнение бернулли с учетом потерь напора (энергии)
- •Построение линий полного и пьезометрического напоров для реальной жидкости
- •Гидродинамика. Теоретическая часть
Содержание
Гидростатика
Задачи
Давление в покоящейся жидкости
Сила давления жидкости на криволинейные поверхности
Схемы
Построение тел давления
Построение эпюр избыточного гидростатического давления жидкости
Вопросы
Вопрос 1
Вопрос 2
Гидродинамика
Задачи
Уравнение Бернулли без учета потерь напора (энергии)
Уравнение Бернулли с учетом потерь напора (энергии)
Схемы
Построение линий полного и пьезометрического напоров для реальной жидкости
Вопросы
Вопрос 1
Вопрос 2
Список литературы
 ГИДРОСТАТИКА
ДАВЛЕНИЕ
В ПОКОЯЩЕЙСЯ ЖИДКОСТИ
ГИДРОСТАТИКА
ДАВЛЕНИЕ
В ПОКОЯЩЕЙСЯ ЖИДКОСТИ
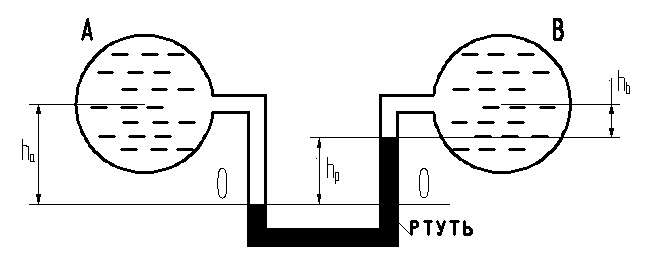
Задача 2-57. Определить разность давлений в резервуарах А и В, заполненных бензином, если показание дифференциального ртутного манометра hp задано.
|
Дано: hp = 80 мм |
СИ 0.08 м |
 P
-
? Па
P
-
? ПаРешение:
Составим уравнение равновесия системы относительно плоскости сравнения 0-0, взятой по нижней линии раздела между бензином и ртутью:
![]()
далее, группируем давления в правой части уравнения, а слева высоты столбов бензина и ртути:
![]()
учитывая, что ha - hb = hp уравнение примет вид:
![]()
подставим значения показания манометра, плотности бензина =730 кг/м3, ртути =13547 кг/м3 [плотности бензина и ртути взяты из таблицы П-3]1
![]()
Выполним проверку размерности:
![]()
Ответ: P = 10058.8 Па
Сила давления жидкости на криволинейные поверхности
 Задача
2-190.
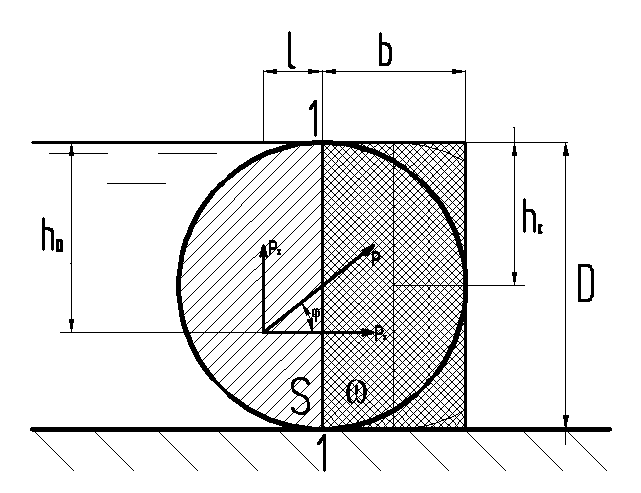
Определить величину и направление силы
гидростатического давления воды на 1
метр ширины вальцового затвора диаметром
D.
Задача
2-190.
Определить величину и направление силы
гидростатического давления воды на 1
метр ширины вальцового затвора диаметром
D.
|
Дано: D = 2 м b = 1 м |
СИ 2 м 1 м |
 ешение:
ешение:
P - ? - ?
Стенка вальцового затвора представляет собой цилиндрическую криволинейную поверхность, простирающаяся перпендикулярно плоскости чертежа на ширину b.
Сила
гидростатического давления P
(ро) на криволинейную поверхность
равна:
![]() Для
нахождения искомой величины полного
давления найдем горизонтальную
составляющую силы давления на затвор.
Как
известно, горизонтальная составляющая
Px
не зависит от формы смоченной криволинейной
поверхности и определяется как силовое
воздействие жидкости на её вертикальную
проекцию.
Для
нахождения искомой величины полного
давления найдем горизонтальную
составляющую силы давления на затвор.
Как
известно, горизонтальная составляющая
Px
не зависит от формы смоченной криволинейной
поверхности и определяется как силовое
воздействие жидкости на её вертикальную
проекцию.
![]() где
hc
величина
заглубления центра тяжести вертикальной
проекции под уровень свободной поверхности
жидкости.
-
площадь
вертикальной
проекции криволинейной поверхности.
где
hc
величина
заглубления центра тяжести вертикальной
проекции под уровень свободной поверхности
жидкости.
-
площадь
вертикальной
проекции криволинейной поверхности.
Так как, не заданы условия, влияющие на плотность воды, то для удобства вычислений возьмем плотность равную =1000 кг/м3, а ускорение свободного падения g=9.81 м/с2
![]()
![]() подставим все величины в формулу и
получим:
подставим все величины в формулу и
получим:
![]()
 Вертикальная
составляющая Pz
равна
весу воды в объеме тела давления, которое
в данном случае представляет собой
полуцилиндр.
Вертикальная
составляющая Pz
равна
весу воды в объеме тела давления, которое
в данном случае представляет собой
полуцилиндр.
![]() ,
где W
объем
полуцилиндра высотой равной b,
а S
площадь круга равная
,
где W
объем
полуцилиндра высотой равной b,
а S
площадь круга равная ![]() , подставив данные уравнение примет
вид:
, подставив данные уравнение примет
вид:
![]()
Тогда суммарная сила давления P будет равна
![]()
Далее,
найдем точку приложения сил, т.е. найдем
ее координаты. Составляющая Px
проходит на расстоянии hD
от свободной поверхности жидкости, и
есть ни что иное как заглубление центра
давления вертикальной проекции боковой
поверхности затвора. Проекция представляет
собой прямоугольник со сторонами равными
b
и D.
Отсюда
следует:
![]() подставив, D
= 2 м получим:
подставив, D
= 2 м получим:![]()
Вертикальная
составляющая Pz
проходит на расстоянии l
от линии 1-1, для его вычисления воспользуемся
готовой формулой, ![]() где r
это
радиус затвора. Итак, подставив численные
значения, имеем:
где r
это
радиус затвора. Итак, подставив численные
значения, имеем:
![]()
Равнодействующая сила P приложена под углом к горизонту и проходит через центр круга, причем:
![]()
Проверка размерности конечной величины P сводится к проверке величин ее составляющих:
![]()
Ответ: P = 24 943, 07 Н, = 38o 10’
