20. Двойной интеграл.Определение.Случай прямоугольной площади.Свойства,сведение к повторному.

Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных  z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как

где R - область интегрирования в плоскости Oxy. Если определенный интеграл от функции одной переменной выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).

Рис.2

Рис. 1

Формально двойной интеграл можно ввести как предел суммы Римана. Пусть, для простоты, область интегрирования R представляет собой прямоугольник (рис2). Используя ряд чисел{ x₀, x₁, ..., x_m }, разобьем отрезок [a, b] на малые интервалы таким образом, чтобы выполнялось соотношение

Аналогично, пусть множество чисел является разбиением отрезка [c, d] вдоль оси Oy, при котором справедливы неравенства

Суммой Римана функции f (x,y) над разбиением называется выражение

где - некоторая точка в прямоугольнике и .  Двойной интеграл от функции f (x,y) в прямоугольной области определяется как предел суммы Римана, при котором максимальные значения Δx_i и Δy_j стремятся к нулю:

 Следующая теорема дает нам такой способ. Она сводит вычисление двойного интеграла к нахождению однократных интегралов.

Теорема 1. Если функция f(x, y) интегрируема в прямоугольнике P = [a, b] ´ [c, d] и если "x Î [a, b] существует интеграл тогда существует повторный интеграли он равен двойному:

Замечание 1. Если f(x, y) интегрируема на E и "y Î [c, d] существует  то он интегрируем по y на [c, d] и

Свойства двойного интеграла

1.

2.

3., гдеk - константа;

4.Если вобластиR,то  5.Еслив областиR и , то;

6.Если наR и области R и S являются непересекающимися , то .  Здесьозначает объединение этих двух областей.

21.Двойной интеграл.Случай произвольной области.Сведение к повторному.

     Теорема . Пусть выполнены следующие условия: 1) область D ограничена, замкнута и такова, что любая прямая, параллельная оси Oy, пересекает границу этой области не более чем в двух точках, ординаты которых суть y₁(x) и y₂(x), где y₁(x) ≤ y₂(x) (см. Рис. 1); 2) функция f(x, y) допускает существование двойного интеграла

и существование для любого x однократного интеграла

     При этих условиях существует повторный интеграл

(x₁ и x₂ - наименьшая и наибольшая абсциссы точек области D) и справедливо равенство

     (19)

     Доказательство. Обозначим через R прямоугольник со сторонами, параллельными координатным осям, содержащий область D, а через F(x, y) - функцию, совпадающую с f(x, y) в точках области D и равную нулю в остальных точках R. Для функции F(x, y) в прямоугольнике R выполнены все условия теоремы 7, и, стало быть, справедлива формула (13), которая (с учетом того, что F(x, y) равна нулю вне D и совпадает с f(x, y) вD) переходит в формулу (19). Теорема доказана.

22.Вычисление объёма с помощью двойного интеграла.

V=∫((Zверх(х,у)-Zнижн(х,у))dxdy

Пример:

Найти объем тела,ограниченного плоскости х=1,у=х,у=3х,z=0 и поверхностью (парабол).

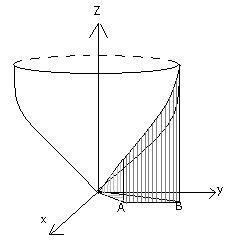Z=0,т.е. плоскость ХОУ-это нижняя поверхность ,т.е. параболоид вращения-это верхняя поверхность.

Опишем область S 0<х<1

у=х –нижняя граница

у=3х- верхняя граница

х<у<3х

V=+