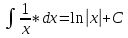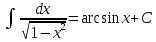матан 2 семестр
Неопределенный интеграл. Первообразная. Определения и свойства.
Опр.1 Функция F(x) наз. первообразной функцией для функций f(x) на некотором промежутке, если F’(x)=f(x) для любого x из этого промежутка.
Например.
f(x)=4x3
; F(x)=x4
Т. к. (x4)’=4x3 , но (x4+1)’=4x3
(x4+2)’=4x3 x4, x4+1, x4+2 - тоже первообразные для 4x3
Теорема.
Если F(x) явл. первообразной для f(x), тогда множество всех первообразных задаётся формулой
F(x)+C, C э R
Док-во:
(F(x)+C)’=F’(x)=f(x)
Докажем, что любая первообразная для f(x) представлена в виде F(x)+C, C э R. Пусть Ф(x) – некоторая первообразная для f(x), т. е. Ф’(x)=f(x)
Тогда рассм. вспомогательную ф-ю ϕ(x)=Ф(x)-F(x) и покажем, что она явл. постоянной.
Пусть x1 и x2 – точки промежутка, пусть x1 < x2
По теореме Лагранжа существует точка ξ(кси) ϵ (x1, x2)
ϕ(x1)- ϕ(x2)= ϕ’(ξ)*( x1- x2)
ϕ’(x)=Ф’(x)-F’(x)=f(x)-f(x)=0
ϕ’(ξ)=0
ϕ(x1)=
ϕ(x2)
ϕ(x)
- постоянная
ч.т.д.
Опр.2
Совокупность всех первообразных ф-й
для f(x)
наз. неопределённым интегралом от ф-ии
f(x)
и обозначается
Например.
Справедливы следующие свойства:
;
a
ϵ R
Таблица интегралов.
Методы интегрирования – подведение под диф-л; замена переменной.
подведение под диф-л
Если
иU=
ϕ(x)
, то
Пример.
;
2) замена переменной
;
упростим, сделав замену x=
ϕ(t),
тогда f(x)=f(ϕ(t))
dx=d ϕ(t)= ϕ’(t)dt
Пример.
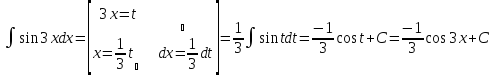
Метод интегрирования по частям
Т.
к.
(U*V)’=U’*V+U*V’
d(UV)=VdU+Udv
UdV=d(UV)-VdU
Пример.
Интегралы от рациональных ф-й
Для
интегрирования рациональной функции
, где P(x) и Q(x) - полиномы, используется
следующая последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
Шаг 1. Преобразование неправильной рациональной дроби
Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочлен P(x) на Q(x). Получим следующее выражение:
Где
- правильная рациональная дробь.
Шаг 2. Разложение знаменателя на простейшие дроби
Запишем многочлен знаменателя Q(x) в виде
где квадратичные функции являются несократимыми, то есть не имеющими действительных корней.
Шаг 3. Разложение рациональной дроби на сумму простейших дробей.
Запишем рациональную функцию в следующем виде:
Общее
число неопределенных коэффициентов
, ... должно быть равно степени знаменателяQ(x).
Затем
умножим обе части полученного уравнения
на знаменатель Q(x)
и приравняем коэффициенты при слагаемых
с одинаковыми степенями x.
В результате мы получим систему линейных
уравнений относительно неизвестных
коэффициентов
, .... Данная система всегда имеет
единственное решение. Описанный алгоритм
представляет собойметод
неопределенных коэффициентов.
Шаг 4. Интегрирование простейших рациональных дробей.
Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где
Пример.
Вычислить
интеграл
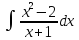
Решение.
Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель.
Получаем
Интегралы от иррациональных ф-й
Для
интегрирования иррациональной функции,
содержащей
используется подстановка
.
Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степеней x,
применяется подстановка в форме
,
гдеn
полагается равным наименьшему общему
кратному знаменателей всех дробных
степеней, входящих в данную функцию.
Рациональная
функция x
под знаком корня n-ой
степени, т.е. выражение вида
,
интегрируется с помощью подстановки
Пример.
Найти
интеграл
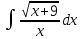
Решение.
Сделаем подстановку:
Интегралы от тригонометрических ф-ий
При нахождении интегралов от тригонометрических функций используется ряд методов:
Использование тригонометрических формул
Понижение степени подынтегральной функции
Метод замены переменной
Универсальная тригонометрическая подстановка
Пример.
Найти неопределенный интеграл.
Используем тригонометрическую формулу
Подводим функцию под знак дифференциала.
Используем табличный интеграл
вопрорс8
площадь криволинейной трапеции
плоская фигура AabB называется криволинейной трапецией f(x)на [a;b] неотриц.непрыравная.
SAabB=?
разобъем отрезок ab точками xi=a+
i=0,1,2....nна отрезки [a,x1],[x1,x2]....[Xn-1,b]. Трапеция разбита на n-полоски. обозначим через mi и Mi -наименьшее и наибольшее значение функции на [Xi-1;Xi]
Очевидно что площадь полоски не меньше чем mi*(Xi-Xi-1) и не больше чем Mi*(Xi-Xi-1) =площадь трапеции не меньше m1
и не больше суммы M1
sn
Если n
Определение- Пусть f(x), x
неотриц.непрерывная,
тогда если предел последовательности
{sn}к
{Sn}существуют
и равны между собой ,то их значения
называются площадью трапеции.Замечание:на каждом отрезке [Xi-1;Xi] выберем произвольную точку C ;Xi-1
;
справедливоmi
Умножим на
и просуммируем =Sn
(2) где f(Ci)*
(3) нпзывается интегральной суммой
функцииf(x)
на [a;b);переходим
в (2) к пределу при n
Независимо от выбора Сi и не обязательно делит [a,b] на равные части ,лишь бы наибольшая часть=0
Физическая задача
Материальная точка движется по прямой преодолевая силу F
положение точки характеризуется координатой x тогда работа A=F*
где
.
Пустьf(x)-переменная
сила, начальная точка x=a,
конечная точка x=bОтрезок [a,b] разбиваем на n точек и частей с одинаковой длиной xi=a+
на каждом участке работа =f*
точность увеличивается при увеличении n, переходим к пределу
A=
Вопрос 9 Определение:]f(X) где X принадлежит [a;b]. Если *.И не зависит от выбора (.)с, то функцияF(X)назыв. Интегрируемой на [a,b], а назыв. Определенным интегралом отf(X) на [a,b] и обозначают.
Вопрос 10 Основныесв-ва определенного интеграла:
Для
.
Док-во-
для
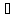интегральной суммыf(x)
=
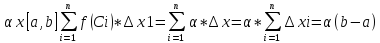
] f(x) инетгрируемв на [a,b] то для
Док-во:
] функции f(x) bg(x) интегрируемы на [a,b] тогда
=
Док-во: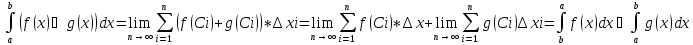
] функции f(x) bg(x) интегрируемы и f(x)
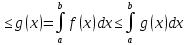
Док-во:f(x)
,
переходя к пределу получаем требуемое.
] f(x) интегрируема на [a,b] = она интегрируема на любом отрезке,содержащемся на [a,b].
Если f(x) интегрируема на [a,c] и интегрируема на [c,b]=она интегрируема и на [a,b].
] на [a,b] справедливо неравенство m
Вопрос 11 Теорема о среднем
Пусть
фу-цияf(x)
непрерывна на [a,b]
тогда на [a,b]сущ-вует
(.)С, что
Док-во:Если
a=b
Если a<b,обозначим m-наименьш.значениеf(x);M-наибольшее значf(x) на [a,b]
Тогда
m
т.кf(x)
непрерывна=принимает любые значения
из [m,M]=пусть(.)С
Если
a>bтогда
,
с
.
Вопрос 12 Определенный интеграл с переменным верхнем пределом.
f(x)
непрерывна на [a,b]=интегрируема
на [a,b]
где x
Рассмотрим
фу-циюF(x)=
Теорема:еслиf(x)-напрерывна
на [a,b]
тогда F(x)
имеет производную на [a,b]
и
(x)=f(x),то
есть
Док-во:из
задания функции F(z)
и 5го св-ва интегралов=F(x)-F(
)=
)=f(
c)
*(x-
)
где с
Если
<X
или С
],
если
>X
Таким
образом для
найдется такое С междуXи
,
что
=f(c)
Так
как f(x)
непрерывна на [a,b]=f(x)
непрерывна и в (.)Cи
в (.)
=
(
)=
)/
x-
=
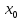=f(
)
В
(.)
=a
,будет правая производная
В
(.)
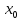=bбудет
левая производная чтд.
Из теоремы следует , что любая напрерывная фу-ция имеет первообразную,которой является определенный интеграл с переменным верхним пределом от данной функции.
Вопрос 13 Формула Ньютона-Лейница
Теорема:
Если функция f(x)
непрерывна на отрезке [a,b]
а функцияF(x)является
первообразной для f(x)
на [a,b]
тогда справедлива формула
/
=F(b)-F(a)
Док-во:По
теореме о диф-нии интеграла по верхнему
пределу функции F(x)=
Это первообразная для f(x)на [a,b].
Т.кF(x)является первообразной для f(x) на [a,b]=Ф(x)-F(x)=С
=Ф(x)=F(x)+C
]x=a=Ф(а)=F(a)+C
]x=b=Ф(b)=F(b)+C
Т.кФ(a)=0
иФ(b)=
=Ф(b)=F(b)-F(a) чтд
Вопрос 14 Метод вычисления опр.Интеграла.Метод замены переменной.
]
функция f(x)
непрерывна в
Тогда
если y(t)
имеет непрырывнуюпроизводную,то
(t)dt1
Док-во:
По условию f(x)
непрерывна=имеет первообразную. Обозначим
ее через F(x)
тогда=сложная функция F(y(t))
будет первообразной для функции
f(y(t))*
(t)
Вычислим
интеграл от функции f(x)
иf(y(t))*
(t)по
формуле Ньютона-лейница=
1чтд.
15.Метод интегрирования по частям
Если функции у=и(х) и v=v(x) имеют непрерывные производные на отрезке [a;b]то имеет место формула
Эта формула называется формулой интегрирования по частям.
В качестве «и» надо брать функцию, которая при дифференцировании упростится.
В качестве «dv» надо брать выражение которое легко интерируется.
Доказательство формулы интегрирования по частям:
На отрезке [a;b]
Имеет
место равенство
,следовательно,
функцияuv
есть первообразная для непрерывной
функции
.Тогда
по формуле Лейбница-Ньютона имеем:
Следовательно,
=>
=>
=>
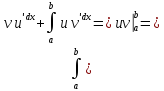
Теорема доказана.