2.3. Расчет тонкостенной трубы,

Подверженной действию внутреннего давления, продольной силы и крутящего момента

(Задача № 9)

Основные формулы

Рис. 2.21. Тонкостенная труба под действием внутреннего

давления, продольной силы и крутящего момента

Рассматривается длинная прямолинейная цилиндрическая тонкостенная труба (рис. 2.21) с,. Труба нагружена внутренним давлением, по ее торцам приложены силыи крутящие моменты.

Напряжения в трубе обозначаем, используя местную декартову систему координат x,y,z: осьxпараллельна оси трубы, осьzнаправлена по касательной к срединной линии поперечного сечения, осьюyслужит продолжение радиусаR.

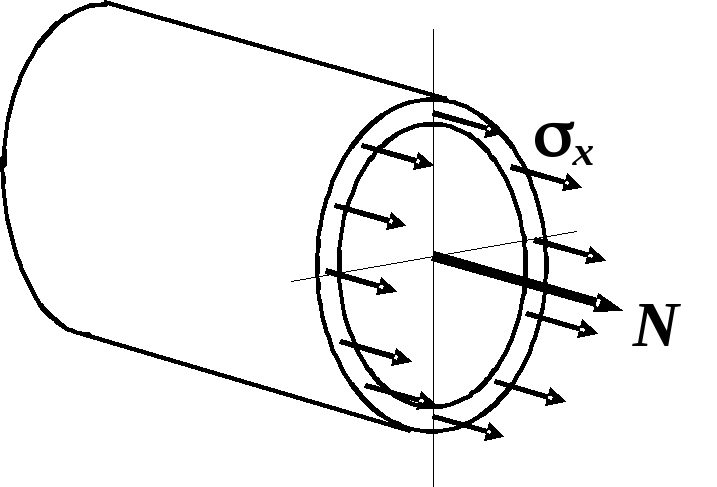
Сила вызывает в поперечном сечении трубы продольное усилиеи создает нормальное напряжение (рис. 2.22)

.

Рис. 2.22. Напряжения

в трубе от продольной силы

Рис. 2.23. Напряжения в трубе от

внутреннего давления

Здесь– площадь поперечного сечения тонкостенной трубы.

Внутреннее давление вызывает растяжение трубы в кольцевом направлении (рис. 2.23), чему соответствует напряжение в продольных сечениях трубы:

.

Рис. 2.24. Напряжения

в трубе от крутящего

момента

Напряженияположительны при. Случайотвечает давлению, приложенному к наружной поверхности.

Крутящий момент создает касательные напряжения (рис. 2.24):

.

Они направлены так, чтобы уравновесить пару сил М.

По толщине трубы напряжения распределены равномерно. Остальные напряжения либо в точности равны нулю, либо малы:,.

Напряженное состояние элементарного параллелепипеда, вырезанного из трубы (рис. 2.25), является плоским. Анализ напряженного состояния выполняется так же, как в задаче № 7.

Условие задачи

Рис. 2.25. Напряженное

состояние точки трубы

Труба с радиусом сечениям толщинойсм загружена продольной растягивающей силойкН, внутренним давлениемМПа и крутящим моментом. Материал трубы – чугун с такими характеристиками:МПа,МПа,. Нормативный коэффициент запаса прочности.

Требуется:

1. найти напряжения на гранях элемента, выделенного из трубы;

2. найти главные напряжения и положения главных площадок;

3. проверить прочность и определить действительный коэффициент запаса прочности;

4. показать направление трещины, возникающей при повышении уровня напряженного состояния до критического.

В расчетно-графической работе студенту требуется, кроме того, вычислить напряжения по указанной наклонной площадке. Это задание выполняется так же, как в задаче № 7.

Решение

Начать решение задачи нужно с изображения трубы и действующих на нее сил. Рядом со стрелками указываются абсолютные значения сил. Знаки учитываются соответствующим направлением стрелок.

Проверим применимость к данной задаче формул для вычисления напряжений в тонкостенной трубе. Так как , то труба является тонкостенной. Следовательно, вышеприведенные формулы применимы.

Нормальное напряжение от продольного растяжения силой

положительно.

Нормальное напряжение, вызванное внутренним давлением ,

МПа

также положительно.

Касательное напряжение, вызванное моментом , по модулю равно

.

Принимая во внимание направление крутящего момента (см. рис. 2.24) и учитывая правило знаков для касательного напряжения при плоском напряженном состоянии, получаем .

Теперь изобразим найденное напряженное состояние точки трубы в виде плоского рисунка, учтя правила знаков для напряжений. Для последующей проверки прочности вычислим главные напряжения:

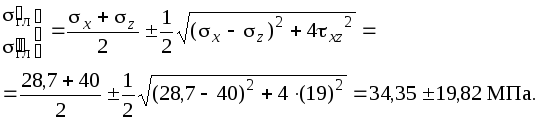
Главные напряжения, пронумерованные должным образом,

,,.

Тангенс угла наклона главной площадки

.

Отсюда два главных угла

.

Соответствие угла главным площадкам (1 или 2) устанавливается так же, как в задаче № 7. Главные направления 1 и 2 показаны на рис. 2.26. Проверку вычисленных значений главных напряжений и главных направлений можно выполнить графически, построив круг напряжений Мора. Построение круга напряжений описано при решении задачи № 7.

Материал является хрупким (чугун), поэтому с целью проверки прочности используем вторую теорию прочности или теорию прочности Мора.

Согласно второй теории прочности

,

значит, прочность обеспечена.

Вычислим действительный коэффициент запаса прочности:

Рис. 2.26. Вероятное

направление трещин

.

Вероятная плоскость отрыва (трещины) перпендикулярна первому главному направлению, то есть наклонена к продольной оси трубы под углом . Она показана на рис. 2.26, где ось– продольная ось трубы. Направление вероятной плоскости отрыва на рисунке привязано к оси конструкции, значит, может быть показано и на самой конструкции.

Согласно пятой теории прочности (теории Мора)

,

то есть прочность также обеспечена. Вычислим фактический коэффициент запаса прочности:

.