
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Индивидуальное домашнее задание №2
по линейной алгебре.
Количество баллов за задачи (суммарно 44 балла):
1. 4 балла
2. 4 балла
3. а), б) 3 балла за каждый пункт
4. 6 баллов
5. 6 баллов
6. 7 баллов
7. 5 баллов
8. 6 баллов
Вариант 1
-
Вычислить определитель:
 .
. -
По формулам Крамера решить систему уравнений :
 .
. -
Найти произведение матриц : а)
 б)
б)
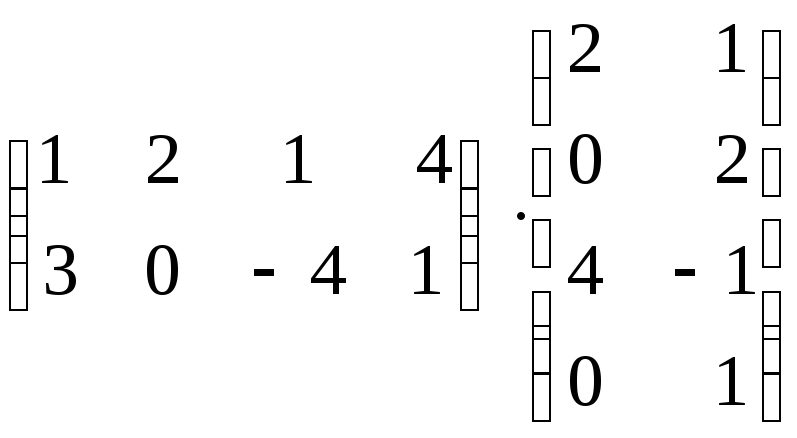
-
Методом Гаусса решить две системы уравнений с одной и той же матрицей :
 ,
,
 .
. -
Методом Гаусса решить систему и представить её решение в базисной форме :
 .
. -
Методом Гаусса решить однородную систему и представить её решение в базисной форме :
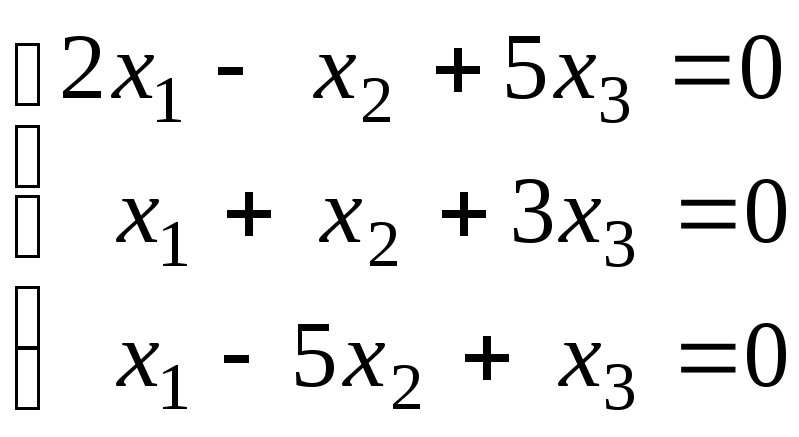 .
. -
С помощью союзной матрицы найти обратную для матрицы
 .
Проверить, что
.
Проверить, что


-
Методом Гаусса найти матрицу, обратную матрице
 , и с её помощью решить систему уравнений
, и с её помощью решить систему уравнений
 .
.
Вариант 2
-
Вычислить определитель:
 .
. -
По формулам Крамера решить систему уравнений :
 .
. -
Найти произведение матриц : а)
 б)
б)
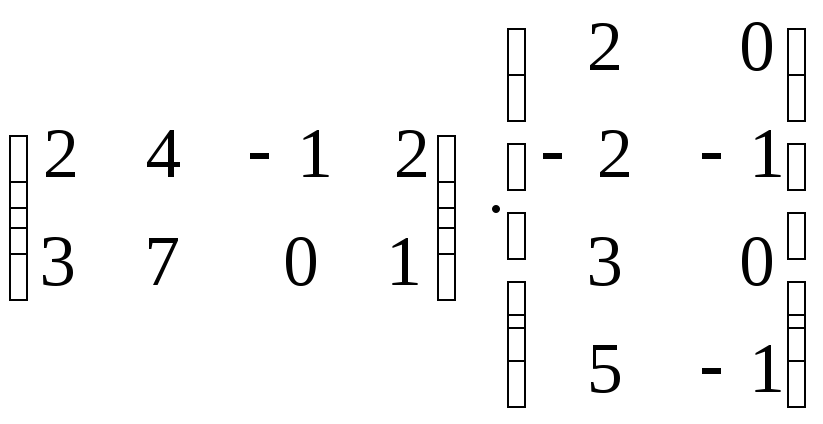
-
Методом Гаусса решить две системы уравнений с одной и той же матрицей :
 ,
,
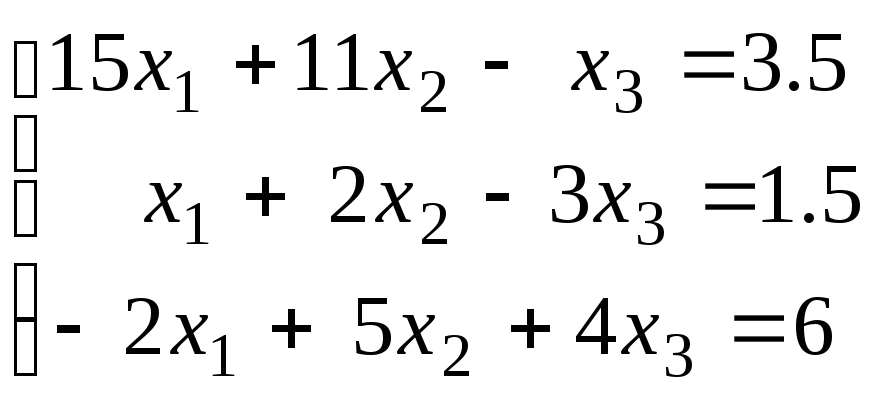 .
. -
Методом Гаусса решить систему и представить её решение в базисной форме :
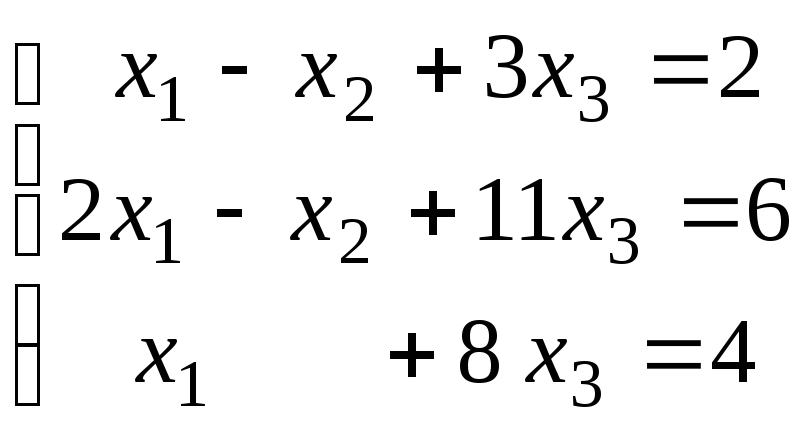 .
. -
Методом Гаусса решить однородную систему и представить её решение в базисной форме :
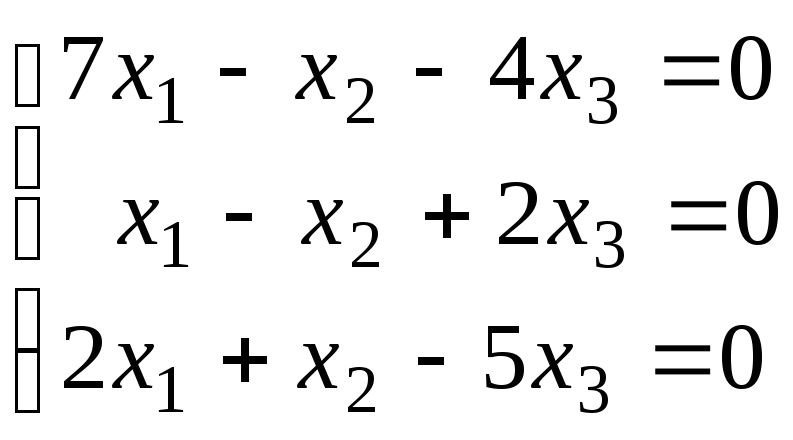 .
. -
С помощью союзной матрицы найти обратную для матрицы
 .
Проверить, что
.
Проверить, что


-
Методом Гаусса найти матрицу, обратную матрице
 , и с её помощью решить систему уравнений
, и с её помощью решить систему уравнений
 .
.
Вариант 3
-
Вычислить определитель:
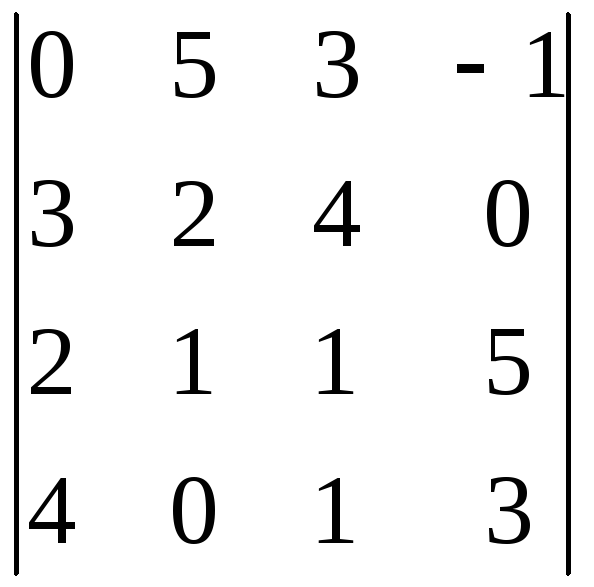 .
. -
По формулам Крамера решить систему уравнений :
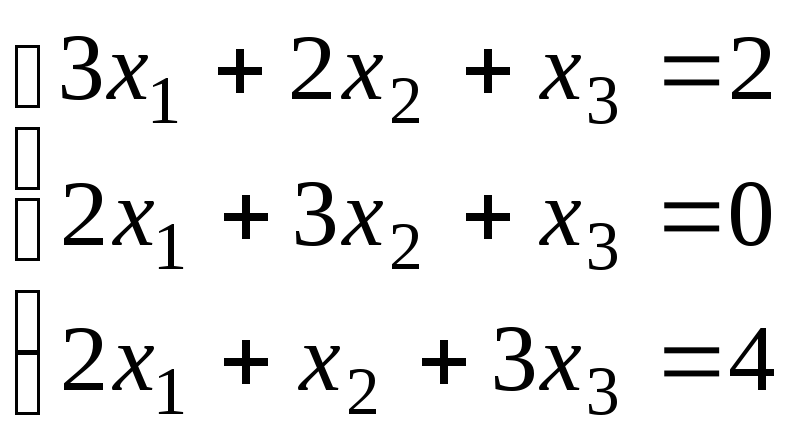 .
. -
Найти произведение матриц : а)
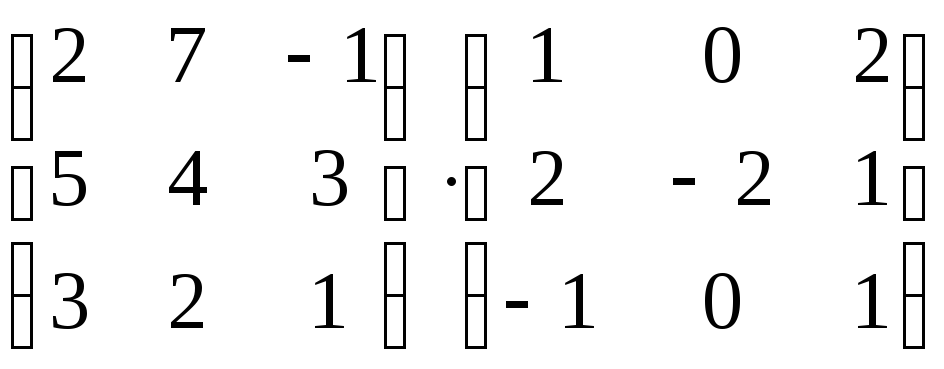 б)
б)
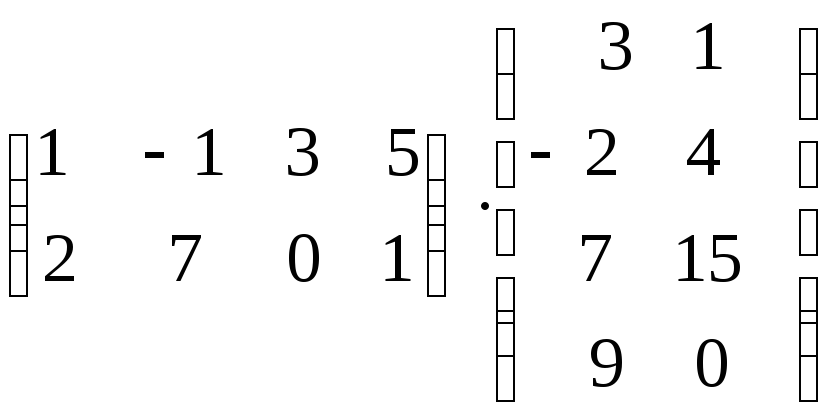
-
Методом Гаусса решить две системы уравнений с одной и той же матрицей :
 ,
,
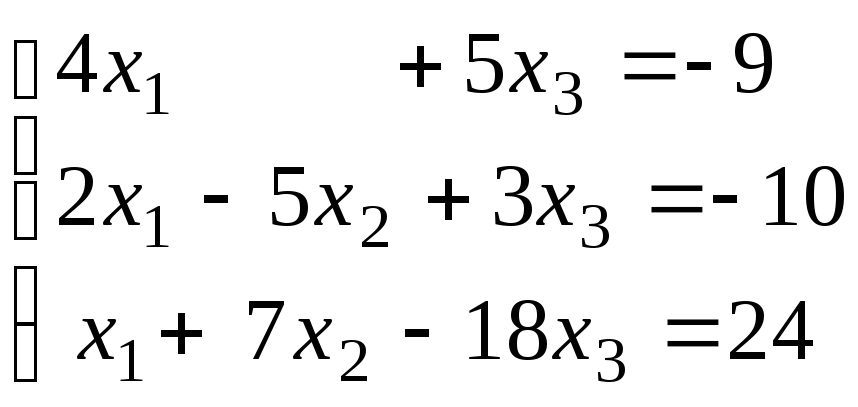 .
. -
Методом Гаусса решить систему и представить её решение в базисной форме :
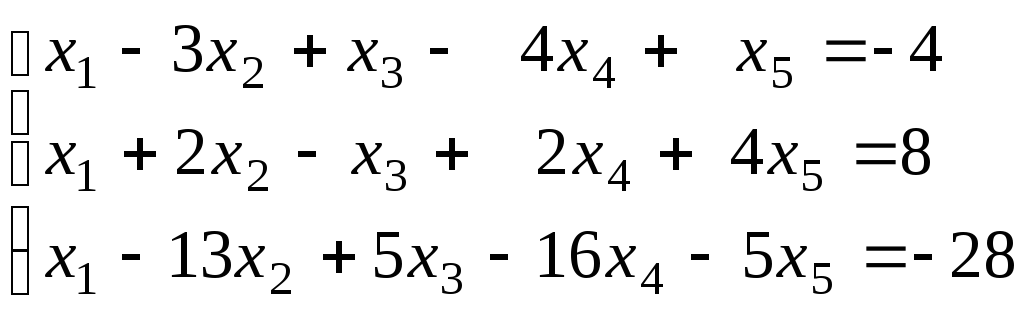 .
. -
Методом Гаусса решить однородную систему и представить её решение в базисной форме :
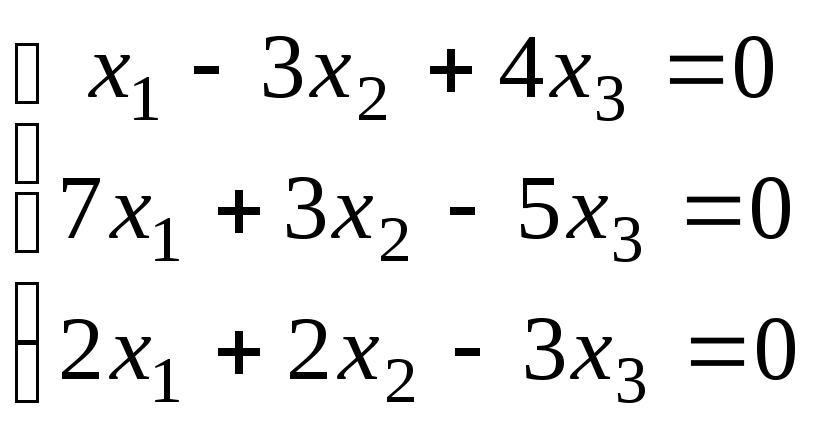 .
. -
С помощью союзной матрицы найти обратную для матрицы
 .
Проверить, что
.
Проверить, что


-
Методом Гаусса найти матрицу, обратную матрице
 , и с её помощью решить систему уравнений
, и с её помощью решить систему уравнений
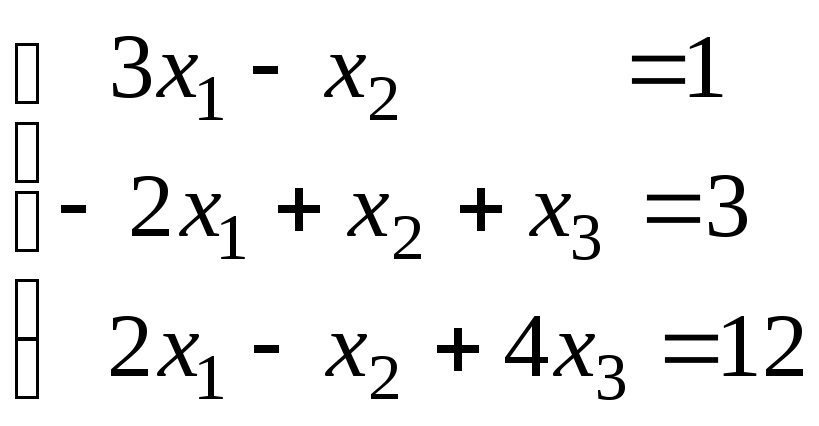 .
.
Вариант 4
-
Вычислить определитель:
 .
. -
По формулам Крамера решить систему уравнений :
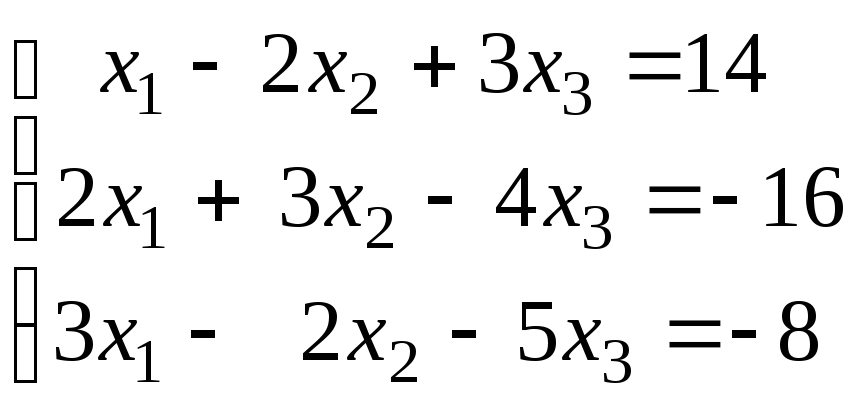 .
. -
Найти произведение матриц : а)
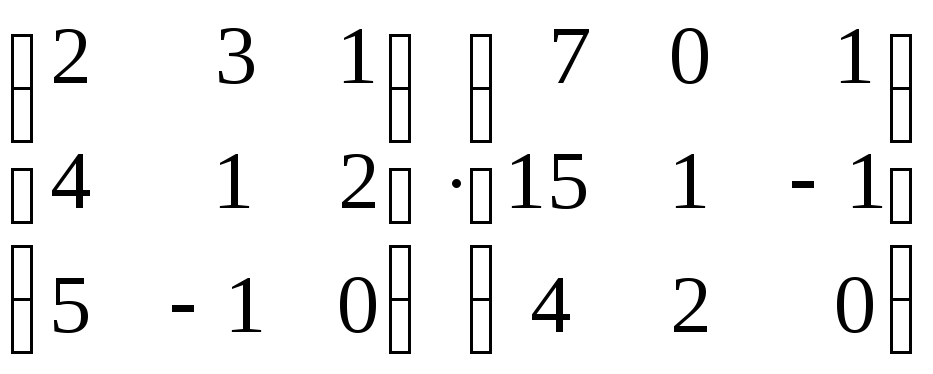 б)
б)
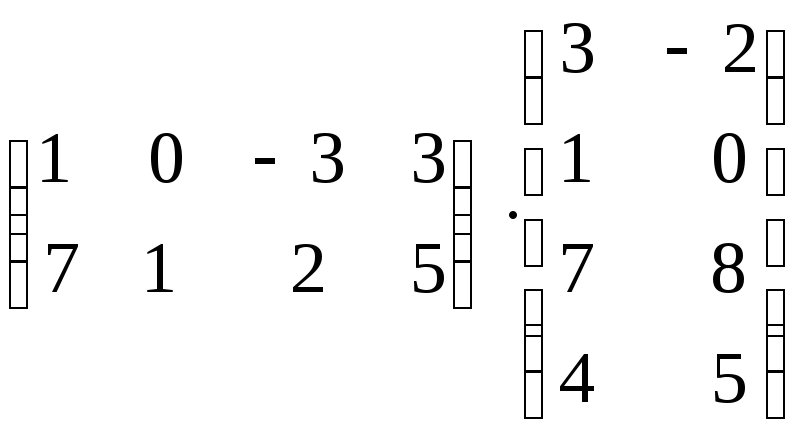
-
Методом Гаусса решить две системы уравнений с одной и той же матрицей :
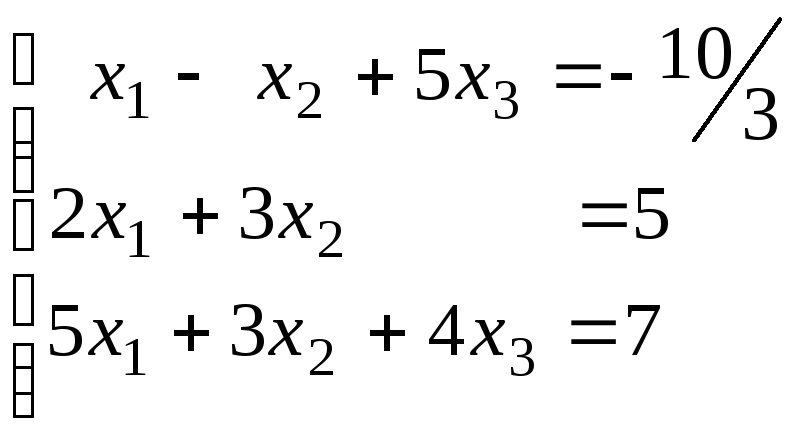 ,
,
 .
. -
Методом Гаусса решить систему и представить её решение в базисной форме :
 .
. -
Методом Гаусса решить однородную систему и представить её решение в базисной форме :
 .
. -
С помощью союзной матрицы найти обратную для матрицы
 .
Проверить, что
.
Проверить, что


-
Методом Гаусса найти матрицу, обратную матрице
 , и с её помощью решить систему уравнений
, и с её помощью решить систему уравнений
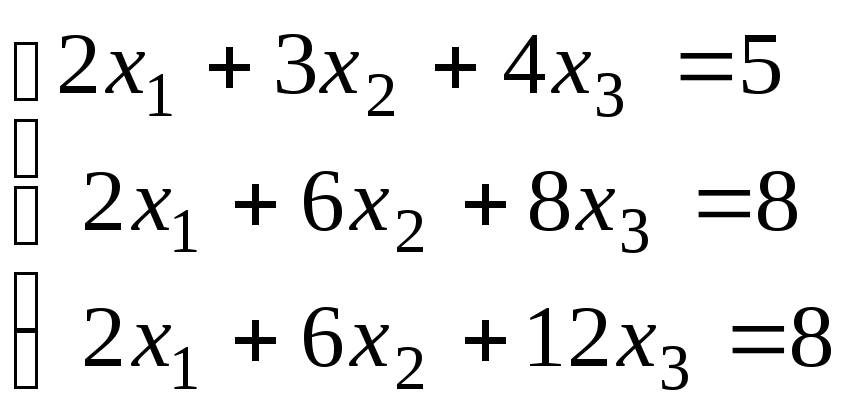 .
.
Вариант 5
-
Вычислить определитель:
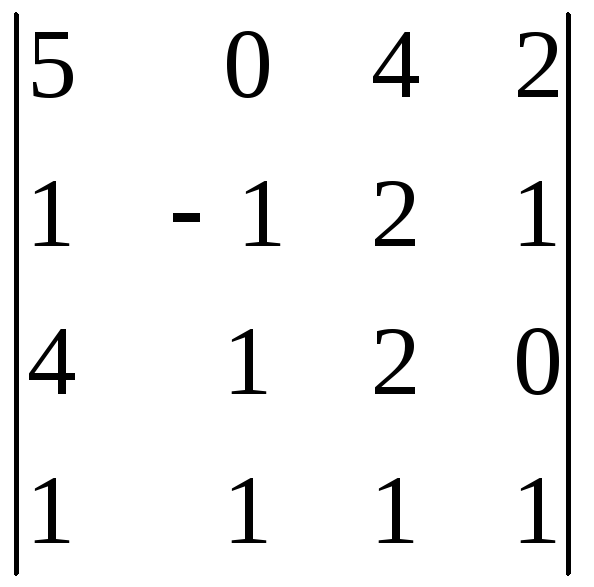 .
. -
По формулам Крамера решить систему уравнений :
 .
. -
Найти произведение матриц : а)
 б)
б)
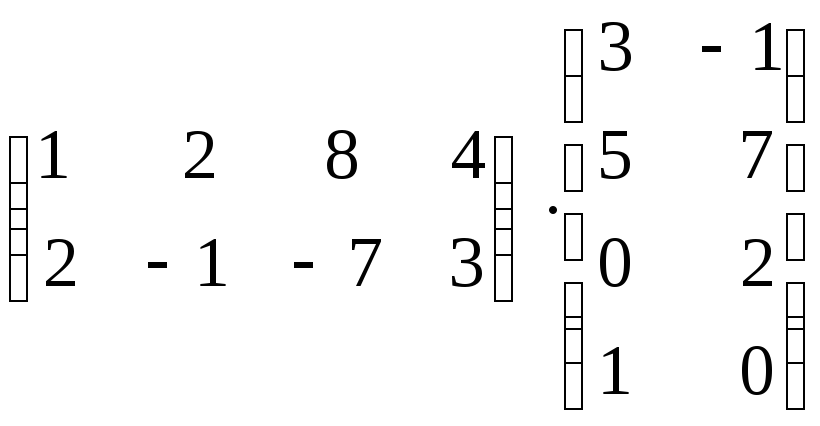
-
Методом Гаусса решить две системы уравнений с одной и той же матрицей :
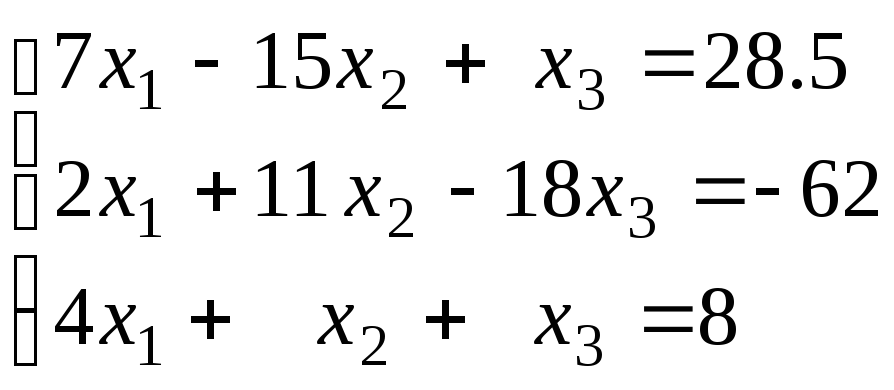 ,
,
 .
. -
Методом Гаусса решить систему и представить её решение в базисной форме :
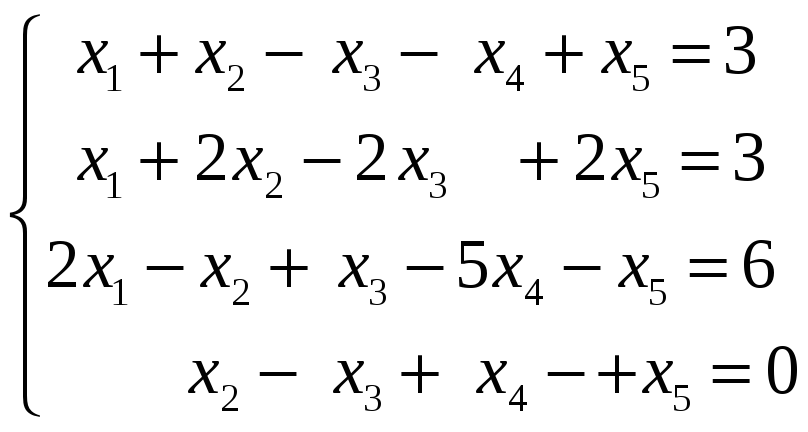 .
. -
Методом Гаусса решить однородную систему и представить её решение в базисной форме :
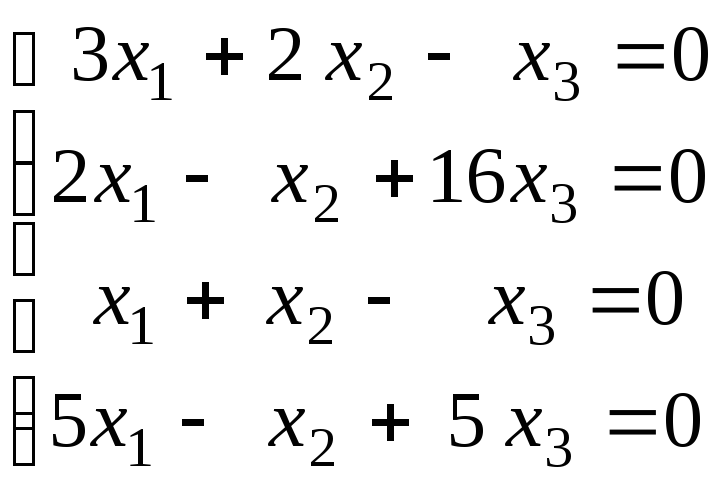 .
. -
С помощью союзной матрицы найти обратную для матрицы .
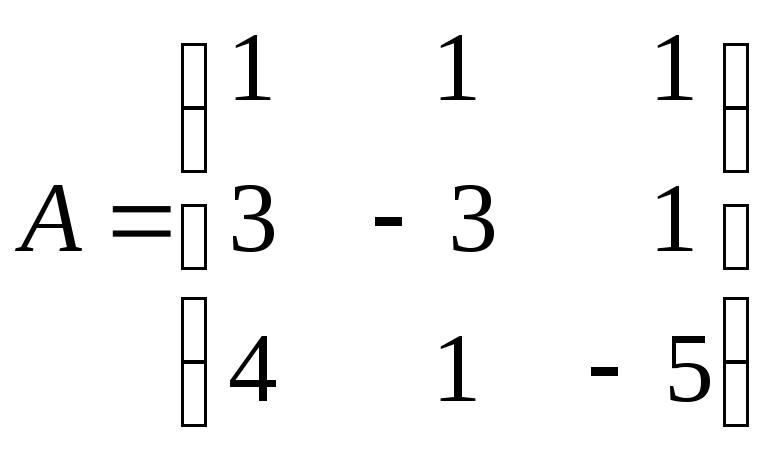 Проверить, что
Проверить, что


-
Методом Гаусса найти матрицу, обратную матрице
 , и с её помощью решить систему уравнений
, и с её помощью решить систему уравнений
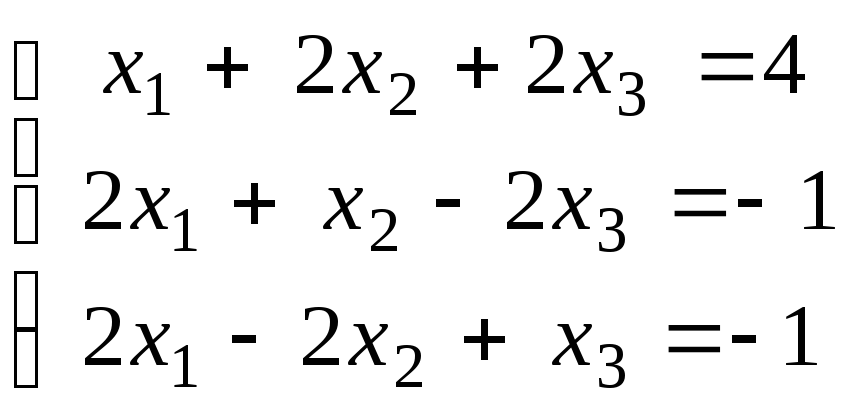 .
.
