Глава XI

^{Гиперграфы}

Гиперграф — это такое обобщение простого графа, когда ребрами могут быть не только двухэлементные, но и любые подмножества вершин. Подобные объекты в математике известны давно, однако введение термина «гиперграф» связано с успешным распространением на них ряда важных понятий и методов теории графов.

Отметим, что понятиями, близкими понятию «гиперграф», являются понятия сети (см. [32]) и блок-схемы см. [30]). Матроиды, которым посвящена гл. III, представляют собой специальный класс гиперграфов.

§ 68. Основные определения и свойства

Пусть V — конечное непустое множество, E — некоторое семейство непустых (необязательно различных) подмножеств множества V. Пара (V, Е) называется гиперграфом с множеством вершин V и множеством ребер Е. Заметим, что матроид естественно рассматривать как гиперграф, ребрами которого служат циклы этого матроида и только они. Свободный матроид превращается при этом в пустой, т. е. не имеющий ребер гиперграф, тривиальный матроид оказывается гиперграфом, ребра которого — все одноэлементные подмножества вершин.

Равные подмножества в Е называются кратными ребрами гиперграфа. Множество вершин и семейство ребер гиперграфа H обозначаются символами VH и EH соответственно. Число |VH| вершин гиперграфа H называется его порядком и обозначается через |Н|. Если |Н| = п, |EН|=т (с учетом кратности ребер), то H называется (п, т)-гиперграфом.

Если вершина v € V принадлежит ребру е € E, то будем говорить, что они инцидентны. Каждой вершине v € V гиперграфа H сопоставим множество E(v) всех инцидентных ей ребер. Число |E(v)| называется степенью вершины v, а |е| — степенью ребра е. Поскольку ребра­ми гиперграфа могут быть лишь непустые подмножества вершин, то степень любого ребра не меньше единицы, т. е. |е| > 1. Вершина гиперграфа, не инцидентная никакому ребру, называется изолированной.

Две вершиныv и v" гиперграфа Н назовем смежными, если существует ребро е =EН, которое содержит обе эти вершины.

Два ребра е' и е" гиперграфа Н назовем смеж­ными, если е’ ∩ е" ≠ ¢.

На рисунке ребро е удобно изображать сплошной ли­нией, окружающей все вершины из е, если |е| > 2 или |е| = 1, Если же |е| =2, то такое ребро е будем изо­бражать линией, соединяющей две вершины этого ребра, как и в случае обычных графов. На рис. 68.1 изображен гиперграф с множеством вершин V = { v₁, v₂ , ..., v₉} и множеством ребер E = {e₁= { v₁, v₂ ,v₃}, e₂ = { v₂, v₄ , v₅ ,v₆} ,е₃ = {v₆ ,v₇ ,v₈},e₄ ={ v₃ , v₈},e₅ = {v₉}, e₆ ={v₆}}.

Если в гиперграфе Н нет кратных ребер и степень лю­бого ребра е равна h (|е| = h), то гиперграф Н называет­ся h-однородным (h-униформным). Ясно, что всякий про­стой граф является 2-однородным гиперграфом. Тем са­мым граф — частный случай гиперграфа.

Любому (n, m)-гиперграфу Н =(V, E) без изолиро­ванных вершин можно сопоставить (m, п)-гиперграф Н* =(V*, E*), в котором V* =E, а E* — семейство всех множеств E(v), v € V. Гиперграф Н* называется двой­ственным к Н. На рис. 68.2 изображен гиперграф, двой­ственный к гиперграфу рис. 68.1.

Очевидно, что (Н *)*= Н для любого гиперграфа Н, не имеющего изолированных вершин.

Для любого гиперграфаН = (V, E) определим граф инциденций — двудольный граф К(Н) с множеством вершин V U &Е и множеством ребер {(v, e):(v, е) € V Х E,? € е}. Граф К(Н) называется кёниговым представлением гиперграфа Н. На рис. 68.3 изображено кёнигово представление К(Н) гиперграфа Н, приведенного на рис. 68.1.

Очевидно, что К(Н*) получается из К(Н) лишь переменой множеств V и E местами, причем все ребра сохраняются; таким образом, К(Н*) = К(Н).

В гиперграфе Н = (V, Е) цепью длины l>0 или (v_i , v_i+1)-цепью называется такая последовательность v₁ , e₁ , e₂, ..., e_l , v_l+1 , что:

1. все вершины v₁, v₂ , ..., v _{l +1}, кроме, возможно, крайних, различны;

2. e₁ , e₂,…., e_L — различные ребра Н;

3) v_i , v_i+1 € e_i для любого i = 1, l.

Здесь и далее под различными ребрами гиперграфа Н подразумеваются различные члены семейства ЕН (как подмножества они могут совпадать; например, на рис. 68.4 1 e₁ и e₂ — различные ребра).

Если l > 1 и v_l+1 = v₁ , то цепь называется циклом.

Заметим, что для соответствующих понятий графа мы добавили слово «простой» (простой цикл, простая цепь).

На рис. 68.4 v₂ , e₅ , v₅ , e₄ , v₇ , e₃ , v₈ и v₁ , e₁ , v₂ , e₂ , v₃ — цепи, a v₂ , e₁ , v₄ , e₃ , v₇ , e₄ , v₅ , e₅ , v₂,и v₁ , e₁ , v₂ , e ₅ , v₅ , e₄ , v₇ , e₃ , v₄ , e₂ , v₁ — циклы.

Очевидно, что существует биекция между цепями (циклами) гиперграфа H = (V, Е) и простыми цепями (простыми циклами) его кёнигова представления, концы которых принадлежат множеству V.

Пусть H = (V, E) — гиперграф, ¢ ≠ V’ € V. Подгиперграфом, порожденным множеством вершин V, называется гиперграф H’ = (V’, E’), где E' = { е' : = е’ = e ∩ V’ ≠ ¢ ,e € E}.

Вершины и и v гиперграфа Н называются связанны­ми, если и = v или в Н существует (и, v)-цепь. Легко

в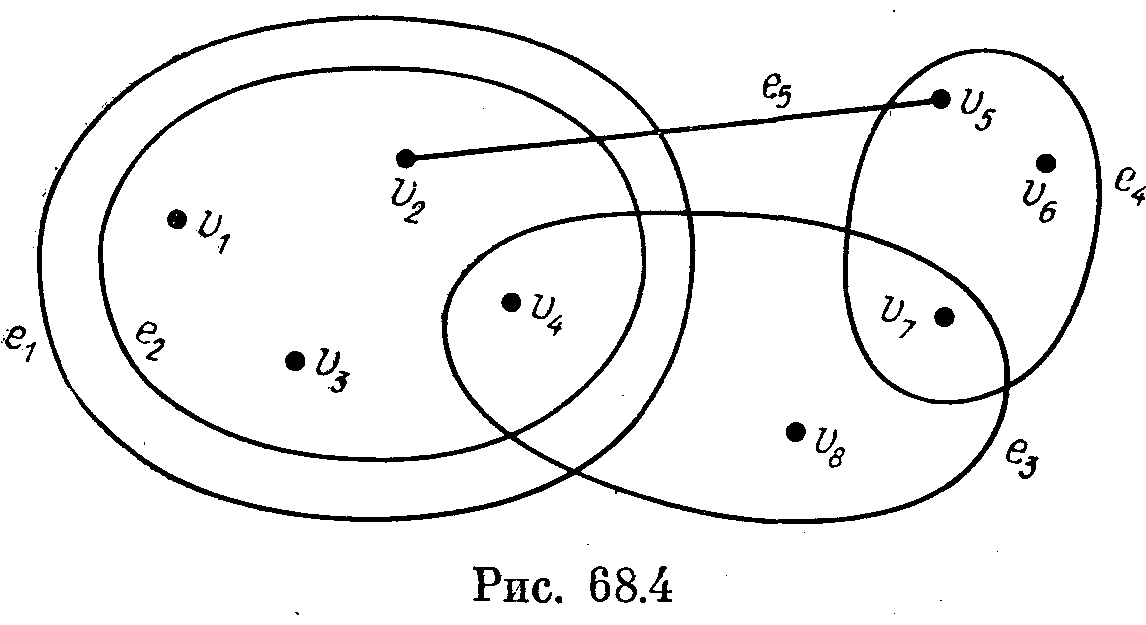идеть, что отношение связанности есть отношение экви­валентности на множестве вершин гиперграфа. Классы этого отношения называются областями связности гипер­графа Н, а порожденные областями связности подгиперграфы называются компонентами (связными компонен­тами) гиперграфа Н. Количество компонент гиперграфа Н обозначается через k(Н). Если k(Н)= 1, то гиперграф Н называется связным. Очевидно, что k(Н) = k(К(Н)), где k(К(Н)) — число компонент графа К(Н).

Утверждение 68.1. (n, т)-гиперграф Н не содержит циклов тогда и только тогда, когда

Очевидно, что гиперграф Н не содержит циклов тогда и только тогда, когда его кёнигово представление К(Н) является лесом. Но граф К(Н) имеет k(Н) компо­нент, m + п вершин и ∑ | e | ребер. Поэтому на осно­вании следствия 13.4 имеем

Утверждение 68.2. Гиперграф Н не содержит циклов тогда и только тогда, когда для любого непустого

подмножества Е’ € ЕH выполняется неравенство

Достаточность. Предположим, что Н содержит цикл v₁ , e₁ , v₂ , e₂ ,… , v_l , e_l. v₁ Тогда, положив E' = {e₁ , e₂,…., e_l}, имеем

то противоречит неравенству (1).

Необходимость. Если гиперграф Н = (V, E) не содержит цикла, то для любого Е' € Е гиперграф Н' =

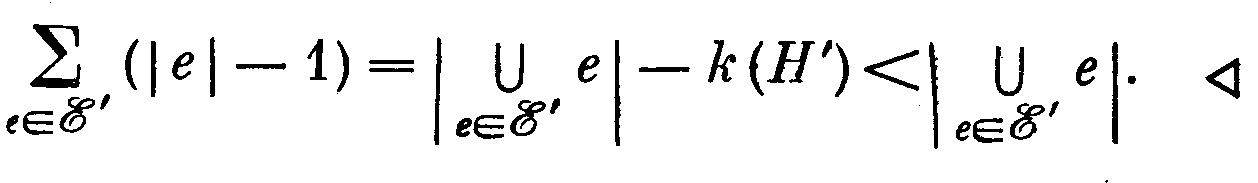(V’, E’) с множеством вершин V’ = U e также не содержит цикла. Поэтому на основании утверждения 68.1 имеем

Поскольку всякому циклу гиперграфа соответствует цикл в двойственном гиперграфе, то, применяя только что доказанный критерий к двойственному гиперграфу (разумеется, предварительно удалив изолированные вершины из исходного гиперграфа), получаем

Утверждение 68.3. Гиперграф Н не содержит циклов тогда и только тогда, когда для любого непустого подмножества V’ € V выполняется неравенство

Приведем без доказательства (его можно найти в [20]) еще один результат.

Теорема 68.4 (Л. Ловас, 1968). Если гиперграф Н порядка п не имеет циклов длины 1≥3, а |е|≥2и|e∩ е'| ≤ 2 для любых различных е, е’ € EН, то

Циклическим рангомv(H) гиперграфа Н называется циклический ранг его кёнигова представления К(Н):

Из этого определения в силу следствия 13.5 вытекает, что гиперграф имеет единственный цикл тогда и только тогда, когда v(H)= 1, т. е. когда ∑(|e| — 1) = n —k(H) + 1.

Кроме того, очевидно, что v(H *) = v(H).

Паросочетанием в гиперграфе Н называется подмноже­ство E’€ E , для любых двух различных ребер е’ и е" которого е’ ∩е" = ¢; таким образом, любые два ребра из E' не смежны.

Паросочетание называется наибольшим, если число ре­бер в нем максимально среди всех паросочетаний в Н. Число ребер в наибольшем паросочетаний гиперграфа Н называется числом паросочетания и обозначается через α1(H).

Пусть задано семейство S₁, S₂, ..., S_k непустых под­множеств конечного множества S. Трансвереальным мно­жеством этого семейства будем называть любое множе­ство Т € S, такое что Т ∩ S_i ≠ ¢ (i — 1, k). Трансверсальным множеством гиперграфа Н будем называть трансверсальное множество семейства его ребер. Таким образом, множество Т € VH является трансверсальным множест­вом гиперграфа Н, если для любого ребра е ≡ EH спра­ведливо соотношение Т ∩ е ≠ ¢.

Очевидно, что в случае, когда E' — наибольшее паро­сочетание в H, множество U e является трансверсальным множеством гиперграфа H.

Минимальное число вершин трансверсального множе­ства называется числом трансверсальности гиперграфа Н и обозначается τ(H).

Утверждение 68.5. Для любого гиперграфа В справедливо неравенство

Если Р — паросочетание в гиперграфе H, а Т — трансверсальное множество этого гиперграфа, то |Т| ≥| Р|. Отсюда имеем

где ГН — семейство всех трансверсальных множеств ги­перграфа Н, PH — множество всех паросочетаний в Н.

Число r(H) = max | е | называется рангом гиперграфа Н.

Утверждение 68.6. Для любого гиперграфа Н

Пусть Ро € EН — наибольшее паросочетание. Тогда |Po|=α1(H), a U e — трансверсальное множество гиперграфа Н. Поэтому