
§ 23. Жадный алгоритм
Рассмотрим следующую задачу дискретной оптимизации. Пусть Е — непустое конечное множество, w: E → R+ — функция, ставящая в соответствие каждому элементу е этого множества неотрицательное действительное число w(e)—вec элемента е. Для ХЕ вес w(X) определим как сумму весов всех элементов множества X:
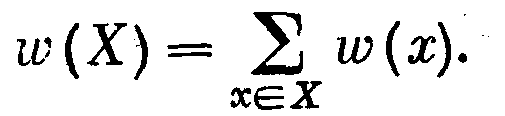
Пусть, далее, I — некоторый набор подмножеств множества Е, т. е. I 2E. Задача состоит в выборе в I подмножества максимального веса.
Оказывается, что в случае, когда I является набором независимых множеств матроида, эта оптимизационная задача решается с помощью следующего простого алгоритма.
Жадный (градиентный) алгоритм.
1-й шаг. Находим такой элемент е1 Е, что
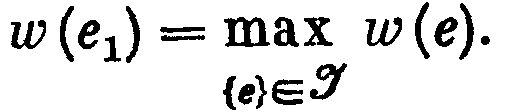
к-й шаг (к≥2). Находим такой элемент еk Е, что
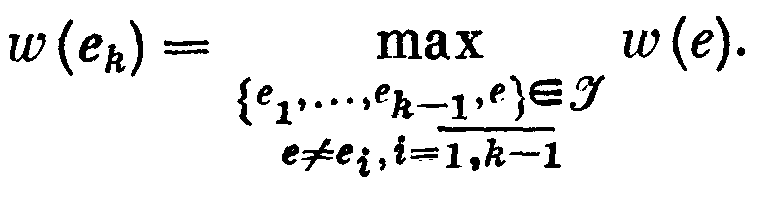 Если такого элемента
нет, то конец.
Если такого элемента
нет, то конец.
Примером жадного алгоритма служит алгоритм Краскала нахождения остова максимального веса во взвешенном графе (см. § 15).
Очевидно, что выходом жадного алгоритма всегда является элемент множества I, максимальный относительно включения. Однако он может оказаться не максимального веса. Чтобы убедиться в этом, рассмотрим пример: Е = {1, 2, 3}, I = {{1}, {1, 2}, {2, 3}}, w(1) = 3, w(2) = 2, w(3) = 4. Наш алгоритм найдет множество {1, 2}, хотя множество {2, 3} имеет больший вес.
Возникает вопрос: когда же можно гарантировать получение подмножества максимального веса, решая задачу с помощью жадного алгоритма? На этот вопрос отвечает следующая
Теорема 23.1. Если I — набор независимых множеств матроида М = (Е, I), элементам которого приписаны неотрицательные веса, то жадный алгоритм находит в I множество максимального веса.
> Очевидно, что жадный алгоритм строит базу; пусть это база
![]()
Остается
показать, что вес базы Во
максимален.
Пусть это
не так. Среди всех баз максимального
веса выберем такую
базу В,
которая
имеет наибольшее число общих элементов
с Во.
Так
как В ≠
Вo
и
|В|
=
|Bo|,
то Во\В
≠
Ø.
Выберем
в Bo\B
элемент
еi
с
минимальным номером i.
Множество
В
![]() еi
содержит
цикл С.
Так
как база
матроида циклов не содержит, то существует
eС\Во.
Пусть
В`
=(B\e)
еi
содержит
цикл С.
Так
как база
матроида циклов не содержит, то существует
eС\Во.
Пусть
В`
=(B\e)![]() еi.
Множество
В`
не
содержит циклов, поскольку С
—
единственный цикл в В
еi.
Множество
В`
не
содержит циклов, поскольку С
—
единственный цикл в В
![]() ei
(следствие
16.7). Кроме того, |В`|
= |В|.
Следовательно,
В`
является
базой. Далее имеем
ei
(следствие
16.7). Кроме того, |В`|
= |В|.
Следовательно,
В`
является
базой. Далее имеем
![]() Поэтому
Поэтому
 иное
противоречило бы выбору базы В.
иное
противоречило бы выбору базы В.
С другой стороны, w(B`)=w(B)—w(e)+w{ei), поэтому из (1) вытекает, что w(e)> w>(еi). Но последнее неравенство неверно, поскольку на i-м шаге алгоритм выбрал ei, а не е. Полученное противоречие доказывает теорему. <
Из приведенного выше доказательства вытекает, что жадный алгоритм можно трактовать как следующую процедуру получения базы максимального веса в матроиде: выбираем элементы матроида в порядке невозрастания весов, отвергая лишь те элементы, добавление которых нарушает условие независимости получаемых множеств.
Аналогично работает жадный алгоритм и для получения базы минимального веса, только при этом элементы матроида выбираются в порядке неубывания весов.
Заметим, что приведенное здесь доказательство предыдущей теоремы буквально то же, что и доказательство теоремы 15.1, обосновывающей алгоритм Краскала.
Оказывается, верна теорема, в некотором смысле обратная предыдущей.
Теорема
23.2. Пусть
F
—
набор
подмножеств конечного
множества Е, обладающий тем свойством,
что если XF,
У![]() Х,то
YF.
Тогда, если F
не является набором
независимых множеств матроида, то
применение к F
жадного алгоритма не гарантирует
получения подмножества
максимального веса.
Х,то
YF.
Тогда, если F
не является набором
независимых множеств матроида, то
применение к F
жадного алгоритма не гарантирует
получения подмножества
максимального веса.
>
Пусть для набора F
не
выполняется аксиома I.2,
т. е. в F
есть
такие Х
= {х1, х2, ...,
xk+1},
Y
= {y1,
y2,
..., yk),
что
не существует xi
Х\уi,
для
которого Y
![]() xi
e
F.
Покажем, что в этом случае можно так
подобрать веса,
что жадный алгоритм построит множество
не максимального
веса.
xi
e
F.
Покажем, что в этом случае можно так
подобрать веса,
что жадный алгоритм построит множество
не максимального
веса.
Пусть
w(уi)=1
(i
= 1,…,k),
w(xi)=t,
если
xi
Х\Y,
где 0<t<1,
w(е)
= 0, если е
Е\(X![]() Y),
Тогда жадный
алгоритм построит сперва множество Y.
Так как отсутствует
такой элемент xi,
что
Y
Y),
Тогда жадный
алгоритм построит сперва множество Y.
Так как отсутствует
такой элемент xi,
что
Y![]() xi
F,
то далее алгоритм выберет элементы
из Е\(Х
xi
F,
то далее алгоритм выберет элементы
из Е\(Х![]() Y)
и закончит работу, получив
в результате множество Хо, вес которого
равен весу
множества Y.
Y)
и закончит работу, получив
в результате множество Хо, вес которого
равен весу
множества Y.
Пусть |Х∩Y|=р. Тогда w(X) = p-{k+1-p)t. Поэтому, учитывая, что w (Хо) = k, можно выбрать 0 < t < 1 таким, чтобы было w(Xo)<w(X). Тем самым жадный алгоритм не находит в F множества максимального веса. <
