
§ 18. Примеры матроидов
Рассмотрим некоторые примеры матроидов.
1. Пара (Е, {E}), где Е — конечное непустое множество, является матроидом, единственной базой которого служит само множество Е. Этот матроид называется свободным (или дискретным). Циклов свободный матроид не имеет, всякое подмножество Х Е независимо, а (Х)=|Х|.
Двойственный к свободному — тривиальный матроид (Е, { Ø }), единственной базой которого является пустое множество. Очевидно, что Ø служит единственным независимым множеством тривиального матроида; его циклы — все одноэлементные подмножества множества Е; (X) = 0 для любого Х Е.
2. Пусть L — линейное пространство над произвольным полем F, E L — конечное непустое подмножество, I — множество, элементами которого служат все линейно независимые над F системы векторов из Е и пустое множество. Тогда пара (Е, I) является матроидом с набором независимых множеств I (этот факт вытекает из известной в линейной алгебре теоремы Штейница о замене). Такой матроид называется векторным матроидом, порожденным множеством векторов Е. Базами этого матроида служат все базы множества Е. Если же в Е нет баз, т. е. если Е = {0}, то единственной базой векторного матроида является пустое множество, т. е. он тривиален. Ранг векторного матроида равен рангу множества Е, т. е. размерности подпространства, порожденного множеством Е.
В частности, взяв в качестве Е множество векторов, являющихся столбцами (строками) какой-либо матрицы А, получим матричный матроид, или матроид столбцов (строк) матрицы А. Ранг этого матроида равен рангу матрицы А.
В качестве иллюстрации рассмотрим матроид M столбцов матрицы
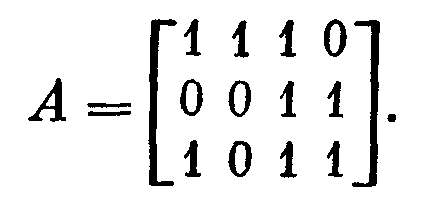
Обозначив
i-й
столбец
этой
матрицы
через
ei
(i=1,2,3,4),
получим
Е
= {е1,
e2, e3,
e4}, ρ(М)
= rank
A
= 3.
Перебирая
все
максимальные линейно независимые
системы столбцов
матрицы А,
обнаружим,
что матроид М
имеет
ровно 3
базы: B1
={e1,
e2,
e3},
B2
={e1,
e2,
e4),
B3
= {e1,
e3,
e4}.
Зависимых множеств 2: Е
и
{e2,
е3,
e4},
причем
последнее множеству
служит единственным циклом матроида
М.
Кобазы:
![]() 1
= {е4},
1
= {е4},
![]() 2
=
{е3},
2
=
{е3},
![]() 3
=
{e2}.
Козависимые множества:
{е1}
и
каждое подмножество в Е,
содержащее
более
одного элемента. Коциклы: {е1},
(е2,
е3},
{е2,
e4},
{е3,
е4}.
3
=
{e2}.
Козависимые множества:
{е1}
и
каждое подмножество в Е,
содержащее
более
одного элемента. Коциклы: {е1},
(е2,
е3},
{е2,
e4},
{е3,
е4}.
3. Пусть G — произвольный граф. Определим матроид M(G) = (E, β) на множестве E = EG, объявив базами множества ребер всех остовов графа G, т. е. β = {ЕН: Н—остов G). Из утверждения 13.8 вытекает, что аксиомы баз в этой ситуации действительно выполняются. Поскольку каждый подграф графа G, являющийся лесом, содержится в некотором остове (утверждение 13.7), то независимыми множествами в M(G) служат множества ребер подграфов в G, являющихся лесами, и только они. Циклы матроида M(G) — это множества ребер простых циклов графа G. Если n(G), m(G), к(G) — числа вершин, ребер и компонент графа G соответственно, то
 т.e.
ранг и коранг матроида M(G)
равны,
соответственно, коциклическому рангу
и циклическому рангу графа G.
т.e.
ранг и коранг матроида M(G)
равны,
соответственно, коциклическому рангу
и циклическому рангу графа G.
Если В — множество всех ребер какого-либо остова графа G, то множество EG\B называется коостовом. Подмножество UEG называется разделяющим множеством графа G, если число компонент графа G – U больше, чем число компонент G. Минимальное относительно включения разделяющее множество называется разрезом. Кобазами в M(G) служат коостовы графа G. Из утверждения 17.2 непосредственно вытекает, что козависимые множества в M(G) — это разделяющие множества графа G, а коциклы — это разрезы. Поэтому между свойствами простых циклов и разрезов графа существует большая аналогия. Эта аналогия и явилась одной из причин возникновения понятия «матроид».

Матроиды M(G) и M*(G) называются матроидом циклов {циклическим матроидом) и матроидом разрезов (коциклическим матроидом) графа G соответственно.
Рассмотрим,
например, циклический матроид M(G)
графа
G,
изображенного
на рис. 18.1. Для этого матроида Е
= {е1,
е2,
е3,
е4}.
Он
имеет ровно три базы: В1
= {е1, е2,
е4}, В2
=
{e1,
е3, е4}, В3
= {е2,
е3, e4}.
Единственным его циклом служит множество
{е1,
е2,
е3}. Кобазы:
![]() 1
=
{е3},
1
=
{е3},
![]() 2
= {е2},
2
= {е2},
![]() 3
= {е1); коциклы:
{е1, е2}, {е1,
е3},
{е2, е3}, (e4}.
3
= {е1); коциклы:
{е1, е2}, {е1,
е3},
{е2, е3}, (e4}.
Очевидно, что для любого дерева Т циклический матроид М(Т) свободен, а М*(Т) тривиален.
Вернемся к произвольным графам. Применяя установленные выше утверждения о свойствах баз, независимых множеств и циклов матроида к матроидам M(G) и M*(G), получим следующие утверждения о графах. Каждое из них несложно доказать непосредственно, однако здесь вскрывается их общая сущность.
Утверждение 18.1. Пусть F и Н — ациклические подграфы графа G и |EF|<|EH|. Тогда существует такое подмножество ХЕН, что граф F` = F + X также является ациклическим и |EF`| = |ЕН|.
Утверждение
18.2. Если
D1
и D2
— несовпадающие
разрезы в графе G,
имеющие общее ребро е, то множество
ребер (D1
![]() D2)\e
является
разделяющим.
D2)\e
является
разделяющим.
Утверждение 18.3. Для любого непустого ациклического подграфа F графа G существует разрез в G, имеющий с F ровно одно общее ребро.
Утверждение 18.4. Число общих ребер любого простого цикла и любого разреза графа отлично от 1.
Замечание. Очевидно, что в формулировках утверждений 18.1—18.4 может фигурировать произвольный псевдограф, а не только простой граф.
