
Глава III
Матроиды и трансверсали
В этой главе вводится новый комбинаторный объект — матроид, появляющийся в результате обобщения хорошо известного читателю понятия линейной зависимости. Хотя понятие «матроид» возникло относительно давно,— в 30-е годы нашего столетия (впервые это понятие ввел Уитни) — место теории матроидов в математике и, тем более, в математическом образовании первоначально не было осознано. Теперь же, когда открываются все новые и новые классы матроидов, объединяющая роль идеи матроида, позволяющая с возрастающим успехом применять к решению комбинаторных проблем методы алгебры, становится все более ясной.
Для нас матроиды интересны, прежде всего, по двум причинам. Первая — их связь с теорией графов. Фактически, именно соответствие между некоторыми теоретико-графовыми и алгебраическими понятиями привело к созданию теории матроидов. Вторая причина состоит в том, что задачи оптимизации на матроидных структурах решаются с помощью простого, так называемого «жадного» алгоритма, который является обобщением алгоритма Краскала для нахождения остовного дерева минимального веса в связном взвешенном графе (§ 15). «Жадный» алгоритм изучается в этой главе.
§ 16. Азбука теории матроидов
Известно несколько эквивалентных друг другу определений матроида. Эти определения различаются тем, что учитывают различные свойства независимости. Начнем с определения, основанного на свойствах максимальных независимых множеств – баз.
Матроидом М называется пара (E, β), где E— конечное непустое множество, а β (или β (М))—непустое множество его подмножеств (называемых базами), удовлетворяющее следующим двум условиям (аксиомы баз).
В.1. Никакая из баз не содержится в другой базе.
В.2.
Если
B1
и
B2
–
базы, то для любого элемента b
B1
существует
такой элемент с
из
В2,
что
(В1\b)
![]() с – также
база.
с – также
база.
Элементы множества Е называются элементами матроида М. Число |Е| называется порядком матроида М.
Понятие матроида является естественным обобщением понятия линейной независимости. А именно, если Е – конечная система векторов некоторого линейного пространства, содержащая ненулевой вектор, то в Е существует максимальная линейно независимая подсистема –база системы Е. Напомним, что все базы системы Е удовлетворяют аксиомам баз В.1 и В.2. Следовательно, всякая такая система вместе с ее базами является матроидом. Этот матроид называется векторным.
Очевидно, что в обозначениях аксиомы В.2 либо b B2 и тогда можно взять с = b, либо с В2\В1, иное противоречило бы аксиоме В.1. Поэтому совокупность аксиом В.1 и В.2 равносильна совокупности аксиом В.1 и
В`.2.
Если В1,
B2
β
и
b
B1\B2,
то
в B2\B1
существует
такой элемент с, что (B1\b)\
![]() с
β.
с
β.
Утверждение 16.1. Все базы матроида равномощны.
> Пусть B1 и В2– базы, |В1| ≤ |В2| и В1 = {b1, b2,…, bρ}. Согласно аксиоме В.2 в базе В2 существует такой элемент c1, что
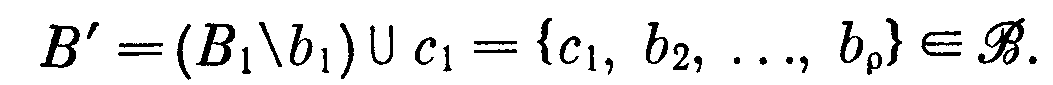
Далее, существует такой элемент с2 B2, что
![]() Итерируя
этот процесс, получим базу В
= (с1, с2, ...,
сρ),
являющуюся
подмножеством в В2
и
потому совпадающую
с В2
в
силу В.1. Следовательно, |В2|
=
ρ.
<
Итерируя
этот процесс, получим базу В
= (с1, с2, ...,
сρ),
являющуюся
подмножеством в В2
и
потому совпадающую
с В2
в
силу В.1. Следовательно, |В2|
=
ρ.
<
Мощность базы матроида М назовем его рангом и обозначим через ρ (М).
Любое подмножество базы матроида называется независимым. В частности, пустое множество независимо. Совокупность всех независимых подмножеств элементов матроида М обозначим через I(М) (или просто I). Ниже множество I(М) называется набором независимых множеств матроида М.
Очевидно, что β(М) совпадает с множеством элементов из I(M), максимальных относительно включения, так что множества β (М) и I (М) определяют друг друга.
Теорема 16.2. Набор I (М) независимых множеств матроида удовлетворяет следующим двум условиям (аксиомы независимости).
I.1. Если ХI(М), YX, то УI (М).
I`.2.
Если
X,
YI
(M)
и |Х| <
|Y|,
то
в Y\X
существует
такой элемент у, что X
![]() у
I
(M).
у
I
(M).
> Справедливость
условия 1.1 очевидна; рассмотрим условие
1.2. Пусть X,
YI
(M)
и
|Х|
<
|Y|.
Пусть,
далее,
B1
β
(M),
YB1.
Среди
баз, содержащих X,
выберем
такую базу В2,
чтобы
пересечение В1
∩
B2
содержало
наибольшее число элементов. Докажем,
что B2\XB1.
Действительно,
если бы существовал элемент b
В2\Х,
b![]() В1,
то
по аксиоме В.2 в базе В1
нашелся
бы такой элемент
z,
что C
= (B2\b)
В1,
то
по аксиоме В.2 в базе В1
нашелся
бы такой элемент
z,
что C
= (B2\b)
![]() z
β
(M).
Но
тогда |C∩B1|
>
|B2∩B1|,
что
невозможно. Следовательно, В2\Х
и
У содержатся
в В1,
причем
|В2\Х|
+ |Y|
=
ρ(М) — |X|
+ |Y|
>
ρ
(M)=|B1|.
Тем
самым существует у
(В2\Х)∩Y.
Поскольку
X
z
β
(M).
Но
тогда |C∩B1|
>
|B2∩B1|,
что
невозможно. Следовательно, В2\Х
и
У содержатся
в В1,
причем
|В2\Х|
+ |Y|
=
ρ(М) — |X|
+ |Y|
>
ρ
(M)=|B1|.
Тем
самым существует у
(В2\Х)∩Y.
Поскольку
X
![]() у
В2,
то
элемент у
–
искомый.
у
В2,
то
элемент у
–
искомый.
Очевидно, что аксиома I.2 эквивалентна следующей аксиоме.
I`.2.
Если
X,
YI
(M)
и |Х|
<
|Y|,
то
в Y
существует
такое подмножество Z,
что X![]() ZI
(M),
|X
ZI
(M),
|X![]() Z|
=
|Y|.
Z|
=
|Y|.
Следующая теорема показывает, что в основу определения матроида можно положить не базы, а независимые множества.
Теорема 16.3. Пусть Е — конечное непустое множество, I — непустая совокупность его подмножеств, удовлетворяющая аксиомам независимости I.1 и I.2, β — множество всех элементов из I, максимальных относительно включения. Тогда β удовлетворяет аксиомам баз В.1 и В.2.
> Очевидно, что β есть множество всех элементов из I максимальной мощности. Пусть теперь В1, В2 β, е1В1. Тогда B1\e1 I, |B1\e1| = |В2| - 1. Следовательно, существует такой элемент е2В2, что
 Из
последнего равенства вытекает, что B3
β.
Тем самым
доказано, что выполняется условие В.2.
Справедливость
условия В.1 очевидна. <
Из
последнего равенства вытекает, что B3
β.
Тем самым
доказано, что выполняется условие В.2.
Справедливость
условия В.1 очевидна. <
Предыдущая теорема дает основание для нового определения матроида. Матроидом назовем пару (Е, I), где Е — множество, а I — непустая совокупность его подмножеств (называемых независимыми), удовлетворяющих аксиомам независимости I.1 и I.2. Множество I назовем набором независимых множеств матроида. Максимальные относительно включения независимые подмножества назовем теперь базами матроида. Аксиомы баз при этом действительно будут выполняться. В этом смысле приведенные два определения матроида эквивалентны.
Определим ранговую функцию (функцию ранга) матроида М, ставящую в соответствие каждому подмножеству А Е число, равное максимальной из мощностей входящих в А независимых подмножеств и называемое рангом множества А: ρ (A) = max{|X|: ХА, ХI (М)}.
Очевидно, что ρ (E) совпадает с определенным выше рангом ρ(М). Очевидно также, что подмножество АЕ независимо тогда и только тогда, когда ρ(А)=|А|.
Теорема 16.4. Ранговая функция матроида удовлетворяет следующим трем условиям (аксиомы ранга):
 > Первые два
условия очевидны, рассмотрим третье.
Пусть
А,В
Е,
а
X
— наибольшее
по числу элементов независимое
подмножество в А
∩
В.
Согласно
условию I`.2
в
A
> Первые два
условия очевидны, рассмотрим третье.
Пусть
А,В
Е,
а
X
— наибольшее
по числу элементов независимое
подмножество в А
∩
В.
Согласно
условию I`.2
в
A
![]() В
существует
наибольшее по числу элементов независимое
подмножество Y,
содержащее
X.
Представим
Y
в виде Y
= X
В
существует
наибольшее по числу элементов независимое
подмножество Y,
содержащее
X.
Представим
Y
в виде Y
= X![]() V
V![]() W,
где
VA\B,
WB\A.
Независимое
подмножество X
W,
где
VA\B,
WB\A.
Независимое
подмножество X![]() V
содержится
в А,
поэтому
ρ
(A)
≥ |Х
V
содержится
в А,
поэтому
ρ
(A)
≥ |Х
![]() V|.
Аналогично
ρ
(B)
≥ |X
V|.
Аналогично
ρ
(B)
≥ |X
![]() W|.
Следовательно,
ρ
(A)
+ ρ
(B)
≥ |X
W|.
Следовательно,
ρ
(A)
+ ρ
(B)
≥ |X![]() W|
+|X
W|
+|X![]() W|.
Поскольку
X∩V
= X∩W
= Ø, то
далее имеем ρ(А)
+ ρ
(В)
≥
|X|
+
(|X|
+
|V|
+ |W|).
Но
|Х|=
ρ
(A∩B),
|X|
+ |V|
+ |W|
=
|Y|=
ρ(A
W|.
Поскольку
X∩V
= X∩W
= Ø, то
далее имеем ρ(А)
+ ρ
(В)
≥
|X|
+
(|X|
+
|V|
+ |W|).
Но
|Х|=
ρ
(A∩B),
|X|
+ |V|
+ |W|
=
|Y|=
ρ(A
![]() В).
В).
Итак,
ρ
(А) + ρ
(В)
≥ ρ
(A
![]() В)
+ ρ
(А
∩
В).
<
В)
+ ρ
(А
∩
В).
<
Подмножество А из Е называется зависимым, если оно не является независимым. Минимальное относительно включения зависимое множество называется циклом. Очевидно, что подмножество множества Е независимо тогда и только тогда, когда оно не содержит циклов.
Множество циклов матроида М обозначим через φ(М) (или просто φ).
Теорема 16.5. Если М — матроид, то множество φ(М) удовлетворяет следующим двум условиям (аксиомы циклов).
С.1. Ни один из циклов не содержится в другом цикле.
C.2.
Если
C1
и С2 —
несовпадающие
циклы и еС1
∩
С2,
то множество (С1![]() С2)\е
также содержит цикл.
С2)\е
также содержит цикл.
>
Выполнимость условия С.1 очевидна,
рассмотрим условие C.2.
Пусть D
= (C1
![]() C2)\е.
Достаточно доказать, что множество D
зависимо.
Прибегнем к помощи ранговой функции;
в ее терминах нужно доказать неравенство
ρ(D)
≤ |D|.
Но
D
C1
C2)\е.
Достаточно доказать, что множество D
зависимо.
Прибегнем к помощи ранговой функции;
в ее терминах нужно доказать неравенство
ρ(D)
≤ |D|.
Но
D
C1![]() C2,
и
потому ρ(D)
≤ ρ
(C1
C2,
и
потому ρ(D)
≤ ρ
(C1
![]() C2).
Согласно
аксиоме ρ.З
C2).
Согласно
аксиоме ρ.З
ρ
(С1![]() С2)
≤
ρ
(С1) + ρ
(С2)-
ρ
(С1 ∩
С2).
С2)
≤
ρ
(С1) + ρ
(С2)-
ρ
(С1 ∩
С2).
Очевидно, что ρ (Ci)= |Ci| - 1 для цикла Ci. Так как множество С1 ∩ С2 независимо, то ρ(C1 ∩ С2)= |С1 ∩ С2|.
Итак,
ρ
(D)
≤
ρ
(C1
![]() С2)
≤
|C1|
- 1 + |С2|
- 1
- |C1
∩
С2|
= |C1
С2)
≤
|C1|
- 1 + |С2|
- 1
- |C1
∩
С2|
= |C1
![]() С2| - 2
С2| - 2
и |D|
= |C1
![]() С2| -1, а значит, ρ
(D)<
|D|.
<
С2| -1, а значит, ρ
(D)<
|D|.
<
Заметим, что совокупность аксиом ρ.1 — ρ.З (как и C.1, C.2) можно использовать для еще одного определения матроида.
Следствие
16.6. Если
М = (Е, I)
— матроид с набором независимых
множеств I,
ХI,
y
Е,
то множество X
![]() у
содержит не более одного цикла.
у
содержит не более одного цикла.
> Пусть,
напротив, в X
![]() у
есть
два несовпадающих цикла
С1
и
С2.
Элемент
у
содержится
в каждом из них, и,
согласно предыдущей теореме, существует
третий цикл С
в
множестве D
=
(C1
у
есть
два несовпадающих цикла
С1
и
С2.
Элемент
у
содержится
в каждом из них, и,
согласно предыдущей теореме, существует
третий цикл С
в
множестве D
=
(C1
![]() С2)\у.
Следовательно,
D
—
зависимое множество. Но DX
и
потому независимо. Полученное противоречие
доказывает нужное утверждение. <
С2)\у.
Следовательно,
D
—
зависимое множество. Но DX
и
потому независимо. Полученное противоречие
доказывает нужное утверждение. <
Очевидно, что из предыдущего следствия вытекает
Следствие
16.7. Для
любой базы В матроида и любого
его элемента е, не входящего в эту базу,
множество
В ![]() е
содержит ровно один цикл.
е
содержит ровно один цикл.
