мат анализ

Статическим моментом S_x системы материальных точек относительно оси Ох называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси Ох):

Аналогично определяется статический момент S_y этой системы относительно оси

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

Пусть у = ƒ(х) (a≤x≤b) — это уравнение материальной кривой АВ. Будем считать ее однородной с постоянной линейной плотностью  ( = const).

Для произвольного х є [а; b] на кривой АВ найдется точка с координатами (х;у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна dl. Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dS_x («элементарный момент») будет равен dly, т. е. dS_x = dlу (см. рис. 196).

Отсюда следует, что статический момент S_x кривой АВ относительно оси Ох равен

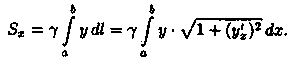
Аналогично находим S_y:

 Статические моменты S_x и S_y кривой позволяют легко установить положение ее центра тяжести (центра масс).

Центром тяжести материальной плоской кривой у = ƒ(х), х  [a;b] называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу m заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = ƒ (х) относительно той же оси. Обозначим через С(х_с;у_с) центр тяжести кривой АВ.

Из определения центра тяжести следуют равенства  Отсюда или

Пример 41.14. 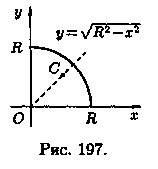Найти центр тяжести однородной дуги окружности x²+y²=R², расположенной в первой координатной четверти (см. рис. 197).

Решение: Очевидно, длина указанной дуги окружности равна πR/2, т. е. l=πR/2. Найдем статический момент ее относительно оси Ох. Так как уравнение дуги есть

Стало быть,

Так как данная дуга симметричнаотносительно биссектрисы первого координатного угла, то х_с=у_с=2R/π. Итак, центр тяжести имеет координаты

 

Вычисление статических моментов и координат центра тяжести плоской фигуры

Пусть дана материальная плоская фигура (пластинка), ограниченная кривой у = ƒ(х)  0 и прямыми у = 0, х = a, x = b (см. рис. 198).

Б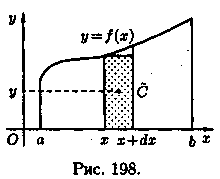удем считать, что поверхностная плотность пластинки постоянна ( = const). Тогда масса «всей пластинки равна  * S, т. еВыделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.

Тогда масса его равна ydx. Центр тяжести С пря моугольника лежит на пересечении диагоналей прямоугольника. Эта точка С отстоит от оси Ох на 1/2*у, а от оси Оу на х (приближенно; точнее на расстоянии х+¹/₂∆х). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения

Следовательно,

По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через С(х_с; у_с), что m•х_с=S_y, m•у_с=S_x. Отсюда

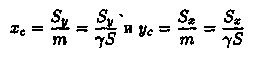
или

Пример 41.15. Найдем координаты центра тяжести полукруга х²+у²≤R², у≥0 (=const) (см. рис. 199).

Решение: Очевидно (ввиду симметрии фигуры относительно оси Оу), что х_с=0. Площадь полукруга равнаНаходим S_x:

Стало быть,

Итак, центр тяжести имеет координаты