Уравнение Бернулли

Уравнение вида , (6)

где α - любое действительное число (α≠0,α ≠1) называется уравнением Бернулли.

Преобразование уравнения в линейное будем проводить в следующей последовательности:

1. умножим обе части уравнения на ;

2. введем подстановку , отсюдаи;

3. решаем получившееся линейное уравнение;

4. возвращаемся к искомой функции, заменяя на.

Задача №6. Найти решение задачи Коши:

6.31 .

Решение. Поделив обе части уравнения на , увидим, что это уравнение Бернулли:

.

Введем новую переменную . Тогда,или. Наше уравнение примет вид- линейное дифференциальное уравнение первого порядка. Решая его любым способом, рассмотренным в задаче №5, получимили. Тогда- общее решение исходного дифференциального уравнения.

Определим произвольную постоянную c используя начальное условие:

.

Решением задачи Коши будет являться

.

Замечание. В начале нашего решения мы обе части уравнения делили на x≠0 и могли, таким образом, потерять решение уравнения. Подставляя x=0 в исходное уравнение, убеждаемся, что оно не является его решением.

Уравнения в полных дифференциалах

Уравнение , в котором левая часть является полным дифференциалом функцииU(x,y), т.е.

(7)

(8)

называется уравнением в полных дифференциалах.

Это имеет место в том и только в том случае, когда выполняется равенство:

.

Тогда .

Интегрируем уравнение (7) по x:

(9).

Уравнение (9) продифференцируем по y:

(10).

Сравнивая (10) и(8):

.

Отсюда

.

Подставляя найденную функцию в (9) найдемU(x,y).

Задача №7. найти общий интеграл дифференциального уравнения.

.

Решение. Сгруппируем слагаемые содержащие dx и dy

.

Докажем, что это уравнение в полных дифференциалах.

Пусть , а. Т.е., необходимо показать, что.

и .

Теперь наша задача заключается в том, чтобы найти функцию U(x,y)=c, такую чтобы ее полный дифференциал был таким же, как левая часть нашего дифференциального уравнения.

Пусть (1), а(2).

Проинтегрируем уравнение (1) по переменной x, а вместо произвольной постоянной прибавим функцию, зависящую от y, т.е. (это необходимо, т.к. функцияU зависит от двух переменных, а интегрируем мы только по одной).

(3).

Продифференцируем уравнение (3) по переменной y, получим

(4).

Сравнивая уравнения (2) и (4),получим

,

.

Подставим найденную функцию φ(y) в уравнение (3):

.

Т.к., решение уравнения мы искали в виде U(x,y)=c,то ,

что и будет являться ответом.

Замечание. Уравнения в полных дифференциалах можно решать и другим способом. Заключается он в следующем. Ищут интегралы от M(x,y) и от N(x,y) по dx и dy соответственно. Затем ко всем известным членам из первого результата дописывают недостающие члены из второго, получают функцию U(x,y).

Метод изоклин

Задача№8 для данного дифференциального уравнения построить интегральную кривую, проходящую через точку М.

.

Для решения подобной задачи можно также применить метод изоклин. Изоклиной уравнения называется всякая кривая, определяемая уравнением f(x,y)=k при фиксированном k, где k=tgα=y^’.

Решение. Для приближенного (графического) решения нашего уравнения построим на плоскости изоклины для нескольких значений k. (Существование и единственность заданного дифференциального уравнения следует из того, что f(x,y)=x+2y и непрерывны всюду на плоскостиXOY).

Т.к. поле направлений исходного уравнения:

Тогда уравнения изоклин будут

.

Исследуем вид правой части заданного уравнения:

1. найдем линию экстремумов.

, отсюда .

Полученная прямая является линией экстремумов. (Непосредственной подстановкой убеждаемся, что она не является решением нашего уравнения).

когда . Значит интегральные кривые убывают до пересечения с прямой.когда. Следовательно, кривые возрастают после пересечения с прямой.

Значит, сама прямая является линией минимумов.

2. Найдем линию перегибов.

, т.е. или. Тогда. Отсюда.

Но, т.к. эта прямая является решением исходного уравнения, то она не может быть линией перегибов. А из того, что еслииеслиследует, что вогнутые интегральные кривые расположены выше этой прямой, а выпуклые – ниже.

Составим таблицу.

k	-1/2	0	1	4	5
Изоклины
		0		arctg4	arctg5

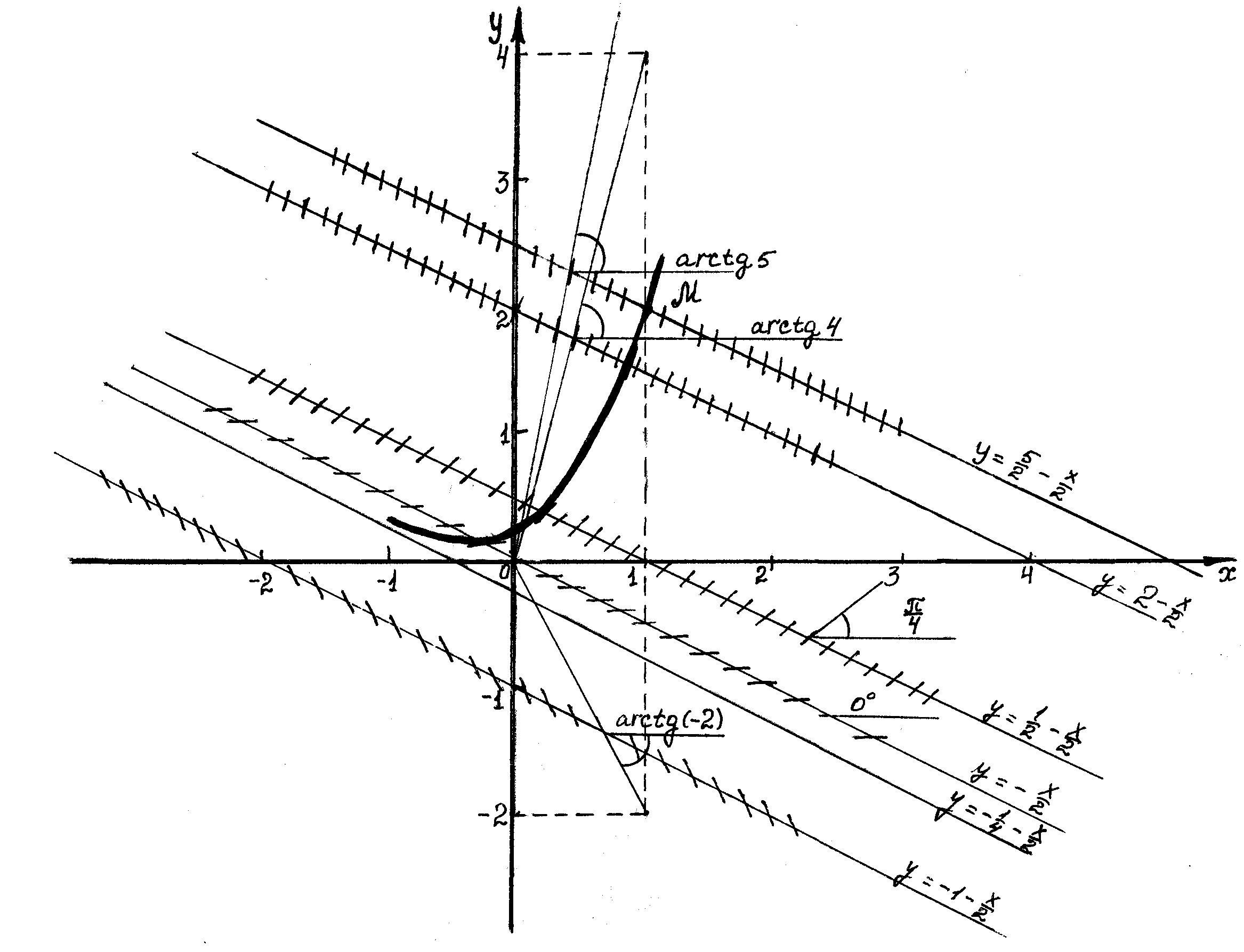
На поле направлений совпадает с самой прямой. Точка М(1,2) принадлежит изоклине . (Читателю будет полезно сравнить приближенное решение с точным, решив дифференциальное уравнение самостоятельно.)