
Лекция 1
.pdfФроленкова Лариса Юрьевна д. т. н.,
кафедра "Физика"
ауд. 324
E-mail: Larafrolenkova@yandex.ru
Литература
1.Детлаф А. А., Яворский В. М. Курс физики.
2.Яворский В. М., Детлаф А. А. Справочник по физике.
3.Савельев И. В. Курс общей физики, т. 1., т. 2, т. 3.
4.Трофимова Т. И. Курс физики.
5.Шубин А. С. Курс общей физики.
6.Волькенштейн В. С. Сборник задач по общему курсу физики.
1
Физические основы механики
Часть физики, изучающая механическое движение тел, называется механикой.
Основные законы механики установлены Галилео Галилеем (G. Galilei 1564 – 1642) и окончательно сформулированы Исааком Ньютоном (I. Newton 1643 – 1727). Механику Галилея–Ньютона называют классической механикой.
В ней изучаются законы движения макроскопических тел (это все окружающие нас тела) со скоростями, малыми по сравнению со скоростью света (с 3 108 м/с).
Более общей теорией, в которой описываются микроскопические тела (например, элементарные частицы) является, квантовая механика.
Движение макроскопических тел с любыми скоростями, в том числе и со скоростями, сравнимыми со скоростью света, рассматривает релятивистская механика, основанная на специальной теории относительности, сформулированной А. Эйнштейном (1879 – 1955).
2
Кинематика материальной точки
1.Понятие механического движения. Модель материальной точки. Система отсчета. Траектория движения.
2.Кинематические характеристики движения. Радиус-вектор, перемещение, вектор скорости, вектор ускорения.
3.Кинематические уравнения прямолинейного равномерного движения. Кинематические уравнения равноускоренного движения.
4.Движение по окружности. Связь кинематических характеристик поступательного и вращательного движений.
3
1. Понятие механического движения. Модель материальной точки. Система отсчета. Траектория движения.
Механическим движением называют изменение с течением времени положения тела в пространстве. Основными видами механического движения являются
поступательное и вращательное движения.
Поступательным движением называется движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе. При поступательном движении все точки тела движутся одинаково, поэтому можно рассматривать движение тела независимо отего размеров иформы, как движение однойточки тела.
Вращательным движением называют движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой
осью вращения.
Раздел физики, в котором механическое движение изучается без рассмотрения причин, определяющих характер движения, называется кинематикой. Основная задача кинематики – определение положения тела в пространстве и характеристик его движения в любой момент времени. Другими словами, в кинематике описывают движение,какоеоноесть,не задаваясьвопросом:"Почемудвижениеименнотакое?"
4
В физике мы имеем дело не с реальными телами, а с их физическими моделями. Простейшей моделью тела является материальная точка. Материальной точкой называется обладающее массой тело, размерами которого можно прене-
бречь в данной задаче.
Если размерами тела пренебречь нельзя, то его можно представить как совокупность материальных точек, рассматриваемых как единое целое, то есть как си-
стему материальных точек.
В процессе движения расстояние между точками, составляющими тело, может меняться – в этом случае говорят о деформации тела. Если при рассмотрении движения деформация тела незначительна (ею можно пренебречь), тогда в качестве модели тела можно использовать модель абсолютно твердого тела. Абсолютно твердым телом называется тело, расстояние между двумя любыми точками которого не изменяется.
Поступательное движение абсолютно твердого тела можно описывать как
движение одной материальной точки.
Дляописаниямеханическогодвижения(измененияположениятела) нужнопрежде всегоуметьопределятьположение тела.Дляэтойцеливводятсистемуотсчета.
5
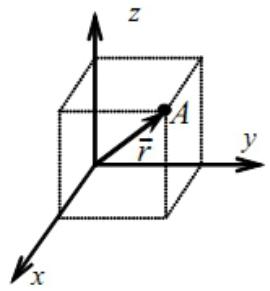
Системой отсчета называют тело отсчета, относительно которого определяется положение всех других тел, и связанные с этим телом часы. В системе отсчета обычно пользуются системой координат. Наиболее распространенной системой координат является декартова система XYZ. Для определения положения материальной точки вводится поня-
тие радиус-вектор материальной точки r – вектор, про-
веденный из начала отсчета (начала системы координат) в рассматриваемую материальную точку.
При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями
х = x (t), у = y (t), z = z (t), эквивалентными векторному уравнению r = r (t). Эти уравнения называются кинематическими уравнениями движения материальной точки.
6
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, она обладает тремя степенями свободы
(координаты х, у и z); если она движется по некоторой поверхности, то двумя степенями свободы, если вдоль некоторой линии, то одной степенью свободы.
При движении точка (конец радиус-вектора) описывает некоторую линию – траекторию движения. Траектория движения материальной точки – линия, представляющая собой совокупность точек, через которые прошла материальная точка в процессе ее движения. В зависимости от формы линии траектория может быть прямолинейной или криволинейной.
7
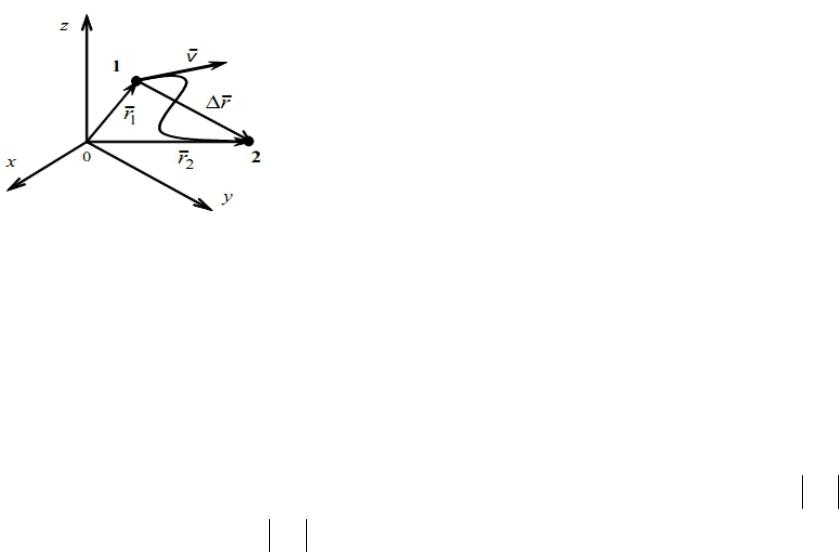
2. Кинематические характеристики движения. Радиус-вектор, перемещение, скорость, ускорение.
Для описания движения используются физические величины, которые характеризуют движение. Они называются кинематическими характеристиками.
Рассмотрим движение материальной точки вдоль произвольной траектории. Отсчет времени начнем с момента, когда точка находилась в положении 1. Длина участка траектории
12, пройденного материальной точкой с момента начала отсчета времени, называет-
ся длиной пути s и является скалярной функцией времени: s s t , м .
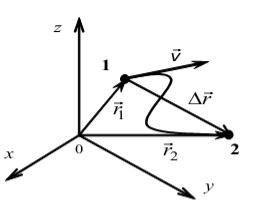
Вектор r r2 r1, проведенныйиз начального положения движущейся точки в по-
ложение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемыйпромежутоквремени),называетсяперемещением(векторнаявеличина).
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения r равен пройден-
ному пути s: s r .
8
Еслинамизвестенрадиус-вектор r материальнойточкивлюбоймоментвремени,то есть,еслимызнаемвекторную функцию r t или,чтополностью эквивалентно,триска-
лярные функции – координаты точки x t , y t , z t , мы полностью можем описать ее движение.
Однако для удобства описания движения вводят производные характеристики движения. В частности, удобно знать, как быстро радиус-вектор r t изменяется со време-
нем, то есть знать скорость движения материальной точки. Быстрота изменения любой функции,зависящейотвремени,определяетсяее производнойповремени.Вобыденной жизни под скоростью понимают путь, проходимый частицей за единицу времени. Это
есть производная пути по времени v |
ds |
, |
|
м |
. В физике чаще всего под скоростью |
|
|
||||
|
dt |
с |
|
||
понимают производную радиус-вектора r t по времени t. Поскольку радиус-вектор – этовектор,тоиегопроизводнаяявляетсявекторнойвеличиной,котораяхарактеризует не только быстроту движения частицы по траектории, но и направление, в котором движетсячастицакаждыймоментвремени.
9

Вектор мгновенной скорости (мгновенная скорость) в мо-
ментвремениtявляется,по определению производной,пределомотношения перемещения ко времени перемещения t при стремленииt к нулю, то есть отношение бесконечно малого перемещения dr к бесконечномаломувремениэтогоперемещения dt:
|
r |
|
dr |
|
|
v lim |
|
r. |
|||
|
dt |
||||
t 0 t |
|
|
|||
Вектор мгновенной скорости по определению есть перемещение в единицу времени,ионвсегданаправленпокасательнойктраектории.
Вектором средней скорости  v
v называется отношение конечного перемещения ко
называется отношение конечного перемещения ко
времениэтогоперемещения  v
v r .
r .
t
Скорость материальной точки v может изменяться со временем, как по величине, так и по направлению. Быстрота изменения вектора v – это также векторная величина, равная производной скорости v по времени, которая называется мгновенным ускоре-
|
|
|
|
|
|
|
|
м |
||
нием.Поопределениювектормгновенногоускорения a |
lim |
v |
|
dv |
v |
r, |
||||
|
|
|
|
2 |
|
|||||
|
t 0 t |
|
dt |
|
|
с |
||||
|
|
|
|
|
|
|
||||
Мгновенноеускорениеявляетсявторойпроизводнойотрадиус-вектораповремени.
Среднееускорениеявляетсяотношениемконечныхприращений  a
a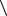 v.
v.
t
10
