2.2 Свойства сходящихся рядов

Теорема 1

Если сходится ряд, получившийся из заданного ряда отбрасыванием нескольких его членов, то сходится и сам заданный ряд. Если у сходящегося ряда отбросить несколько членов, то получится также сходящийся ряд.

Теорема 2

Если ряд сходится и его сумма равна S, то ряд , гдеc – какое-либо фиксированное число, также сходится, и его сумма равна cS.

Теорема 3

Если ряды ,

сходятся и их суммы соответственно равны S₁ и S₂ , то ряды

также сходятся, и их суммы соответственно равны и .

Итак, если ,, то.

2.3 Необходимый признак сходимости ряда

Теорема

Если ряд сходится, то предел его общего члена равен нулю при .

Этот признак не является достаточным, т.е. из того, что , еще не следует, что ряд сходится. Например, – гармонический ряд, , а ряд расходится. Но если, то ряд расходится (это следствие из теоремы), т.е. отличие от нуля является достаточным условием для расходимости ряда .

2.4 Достаточные признаки сходимости рядов с положительными членами

2.4.1 Признак сравнения

Теорема (непредельная форма признака сравнения)

Пусть даны два положительных ряда:

, ,

, .

Если члены первого ряда не больше соответствующих членов второго ряда и второй ряд сходится, то первый ряд тоже сходится.

Итак, если и, то.

Теорема

Если члены первого ряда не меньше соответствующих членов второго ряда и второй ряд расходится, то первый ряд тоже расходится.

Примечания:

1. Эти две теоремы представляют первый признак сравнения.

2. Часто оказывается полезным рассматривать не соотношение между общими членами a_n, b_n рядов, а предел их отношения при , то есть предельную форму первого признака сравнения.

Теорема (второй признак сравнения)

Если для знакоположительных рядов

,

, (4)

то эти ряды одновременно сходятся или расходятся.

Следствие. Теорема имеет место, если .

2.4.2 Признак Даламбера

Теорема (предельная форма признака)

Если для знакоположительного ряда существует

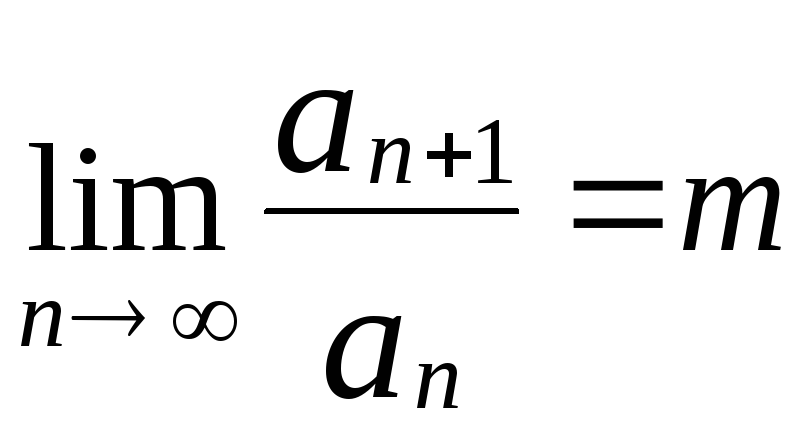, (5)

то при ряд сходится, приряд расходится; привопрос о сходимости ряда остается открытым (в этом случае необходимо применять другие признаки сходимости рядов).

2.4.3 Признак Коши

Теорема (предельная форма признака)

Если существует

, (6)

то при ряд , , сходится; при – расходится, при ряд может сходиться или расходиться (требуется дополнительное исследование).

2.4.4 Интегральный признак Коши

Теорема

Если функция непрерывная, положительная, не возрастающая для и при натуральных значениях аргумента x

, , ..., ,...,

то ряд и несобственный интегралодновременно сходятся или расходятся.

Задача 3.31 [7]

Исследовать на сходимость ряд .

Здесь, как и в других задачах типового расчета, формулой (3) не пользуются (см. примечание к задаче 2.31).

Решение:

Так как для любого n , то для .

Исследуем на сходимость ряд с общим членом . Возьмем ряд с общим членом ; – обобщенный гармонический ряд, его также называют рядом Дирихле, он сходится при и расходится при. В данном случае , т. е. расходится.

Применим второй признак сравнения. Найдем

.

Следовательно, оба ряда ведут себя одинаково в смысле сходимости.

Так как ряд Дирихле расходится, то рядтакже расходится. Возвращаясь к соотношению, по первому признаку сравнения заключаем: данный ряд расходится.

задача 4.31 [7]

Исследовать на сходимость ряд .

Решение:

Воспользуемся эквивалентным равенством: при, при . Поэтому . Значит, рассматриваем ряд. Сравним его со сходящимсярядом Дирихле. Найдемp по теореме (второй признак сравнения):

, ,

то есть ряд сходится. Следовательно, сходится и данный ряд.

Примечание. Решение задачи намного упрощается с помощью следствия второго признака сравнения (см. п. 2.4.1). Проверьте это самостоятельно.

задача 5.31 [7]

Исследовать на сходимость ряд .

Решение:

Найдем , применив признак Даламбера.

В данном случае ,

;

Таким образом, , данный ряд расходится.

задача 6.31 [7]

Исследовать на сходимость ряд .

Решение:

Здесь . Воспользуемся радикальным признаком Коши: =

.

Так как , то данный ряд сходится.

Задача 7.31 [7]

Исследовать на сходимость ряд .

Решение:

Рассмотрим вспомогательный ряд с общим членом : (знак ~ понимается как эквивалентность числовых последовательностей и при), .

Исследуем его на сходимость, пользуясь интегральным признаком Коши.

В данном случае функция удовлетворяет условиям интегрального признака при(убедитесь в этом самостоятельно).

Несобственный интеграл

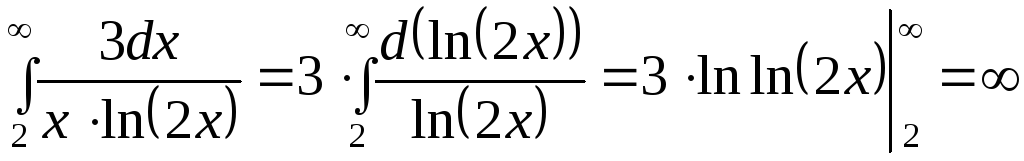, т.е. расходится, поэтому расходится и ряд. Тогда по следствию из теоремы (второй признак сравнения) заключаем, что заданный ряд тоже расходится.