
Лекции по ФХ 2 семестр / Лекция 4
.docТеории химической кинетики.
Теория активных столкновений (ТАС).
Основные предпосылки:
1. Молекулы представляют в виде шариков.
2. Для того, чтобы произошло взаимодействие, необходимо столкновение.
3. Процесс протекает только в том случае, если энергия столкновения больше или равна определенному значению энергии, которая называется энергией активации.
В основу этой теории положено два учения: молекулярно-кинетическая теория и теория Больцмана.
Вывод уравнения ТАС.
z – общее число столкновений в единицу времени.
z=![]()
Д – эффективный диаметр молекул;
n – число молекул в единице объема;
M – молекулярная масса.
С помощью закона Больцмана определяем
количество активных столкновений z![]() ,
т.е. таких, в которых энергия превышает
энергию активации:
,
т.е. таких, в которых энергия превышает
энергию активации:
z![]()
Тогда доля активных столкновений составит:
![]()
Рассмотрим бимолекулярную газовую
реакцию типа: 2А![]() ,
где Р – продукты реакции. Например, это
может быть разложение йодистого водорода:
,
где Р – продукты реакции. Например, это
может быть разложение йодистого водорода:
2HJ![]()
Теперь заметим, что в результате каждого активного столкновения расходуется две молекулы исходного вещества. Поэтому количество прореагировавших молекул в единице объема будет равна удвоенному количеству активных столкновений в то же время и в том же объеме:
![]() или
или
![]() (
(![]() )
)
Отсюда видно, что скорость реакции зависит от квадрата концентрации.
![]()
![]() =
k
=
k![]()
k=k![]() уравнение Аррениуса
уравнение Аррениуса
Сравнение этих уравнений позволяет
установить физический смысл
предэкспоненциального множителя k![]() ,
который оказывается пропорциональным
общему количеству столкновений всех
молекул в единице объема за единицу
времени.
,
который оказывается пропорциональным
общему количеству столкновений всех
молекул в единице объема за единицу
времени.
В общем виде уравнение Аррениуса для всех типов реакций часто пишут в виде:
k=z![]() уравнение Аррениуса
уравнение Аррениуса
Константа, рассчитанная по этому уравнению, не дает совпадения с экспериментальными данными. Для корректировки в это уравнение вводят стерический фактор р.
Тогда уравнение Аррениуса с точки зрения ТАС запишется следующим образом:
k = pz![]()
Считается, что стерический фактор отличается от единицы потому, что для осуществления реакции необходима определенная ориентация реагирующих молекул.
В этом уравнении Е – энергия активации, рассчитанная по ТАС, абсолютная (истинная) энергия активации, а экспериментальная – эффективная энергия активации.
Е![]()
![]()
Факты, которые не объясняет ТАС:
1. Не дает метода теоретического расчета энергии активации.
2. Не объясняет протекания в растворах.
3. Не объясняет природы стерического фактора.
МОНОМолекулярные реакции с точки зрения ТАС.
Теория Линдемана.
В элементарном акте мономолекулярной реакции участвует всего одна молекула. В соответствии с теорией активных столкновений реакция начинается со встречи двух активных молекул. Количество столкновений пропорционально квадрату концентраций. Поэтому, казалось бы, что мономолекулярные реакции, как и бимолекулярные, должны иметь порядок, равный двум. Но многие мономолекулярные реакции описываются уравнением первого порядка, причем порядок реакции может изменяться при изменении концентрации (давления) и быть дробным.
Объяснение механизмов газовых мономолекулярных реакций дано Линдеманом. Он предположил, что после столкновения активные молекулы могут не только распадаться на продукты реакции, но и дезактивироваться. Механизм реакции представляется двухстадийным:
1) A+A![]()
2)
![]()
A![]() –
активная молекула.
–
активная молекула.
На первом этапе происходит перераспределение энергии, в результате чего одна молекула становится активной, а другая дезактивируется.
На второй стадии оставшиеся активные молекулы мономолекулярно превращаются в продукты реакции.
Рассмотрим стационарный процесс:
![]()
Выразим концентрацию активной частицы
А*:
![]() .
Подставим это выражение в выражение
скорость определяющей стадии (вторая
стадия):
.
Подставим это выражение в выражение
скорость определяющей стадии (вторая
стадия):
![]() уравнение Линдемана
уравнение Линдемана
Анализ уравнения Линдемана:
1. СА – очень маленькая.
В этом случае промежутки между
столкновениями молекул настолько
велики, что дезактивация происходит
редко. Распад активных молекул на
продукты происходит без затруднений;
лимитирующей стадией является стадия
активации. В связи с этим в уравнении
Линдемана пренебрегаем в знаменателе
![]() относительно k3 (
относительно k3 (![]() <<
k3).
<<
k3).
![]() ;
n=2 (второй порядок реакции)
;
n=2 (второй порядок реакции)
2. СА – очень большая.
В этом случае лимитирующей стадией
является стадия вторая, мономолекулярная.
Затрудненность этой стадии объясняется
тем, что активные молекулы часто теряют
избыточную энергию при столкновении и
не успевают образовывать продукты
реакции. Тогда в уравнении Линдемана в
знаменателе можно пренебречь k3
относительно
![]() (
(![]() >>k3).
>>k3).
![]() ;
n=1 (реакция первого порядка)
;
n=1 (реакция первого порядка)
3. СА – средняя. В этом случае мономолекулярные реакции могут иметь дробный порядок (1<n<2).
ТЕОРИЯ АКТИВИРОВАННОГО КОМПЛЕКСА (ТАК) ИЛИ ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ (ТПС).
Основным представлением ТАК является положение о том, что всякая химическая реакция протекает через образование некоторого переходного состояния, которое затем распадается на продукты данной реакции.
Основные положения теории:
1. В ходе процесса молекулы постепенно приближаются друг к другу, в результате чего меняются межъядерные расстояния.
2. В ходе реакции образуется активированный комплекс, когда один из атомов становится как бы обобществленным, и межъядерное расстояние становится одинаковым.
3. Активированный комплекс превращается в продукты реакции.
Например, реакцию разложения йодоводорода можно представить следующим образом:
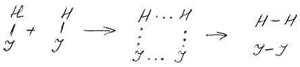
Сначала две молекулы HJ расположены достаточно далеко друг от друга. При этом существует взаимодействие лишь между атомами в молекуле. После сближения на достаточно короткое расстояние начинают возникать связи между атомами, входящими в состав разных молекул, и связи H – J становятся более слабыми. В дальнейшем они ещё более ослабевают и полностью разрываются, а новые связи H – H и J – J, наоборот, упрочняются. В результате происходит перегруппировка атомов и вместо исходных молекул НJ образуются молекулы Н2 и J2. В процессе сближения и перегруппировки атомов молекулы образуют некоторый малоустойчивый активированный комплекс из двух молекул водорода и двух молекул йода; комплекс существует очень недолго и в дальнейшем распадается на молекулы продуктов. На его образование необходима затрата энергии, равная энергии активации.
Представление об активированном комплексе и об энергии активации подтверждается с помощью энергетических диаграмм, построение которых используется в ТАК.
Активированный комплекс всегда имеет избыток энергии по сравнению с энергией реагирующих частиц.
А–В+D
![]()
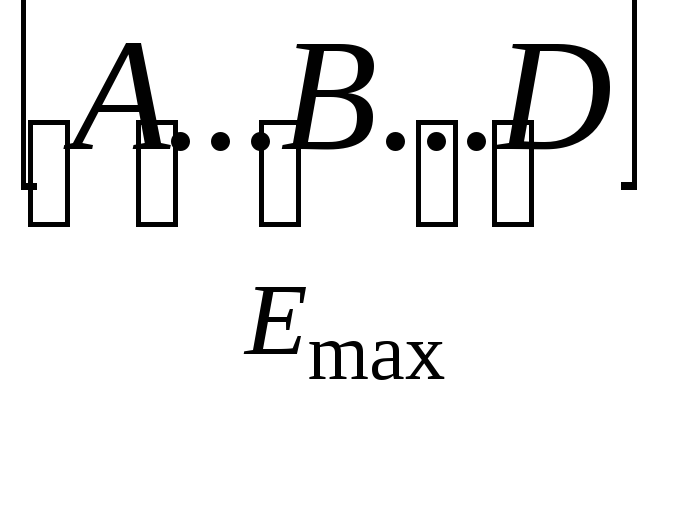 → A+B–D
→ A+B–D
переходное состояние

Е1 – энергия связи BD без А.
Е2 – энергия связи АB без D.
Е3 – энергия связи переходного состояния.
Е4 – энергия свободных атомов.
Е3 – Е2 = Е активации прямой реакции.
Е2 – Е1 = ∆Н тепловой эффект реакции.
Е4 – Е2 – энергия разрыва связи АВ.
Е4 – Е1 – энергия разрыва связи ВD.
Так как энергия разрыва связей Е4 >> Е активации, то реакция протекает с образованием активированного комплекса без предварительного разрыва связей.
Вывод основного уравнения ТАК.
Скорость процесса определяется скоростью
прохождения активированным комплексом
расстояния
![]() .
.
Обозначим:
![]() –
время жизни активированного комплекса.
–
время жизни активированного комплекса.
![]() –
концентрация активированного комплекса.
–
концентрация активированного комплекса.
![]() ,
где
,
где
![]() – средняя скорость прохождения АК через
барьер.
– средняя скорость прохождения АК через
барьер.
![]() ,
где
,
где
![]() – константа Больцмана;
– константа Больцмана;
![]() – масса комплекса; Т –
температура, К.
– масса комплекса; Т –
температура, К.
Тогда время жизни комплекса равно:
![]()
Скорость процесса:
![]() .
Подставим в это выражение значение
времени жизни комплекса
.
Подставим в это выражение значение
времени жизни комплекса
![]() :
:
![]() – скорость реакции.
– скорость реакции.
В уравнение вводится трансмиссионный
коэффициент
![]() ,
показывающий, какая доля активированных
комплексов переходит в продукты реакции.
,
показывающий, какая доля активированных
комплексов переходит в продукты реакции.
![]()
Рассмотрим бимолекулярную реакцию с позиции ТАК:
А+В
![]() АВ
АВ![]() →
АВ
→
АВ
Скорость процесса описывается кинетическим
уравнением второго порядка:
![]() .
.
Выразим константу скорости:
![]() – выражение константы равновесия.
– выражение константы равновесия.
Константу равновесия процесса образования продуктов реакции и исходных веществ можно представить следующим образом:
![]() ,
где
,
где
к* – константа равновесия процесса образования активированного комплекса;
h – постоянная Планка.
Подставим это выражение в выражение константы скорости бимолекулярной реакции:
![]() уравнение Эйринга
уравнение Эйринга
Это уравнение позволяет связать кинетические параметры с термодинамическими.
1. Вводится понятие теплоты и энтропии активации.
2. С помощью этого уравнения можно рассчитать абсолютные скорости химического процесса.
Физический смысл энтропии активации.
Энтропия активации S* – это изменение энтропии при образовании активированного комплекса.
![]()
∆S* не связана с ∆S реакции.
![]() (энтальпии активации)
(энтальпии активации)
Константа скорости реакции может быть выражена через термодинамические параметры:
![]()
![]()
![]()
![]() – подставим это выражение в уравнение
Эйринга
– подставим это выражение в уравнение
Эйринга
![]() основное уравнение ТАК
основное уравнение ТАК
Физический смысл энтальпии активации.
Прологарифмируем уравнение Эйринга:
![]()
Возьмем дифференциал по температуре Т:
![]() │
│
![]() –
уравнение Аррениуса
–
уравнение Аррениуса
![]() │
│
![]() –
уравнение изобары Вант-Гоффа
–
уравнение изобары Вант-Гоффа
![]() – связь между экспериментальной Еакт.
и энтальпией активации.
– связь между экспериментальной Еакт.
и энтальпией активации.
Так как
![]() ,
то
,
то
![]() .
.
Уравнение Аррениуса:
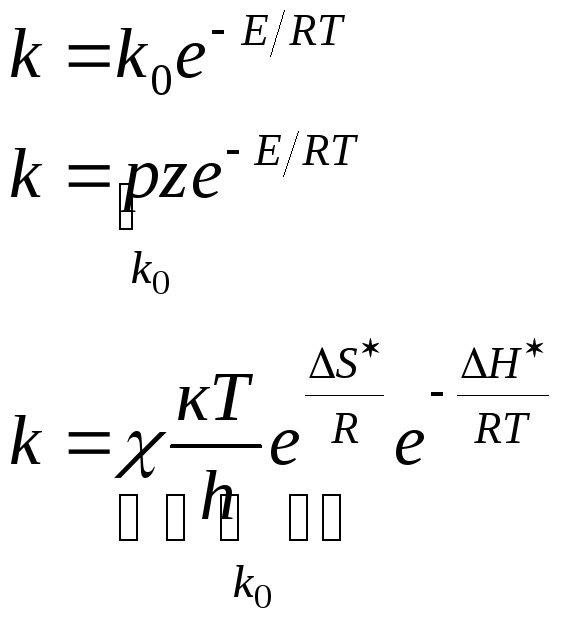
Сопоставляя эти уравнения, можно
заметить, что энтальпия активации есть
ни что иное, как энергия активации;
![]() – энтропия активации численно равна
предэкспоненциальному множителю
– энтропия активации численно равна
предэкспоненциальному множителю
![]() и произведению pz.
и произведению pz.
![]() – фактор частоты.
– фактор частоты.
![]()
ПРИМЕР. Е1 > E2;
д. б. k1 < k2; а м. б. k1 > k2 здесь играет роль энтропийный фактор
Ингибитор влияет на энтропийный фактор.
