7Б) Условия разрешимости озу на основе минимакса

Для иллюстрации смысла теоремы существования решения ОЗУ и метода ее решения на основе этой теоремы рассмотрим частный случай задачи, когда система характеризуется только двумя критериями и одним скалярным управляющим параметромu, который удовлетворяет неравенству u_1 u u₂.

Критерии не должны превосходить единицы. Область значений, при которых выполняются условиязадается неравенствами,

(12)

Выражение (12) определяет решение ОЗУ, причем все множество решений. Характерным является значение , которое соответствует, но с другой стороны, величинаравняется:

(13)

Сначала фиксируем значение u и находим наибольшее из двух величин и. Оно равняется, если, и, если. Далее минимизируем эту величину поu, и найдем при. Если=1, то существует решение ОЗУ, причем единственное, равное. Если<1, то решение ОЗУ существует и оно не однозначное. При>1 решения ОЗУ не существует. В этом случае синтез системы невозможен.

Полученное условие существования решения ОЗУ <1 можно использовать для поиска решения ОЗУ. Например, зададимся каким-либо значением управленияu=u⁽¹⁾ из отрезка [u₁, u₂]. Вычисляем и. Еслии, то найдено одно решениеu=u⁽¹⁾. Если же хотя бы одно из них больше единицы, то u⁽¹⁾ не является решением ОЗУ. Для нахождения следующего приближения определим Г=max[,]. Пусть Г=. Следующее приближение u⁽²⁾=u⁽¹⁾+u⁽¹⁾ определим из условия уменьшения , например, используя метод градиентного спуска, т. е.

Задаваясь малым параметром , характеризующим шаг приближения, согласно методу градиентного спуска, получим:

.

Теперь вычислим ипри управлениии сравниваемс единицей. Если обаменьше единицы, тоu⁽²⁾ одно из решений ОЗУ. В противном случае находим max[] и производим следующий шаг градиентного спуска. Этот процесс продолжается до тех пор, пока не получим или же не найдемили не убедимся, что, т. е. решения ОЗУ не существует.

Но если функция имеет несколько максимумов, то метод градиентного спуска, вообще говоря, гарантирует нахождение только относительного минимума. Для утверждения того, что ОЗУ не имеет решения, следует найти абсолютный минимум выражения

Условие

(14)

при выполнении связей (2) является необходимым и достаточным условием существования решения ОЗУ.

Достаточность. Допустим, что существует решение системы (11) удовлетворяющее условию (14). Используя (2) для каждого управления вычислими найдем

Необходимость. Допустим, что условие (14) нарушается, т. е. Г_о>1. Но исовпадает с одним из значений какого либо из функционалов, например.

12-13) Оптимизация многостадийных (многошаговых) процессов. Принцип оптимальности. Уравнение Беллмана

Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги).

Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.

Экономический процесс является управляемым, если можно влиять на ход его развития.

Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.

Операция – управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.

Решение на каждом шаге называется «шаговым управлением».

Совокупность всех шаговых управлений представляет собой управление операцией в целом.

При распределении средств между предприятиями шагами целесообразно считать номер очередного предприятия; при распределении на несколько лет ресурсов деятельности предприятия – временной период. В других задачах разделение на шаги вводится искусственно.

Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:

F(x)=

Где F – выигрыш за операцию;

F_i(x_i) – выигрыш на i-м шаге;

х – управление операцией в целом;

х_i – управление на i-м шаге (i=1,2,…,m). В общем случае шаговые управления (х₁, х₂, … х_m) могут стать числами, векторами, функциями.

То управление (х*), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управлений х* = х*₁, х*₂, … х*_m

F* = max {F*(х*)} – максимальный выигрыш, который достигается при оптимальном управлении х*.

Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений

Принцип оптимальности Беллмана.

Основным методом динамического программирования является метод рекуррентных соотношений; который основывается на использовании принципа оптимальности, разработанного американским математиком Р.Беллманом.

Суть принципа:

Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться ОПТИМАЛЬНЫМИ относительно состояния, к которому придет система в конце каждого шага.

Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.

Условная оптимизация

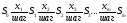
Безусловная оптимизация

S_i – состояние системы на i-м шаге. Основная рекуррентная формула динамического программирования в случае решения задачи максимизации имеет вид:

, где максимум в данной формуле берется по всем возможным решениям в ситуации, когда система на шаге m находится в состоянии i.

Величина f_m(i) – есть максимальная прибыль завершения задачи из состояния i, если предположить, что на шаге m, система находится в состоянии i.

Максимальная прибыль может быть получена максимизацией суммы прибылей самого шага m и максимальной прибыли шага (m+1) и далее, чтобы дойти до конца задачи.

Планируя многошаговую операцию надо выбирать управление на каждом шаге с учетом всех его будущих последствий на ещё предстоящих шагах.

Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимальным, а так, чтобы была максимальна сумма выигрышей на всех оставшихся шагах плюс данный шаг.

Среди всех шагов последний шаг планируется без оглядки на будущее, т.е. чтобы он сам, как таковой принес наибольшую выгоду.

Задача динамического программирования начинает решаться с конца, т.е. с последнего шага. Решается задача в 2 этапа:

1 этап (от конца к началу по шагам): Проводится условная оптимизация, в результате чего находится условные оптимальные управления и условные оптимальные выигрыши по всем шагам процесса.

2 этап (от начала к концу по шагам): Выбираются (прочитываются) уже готовые рекомендации от 1-го шага до последнего и находится безусловное оптимальное управление х*, равный х*₁, х*₂, …, х*_m.

11абв)Постановка задачи оптимизации. Понятие оптимизации. Примеры

Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях

При постановка задачи предполагается существование конкурирующих свойств того или иного технологического процесса, например: 1) количество продукции - расход сырья" ; 2)количество продукции - качество продукции"

Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.

При постановке задачи оптимизации необходимо:

1. Наличие объекта оптимизации и цели оптимизации.

Типичный пример неправильной постановки задачи оптимизации: "Получить максимальную производительность при минимальной себестоимости".

Ошибка заключается в том, что ставится задача поиска оптимума 2-х величин, противоречащих друг другу по своей сути.

2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы - управляющими воздействиями. 

3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.

4. Учет ограничений.

ИЛИ

• установление границы подлежащей оптимизации системы, т.е. представление системы в виде некоторой изолированной части реального мира.

• определение показателя эффективности, на основе которого можно оценить характеристики системы или ее проекта с тем, чтобы выявить "наилучший" проект или множество "наилучших" условий функционирования системы. "Наилучшему" варианту всегда соответствует экстремальное значение показателя эффективности функционирования системы;

• выбор внутрисистемных независимых переменных, которые должны адекватно описывать допустимые проекты или условия функционирования системы и способствовать тому, чтобы все важнейшие технико-экономические решения нашли отражение в формулировке задачи;

• построение модели, которая описывает взаимосвязи между переменными задачи и отражает влияние независимых переменных на значение показателя эффективности.

Критерием оптимальности называется количественная оценка оптимизируемого качества объекта. На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации. Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.

Все оптимизационные задачи имеют общую структуру. Их можно классифицировать как задачи минимизации(максимизации) M-векторного векторного показателя эффективности W_m(x), m=1,2,...,M, N-мерного векторного аргумента x=(x₁,x₂,...,x_N), компоненты которого удовлетворяют системе ограничений-равенств h_k(x)=0, k=1,2...K, ограничений-неравенств g_j(x)>0, j=1,2,...J, областным ограничениям x_li<x_i<x_ui, i=1,2...N.

Все задачи принятия оптимальных решений можно классифицировать в соответствии с видом функций и размерностью W_m(x), h_k(x), g_j(x) и размерностью и содержанием вектора x:

• одноцелевое принятие решений - W_m(x) - скаляр;

• многоцелевое принятие решений - W_m(x) - вектор;

• принятие решений в условиях определенности - исходные данные - детерминированные;

• принятие решений в условиях неопределенности - исходные данные - случайные.