Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Нижегородский государственный

технический университет им. Р.Е. Алексеева

Кафедра «Ядерные реакторы и энергетические установки»

Объединение и сравнение экспериментальных данных

Методические указания к лабораторным работам по дисциплине

«Методы научных исследований»

для студентов специальности

070500 «Ядерные реакторы и энергетические установки»

дневной формы обучения

Лабораторная работа №2

Нижний Новгород - 2008

Составитель В.В. Иванов

УДК 621.039

Объединение и сравнение экспериментальных данных: метод. указания к лаб. работе по дисциплине: «Методы научных исследований» для студентов специальности 070500 «Ядерные реакторы и энергетические установки» дневной формы обучения /НГТУ; сост.: В.В. Иванов. Н.Новгород, 2008 – 8с.

Редактор Э.Б. Абросимова

Подп. в печ. 7.06.08. Формат 60x841/16. Бумага газетная. Печать офсетная. Печ. л. 0,5. Уч.-изд. л. 0,2. Тираж 100 экз. Заказ .

Нижегородский государственный технический университет.

Типография НГТУ. 603950, г. Н.Новгород, ул. Минина, 24.

© Нижегородский

государственный

технический

университет, 2008

1. Цель работы

Освоение методов объединения и сравнения экспериментальных данных:

• проведение оценки воспроизводимости серии экспериментов по критерию Кохрена;

• выбор наилучшей серии экспериментов;

• объединение результатов нескольких серий эксперимента по методу взвешенного среднего.

2. Основы теории

1. Критерии воспроизводимости серии экспериментов

Ответственные эксперименты должны быть проверены на вос-производимость результатов, т.е. на их повторяемость в определенных пределах измерений с заданной доверительной вероятностью. Суть такой проверки сводится к следующему. Имеется несколько параллельных опытов (серий). Для каждой серии вычисляют среднеарифметическое значение . Далее вычисляют дисперсию. Для большой выборки и нормального закона распределения дисперсияявляется общей оценочной характеристикой:

. (1)

Дисперсия характеризует однородность измерения. Чем выше , тем больше разброс измерений.

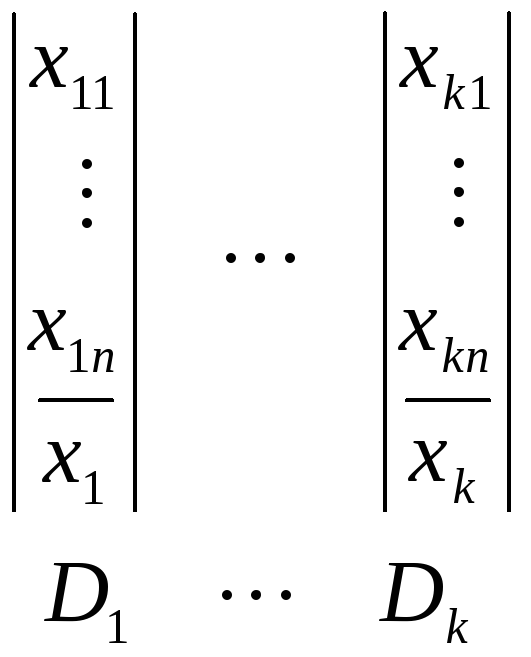
Чтобы оценить воспроизводимость, оценивают критерий Кохрена (расчетный):

, (2)

где maxD и ‑ наибольшее значение дисперсий из числа рас-сматриваемых параллельных серийmи сумма дисперсийmсерий.

Рекомендуется принимать (у нас в работеm=4).

Опыты считаются воспроизводимыми при , где- табличное значение критерия Кохрена (см. Приложение), принимаемое в зависимости от доверительной вероятности, числа степеней свободы(n– число измерений в серии) и количества серий эксперимента.

2. Объединение и сравнение данных в результате эксперимента. Взвешенные средние Проблема объединения результатов разных измерений

Два студента А и Б тщательно измеряют величину х и получают следующие результаты:

студент А: x = x_А_А студент Б: x = x_Б_Б.

x_А может быть средним всех измерений студента А и _А– среднеквадратичное отклонение измеряемой величины (аналогично для x_Б и _Б). Вопрос теперь состоит в том, как лучше всего объединить x_А и x_Б, чтобы получить единственную наилучшую оценку для x: x_А – x_Б  _А и _Б.

Если различия x_А – x_Б между двумя измерениями намного больше обеих погрешностей _А и _Б, то, по–видимому, что-то не в порядке по крайней мере в случае одного из измерений. Два измерения противоречивы, и необходимо тщательно проанализировать оба измерения.

Предположим, что два измерения непротиворечивы, т.е. различие x_А – x_Б не намного больше, чем любая из погрешностей _А и _Б. Какова наилучшая оценка x_наил истинного значения х. Первой реакцией могло быть вычисление среднего значения (x_А + x_Б)/2 двух измерений. Этот путь не подходит, если две погрешности _А и _Б не равны. Вычисление простого среднего делает одинаково важными оба измерения, в то время как более точному отсчёту следует приписать больший вес.