Нижегородский Государственный Технический Университет

Выксунский филиал

Лабораторная работа по физике № 1-3

"Определение момента инерции методом трифилярного подвеса".

Выполнила: Герасимова Е. Н.

Группа ПТК – 09

Проверил: Маслов В. П.

г. Выкса 2009 год

Трифилярный подвес

1. Актуальность работы. В природе и технике весьма распространенным является вращательное движение, которое описывается в физике основным законом динамики вращательного движения. Этот закон в случае неподвижной оси вращения можно рассматривать как аналог II закона Ньютона, в котором роль меры инертности играет момент инерции абсолютно твердого тела. Расчет момента инерции твердого тела относительно произвольной оси является в общем случае сложной математической задачей. Для решения этой задачи часто удобнее использовать экспериментальные методы.

2. Цель работы. Экспериментальное определение момента инерции диска, цилиндра, и параллелепипеда относительно главных осей инерции этих твердых тел; исследование зависимости момента инерции от распределения массы тела относительно оси вращения; экспериментальная проверка теоремы Штейнера.

3. Практическая ценность. В работе изучается используемый в практике метод измерения момента инерции твердых тел. В процессе работы студенты получают навыки измерения момента инерции твердых тел методом крутильных колебаний трифилярного подвеса и умение рассчитывать момент инерции относительно осей симметрии тела.

4. Краткие сведения из теории.

1

Δm_i

r_i

) Рассмотрим твердое тело, которое может вращаться около оси ОО₁. Разобьем его на большое число (n) малых объемов ΔV_i с массами Δm_i и будем рассматривать каждый такой элемент в виде материальной точки. Через r_i обозначим соответствующее расстояние от материальной точки до оси ОО₁ (рис. 1). Величина Δm_ir_i² называется моментом инерции данной материальной точки относительно оси вращения ОО₁. Момент инерции всего тела относительно ОО₁ будет равен сумме моментов инерции всех материальных точек, на которые мы разбили твердое тело:

.

Следует заметить, что величина момента инерции твердого тела зависит не только от величины массы тела, но также от распределения массы тела относительно оси вращения. Если вещество в теле распределено непрерывно, то сумма заменяется интегралом и момент инерции тела относительно оси ОО₁ запишется:

, (1)

где r – расстояние от элементарной массы dm до оси вращения.

Если известен момент инерции тела относительно оси, проходящей через его центр масс J_c, то момент инерции относительно любой другой параллельной оси определяется теоремой Гюйгенса-Штейнера:

, (2)

где J_c – момент инерции тела относительно оси, проходящей через центр масс; m – масса тела; a – расстояние между осями.

Вычислние момента инерции тела относительно оси часто можно упростить, вычислив предварительно вспомогательную величину – момент инерции тела относительно точки. Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых состоит тело, на квадрат их расстояний R до этой точки О: .

В случае непрерывного распределения масс эта сумма сводится к интегралу:

.

Если в качестве точки О выбрать точку, в которой пересекаются три взаимно перпендикулярные оси, например X, Y, и Z, то справедливо следующее соотношение (приводим без доказательства):

, (3)

т.е. сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.

Другое следствие можно получить для плоского распределения масс. Пусть имеется бесконечно тонкая пластинка произвольной формы. Можно считать, что вещество распределено бесконечно тонким слоем по математической плоскости XOY. При этом будет справедливо соотношение

(4)

(оси x, y, z пересекаются в точке О, ось Z перпендикулярна плоскости xoy).

2) Крутильные колебания твердого тела являются частным случаем вращательного движения. Гармонические крутильные колебания могут совершать твердые тела, подвешенные на упругой нити. Если тело, например, круглый диск (рис. 2), подвесить на проволоке так, чтобы линия подвеса проходила через центр тяжести диска, и, закрутив его на некоторый угол α, отпустить, то диск будет совершать крутильные колебания.

Уравнение движения диска

,

где - момент упругих сил, действующих со стороны проволоки. При небольших деформациях (углах закручивания) момент упругих сил пропорционален величине деформации:

,

г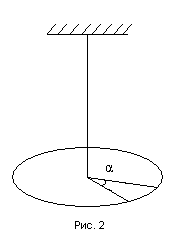де k – коэффициент пропорциональности, зависящий от упругих свойств материала проволоки; α – угол закручивания проволоки. В этом случае

.

Так как ,

то .

Это уравнение описывает крутильные гармонические колебания вида

,

где называется угловой или циклической частотой колебания. Период таких колебаний

,

т. е. зависит от момента инерции относительно оси, вокруг которой происходят колебания. Отсюда, зная упругость нити и измерив период крутильных колебаний, можно определить момент инерции диска.

5. Экспериментальная часть

Платформа в нерабочем положении арретирована, т. е. покоится на столике, который можно опускать и поднимать, закрепляя на нужной высоте с помощью специального винта на штативе. Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота треноги вокруг ее оси с помощью шнура, приводящего в движение рычажок, связанный с треногой. Этим достигается почти полное отсутствие других, некрутильных колебаний, затрудняющих измерения.

Высоту «h» подъема платформы определяем с помощью индикатора с точностью до 1,0·10^-2 мм (рис. 4).

Задания для студентов, выполняющих работу:

• Определить момент инерции нагруженной платформы;

• Определить моменты инерции конкретных тел опытным путем;

• Определить моменты инерции конкретных тел теоретическим путем.

6. Расчеты

6.1

Определение моментов инерции

тел опытным путем

И

h- высота, за время полных колебаний

h_{платформы}=0,0035м

h_{парллепипеда}=0,0027м

h_диска=0,0018м

h_{цилиндра}=0,001м

меем:

m_{платформы} =(0,415±0,001)кг

m_{параллелепипеда} = (0,419±0,001)кг

m_диска(1,103±0,001)кг

m_{цилиндра}(1,106±0,001)кг

Экспериментально измерено:

N=3 – количество измерений для каждого тела;

n=30 – количество полных колебаний.

Таблица 1

Тело	t1,с	t2,с	t3,с
Пустая платформа	202	203	204
Диск	126	128	127
Цилиндр	127	126	126
Параллелепипед («лежа»)	148	147	149
Параллелепипед («стоя»)	143	144	143
Параллелепипед («на боку»)	143	145	142

Усредняем результат измерения по формуле:

, с.

Определим средний период колебаний:

, с.

• Пустая платформа:

;

• Диск:

;

• Цилиндр:

;

• Параллелепипед («лежа»):

;

• Параллелепипед («стоя»):

;

• Параллелепипед («на боку»):

;

Результаты расчетов сведем в таблицу:

Таблица 2

Тело	<t>,с	<T>,с
Пустая платформа	217	6,7
Диск	127	4,2
Цилиндр	126,3	4,2
Параллелепипед («лежа»)	148	4,9
Параллелепипед («стоя»)	143,3	4,8
Параллелепипед («на боку»)	143,3	4,8

6.2

Рассчитаем момент инерции

1. Пустой платформы:

, кг·м²

где h=0,0026 м – высота подъема платформы при повороте на угол a₀, определяем с помощью индикатора с точностью до 1,0·10^-2мм.

g=9,81м/с² ‑ ускорение свободного падения

π=3, 14

a₀=π/2 – угол поворота платформы (в радианах)

m=0,415 кг – масса платформы

2. Нагруженной платформы Jсист по формуле:

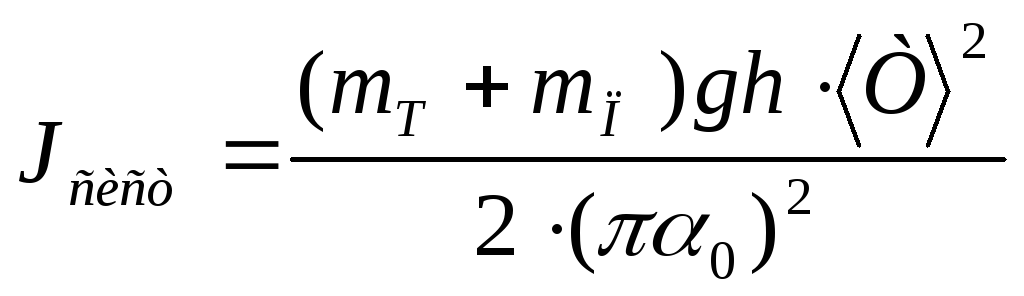, кг·м²

3. Диска, цилиндра и параллелепипеда по формуле:

, кг·м²

Диск

Цилиндр

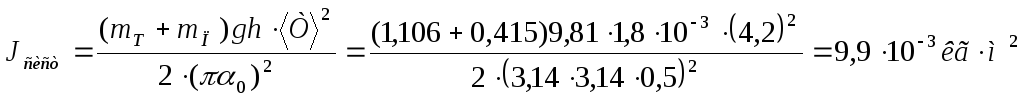
Параллелепипед («лежа»)

Параллелепипед («стоя»)

Параллелепипед («на боку»)

Результаты расчетов сведем в таблицу:

Таблица 3

Тело	Jтела·10-3 ,кг·м²	Jсист·10-3 , кг·м²
Пустая платформа	9,5
Диск	0,3	9,8
Цилиндр	0,4	9,9
Параллелепипед («лежа»)	1,5	11,04
Параллелепипед («стоя»)	0,5	10,02
Параллелепипед («на боку»)	0,5	10,02

6.3

Статистическая обработка результатов

прямых измерений.

Определяем абсолютную погрешность измерения времени:

где t =4,3 – соответствующий коэффициент Стьюдента;

при N=3 (доверительная вероятность 95%);

где S_t – среднеквадратичное отклонение.

Определяем относительную погрешность ε_t измерения времени для каждого тела:

Пустая платформа

Диск

Цилиндр

Параллелепипед («лежа»)

П араллелепипед («стоя»)

П араллелепипед («на боку»)

Результаты расчетов сведем в таблицу:

Тело	St	∆t, с	εt, %
Пустая платформа	0,58	2,5	1,2
Диск	0,58	2,5	1,9
Цилиндр	0,33	1,4	1,12
Параллелепипед («лежа»)	0,58	2,5	1,7
Параллелепипед («стоя»)	0,33	1,4	0,98
Параллелепипед («на боку»)	0,88	3,8	2,6

Таблица 4

6.4

Статистическая обработка результатов косвенных измерений.

1. Определяем относительную погрешность ε_T измерения периода колебаний:

где ε_n – относительная погрешность измерения числа полных колебаний n

2. Определяем абсолютную погрешность ∆T измерения периода колебаний:

, с

Пустая платформа :

;

с;

Диск:

с;

Цилиндр:

с;

Параллелепипед («лежа»):

с;

Параллелепипед («стоя»):

с;

Параллелепипед («на боку»):

3. Определяем относительную и абсолютную погрешности полученного экспериментального момента инерции платформы:

, кг·м²

∆J₀=0,0095·3,2=0,03 кг·м²;

4. Аналогично определяем относительную и абсолютную погрешности момента инерции системы (платформы с телом).

,кг·м²

Диск

< h>=0,0018 м

Цилиндр

<h>=0,0018

Параллелепипед («лежа»)

< h>=0,0027

Параллелепипед («стоя»)

<h>=0,0027

Параллелепипед («на боку»)

<h>=0,0027

5. Определяем относительную и абсолютную погрешности момента инерции тела.

, кг·м²

Диск

кг·м²

Цилиндр

кг·м²

Параллелепипед («лежа»)

кг·м²

Параллелепипед («стоя»)

кг·м²

Параллелепипед («на боку»)

кг·м²

Полученные результаты статистической обработки косвенных измерений занесем в таблицу:

Таблица 5

Тело	εJсист	∆Jсист	∆Jт кг·м²	εJт	εT, %	∆T,с	εJ0	∆J0, кг·м²
Пустая платформа					1,9	0,13	3,2	0,03
Диск	3,2	0,312	3,2	326,5	2,4	0,103
Кольцо	3,2	0,312	3,2	323,2	1,9	0,08
Параллелепипед («лежа»)	3,15	0,347	3,15	285,3	2,3	0,12
Параллелепипед («стоя»)	3,15	0,316	3,15	314,4	1,8	0,09
Параллелепипед («на боку»)	3,15	0,316	3,15	314,4	3	0,14