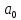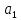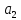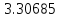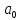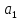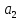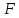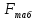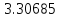- •Курсовая работа
- •Математическое моделирование энергетических состояний мозга в условиях нарушения кислородного режима
- •2014 Содержание
- •1. Введение
- •2. Постановка задачи
- •2.1. Биологическая формулировка задачи исследования
- •2.2. Математическая формулировка задачи исследования
- •3.1. Первый этап решения математической задачи
- •3.1.1. Исходные данные
- •Обработанные таблицы
- •3.1.2. Обработка экспериментальных данных
- •3.2. Подбор кривой
- •3.2.1. Формирование вариационных рядов экспериментальных данных
- •3.2.2. Выбор аппроксимирующей функции
- •3.2.3. Оценка значимости выбора функции как аппроксимирующей количественную зависимость между митохондриальной креатинкиназы (ми кк(х)) и цитоплазматической креатинкиназы (цит кк(y))
- •3.2.4. Блок-схема алгоритма решения первого этапа математической задачи
- •3.2.5. Результат решения первого этапа математической задачи
- •3.2.6. Геометрическая интерпретация количественной зависимости между показателями митохондриальной креатинкиназы (ми кк(х)) и цитоплазматической креатинкиназы (цит кк(y))
- •3.2.7. Значение параметров функции в каждом рассматриваемом эксперименте
- •3.3. Второй этап решения математической задачи
- •3.3.1. Формулировка математической задачи
- •3.3.2. Решение задачи
- •3.3.3. Геометрическая интерпретация зависимостей
- •3.3.4. Результаты определения параметров функции
- •3.4. Проверка прогностической способности модели
- •4. Заключение
3.2.3. Оценка значимости выбора функции как аппроксимирующей количественную зависимость между митохондриальной креатинкиназы (ми кк(х)) и цитоплазматической креатинкиназы (цит кк(y))
Оценкой значимости уравнения регрессии является коэффициент детерминации:
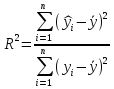 , (9)
, (9)
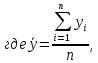
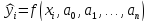 ,
,
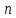 -
число экспериментов
-
число экспериментов
Вероятностная значимость коэффициента
детерминации
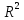 определяется по
определяется по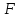 критерию Фишера-Снедекора, определенная
на уровне значимости
критерию Фишера-Снедекора, определенная
на уровне значимости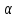 при
при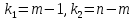 -степенях
свободы:
-степенях
свободы:
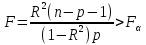 (10)
(10)
где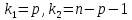 ;
;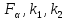 -
находятся по таблице.
-
находятся по таблице.
Для нашего случая
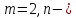 число
экспериментов.
число
экспериментов.
3.2.4. Блок-схема алгоритма решения первого этапа математической задачи
3.2.5. Результат решения первого этапа математической задачи
Расчет параметров
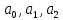 произведен
произведен
Результат работы программы приведен в Таблице 20.
|
Условие эксперимента |
|
|
|
|
Ишемия 30 минут (0,5 часа) |
|
|
|
|
Ишемия 18 часов |
|
|
|
|
Ишемия 3 дня (72 часа) |
|
|
|
|
Ишемия 7 дней (168 часов) |
|
|
|
|
Ишемия 30 дней (720 часов) |
|
|
|
|
Интактные животные |
|
|
|
Таблица 10. Расчет параметров апроксимирующей функции
30 минут
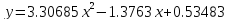
18 часов
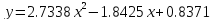
3 дня
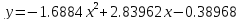
7 дней
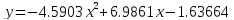
30 дней
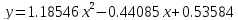
Интактные
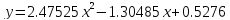
3.2.6. Геометрическая интерпретация количественной зависимости между показателями митохондриальной креатинкиназы (ми кк(х)) и цитоплазматической креатинкиназы (цит кк(y))
Покажем наглядно количественную зависимость между показателями митохондриальной креатинкиназы (ми КК(х)) и цитоплазматической креатинкиназы (цит КК(y)). Результаты представлены на рисунках 1-6.
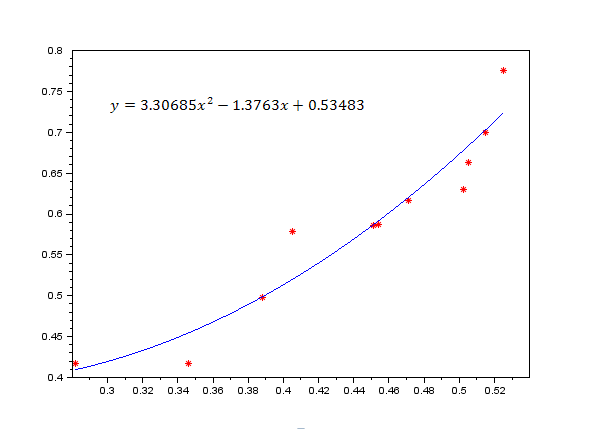
Рисунок 1. 30 минут
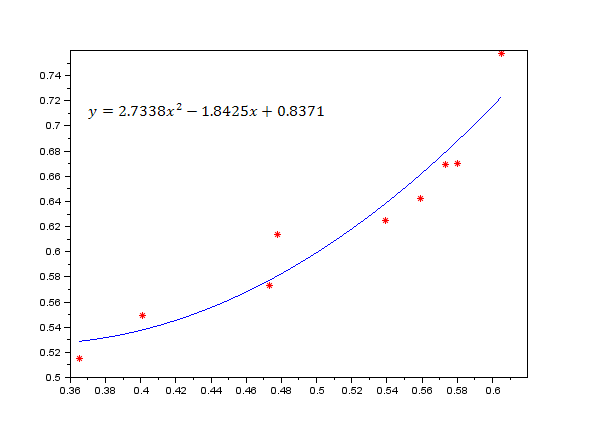
Рисунок 2. 18 часов
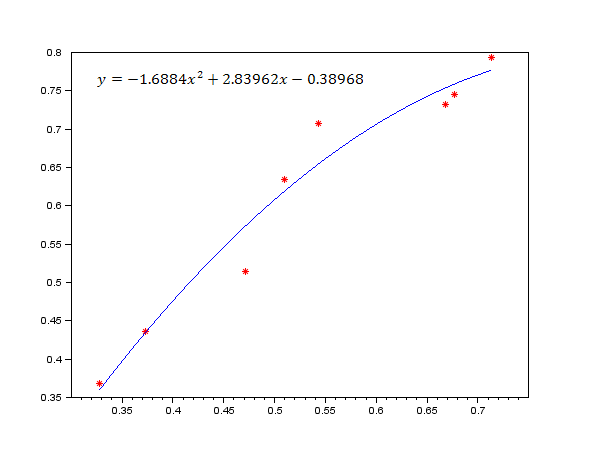
Рисунок 3. 3 дня
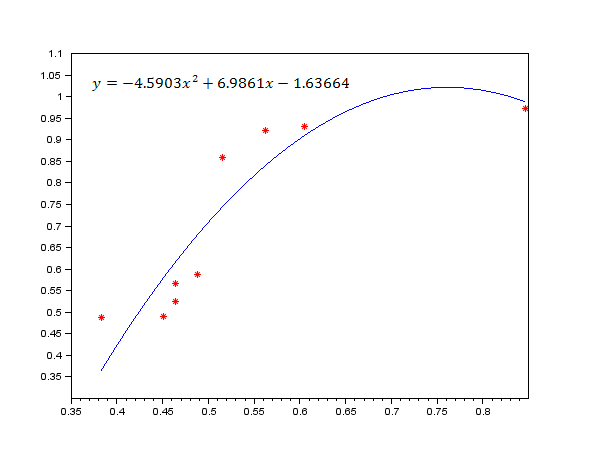
Рисунок 4. 7 дней
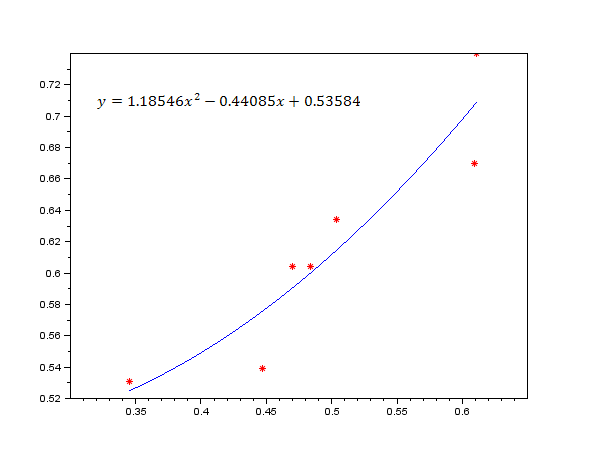
Рисунок 5. 30 дней
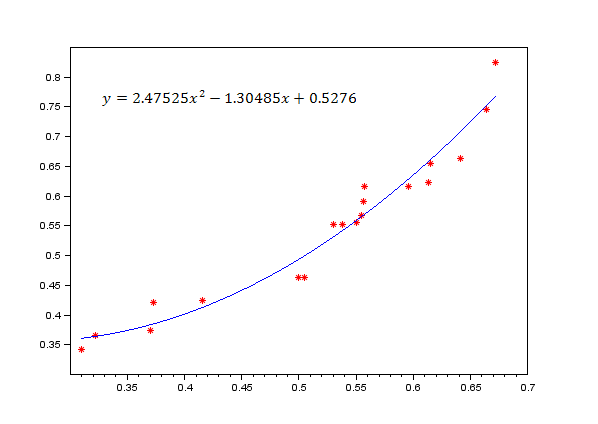
Рисунок 6. интактные животные
3.2.7. Значение параметров функции в каждом рассматриваемом эксперименте
|
Условие эксперимента |
|
|
|
|
|
|
|
Ишемия 30 минут (0,5 часа) |
|
|
|
|
|
|
|
Ишемия 18 часов |
|
|
|
|
|
|
|
Ишемия 3 дня (72 часа) |
|
|
|
|
|
|
|
Ишемия 7 дней (168 часов) |
|
|
|
|
|
|
|
Ишемия 30 дней (720 часов) |
|
|
|
|
|
|
|
Интактные животные |
|
|
|
|
|
|
Таблица 11. Расчет коэффициентов апроксимирующей функции, коэффициента детерминации и вероятной значимости.
Коэффициент детерминации
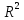 близок к 1, что свидетельствует о тесном
примыкание наблюдений к линии регрессии.
Следовательно, регрессионная модель
хорошо аппроксимирует эмпирические
данные показателей митохондриальной
креатинкиназы (ми КК(х)) и цитоплазматической
креатинкиназы (цит КК(y))
в условиях интактного состояния и в
условиях ишемического воздействия
разной продолжительности.
близок к 1, что свидетельствует о тесном
примыкание наблюдений к линии регрессии.
Следовательно, регрессионная модель
хорошо аппроксимирует эмпирические
данные показателей митохондриальной
креатинкиназы (ми КК(х)) и цитоплазматической
креатинкиназы (цит КК(y))
в условиях интактного состояния и в
условиях ишемического воздействия
разной продолжительности.
Вероятностная значимость коэффициента
детерминации
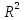 определяется по
определяется по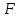 критерию Фишера-Снедекора, определенная
на уровне значимости
критерию Фишера-Снедекора, определенная
на уровне значимости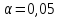 при
при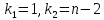 -степенях
свободы. Во всех рассматриваемых случаях
наблюдается
-степенях
свободы. Во всех рассматриваемых случаях
наблюдается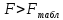 .
.
3.3. Второй этап решения математической задачи
3.3.1. Формулировка математической задачи
Даны коэффициенты
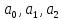 функции
функции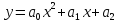 ,
зависящие отt,
характеризующей длительность нарушения
гемодинамики мозга (экспозиции
ишемического воздействия), т.е
,
зависящие отt,
характеризующей длительность нарушения
гемодинамики мозга (экспозиции
ишемического воздействия), т.е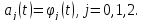
Требуется подобрать вид зависимостей
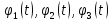 и функцию
и функцию
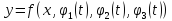 ,
характеризующую энергетическое состояние
мозга при ишемии разной продолжительности.
,
характеризующую энергетическое состояние
мозга при ишемии разной продолжительности.