
- •Введение.
- •Постановка начальной задачи.
- •Применение метода дополнительного аргумента к решению характеристической системы.
- •Доказательство эквивалентности систем (8) и (26).
- •Доказательство существования решения задачи Коши
- •Постановка задачи численного расчёта.
- •Дискретизация исходной задачи и её решение итерациями.
- •Программа и её описание. Результаты вычислений.
- •Заключение.
- •Литература
- •Оглавление
Постановка задачи численного расчёта.
Для решения исходной задачи воспользуемся системой (26) и, для удобства, третьим уравнением
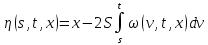
Решение будем рассматривать в области

Рассмотрим несколько
примеров с конкретными значениями
параметров и заданной функцией
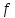 .
.
Пример 1. В качестве
функции
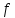 выберем
выберем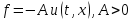 .
Тогда исходное уравнение примет вид:
.
Тогда исходное уравнение примет вид:
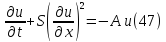
В качестве начального условия возьмём функцию
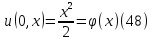
Дифференцируя (47)
по
 и полагая
и полагая ,
,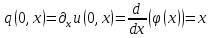 ,
получаем следующее уравнение:
,
получаем следующее уравнение:
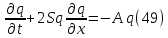
Используя метод характеристик, получаем:
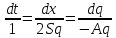
А значит,
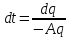
Следовательно,
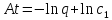 ,
,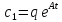 .
.
Из равенства
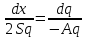
cледует
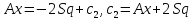 .
.
При
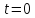
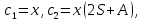 а значит,
а значит,
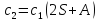
То есть
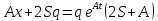
Выразив
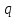 ,
получаем:
,
получаем:
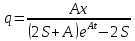
Как
видно, решение получилось глобальное,
т.е.
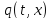 определена для любого
определена для любого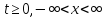 .
.
Интегрируя, получаем
решение исходной задачи – функцию
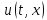 :
:
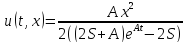
Очевидно,
что чем больше значение
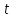 ,
тем ближе значения функции
,
тем ближе значения функции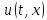 к нулю. Также можно заметить, что график
функции будет симметричен относительно
плоскости
к нулю. Также можно заметить, что график
функции будет симметричен относительно
плоскости или
или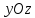 .
.
Теперь найдём решение исходного уравнения с помощью метода дополнительного аргумента.
Имеем:
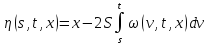
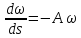
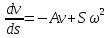
Второе
уравнение можно рассматривать как
обыкновенное дифференциальное уравнение
с разделяющимися переменными относительно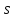 .
Тогда
.
Тогда
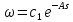
Подставляя
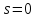 ,
получаем
,
получаем
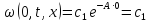
Вспоминая,
что
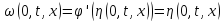 получаем:
получаем:
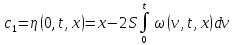
Т.е.
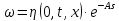
Третье
уравнение можно рассматривать как
линейное неоднородное дифференциальное
уравнение относительно переменной .
.
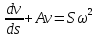
Помножим обе части уравнения на
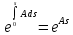
Тогда
левая часть уравнения будет производной
функции
 :
:
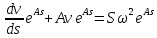
И
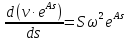
Тогда, интегрируя, получаем:
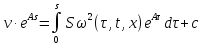
Следовательно,
функция
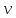 будет равна
будет равна
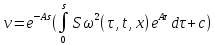
Подставляя
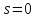 находим постоянную
находим постоянную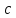 :
:
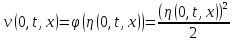
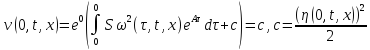
Тогда
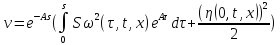
Итак, для программы численного решения исходного уравнения, потребуется три уравнения:
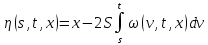
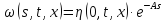

Возьмём
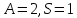 ,
тогда:
,
тогда:
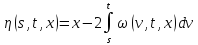
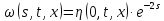
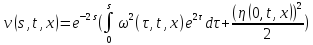
Программа
численного решения будет основываться
на методе последовательных приближений.
Поэтому запишем начальные функции,
которые будут использоваться для
вычисления начальных приближений
(подставляем в эти три уравнения
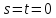 ):
):
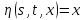
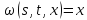
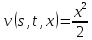
Уравнение
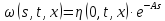
не
содержит функции
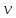 ,
поэтому можно ограничиться вычислением
,
поэтому можно ограничиться вычислением
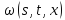 ,
и затем, пользуясь результатами вычислений
,
и затем, пользуясь результатами вычислений ,
найти
,
найти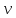 из уравнения:
из уравнения:
Дискретизация исходной задачи и её решение итерациями.
Для
нахождения функции
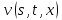 будут использоваться приближённые
сеточные функции. Для простоты
воспользуемся равномерной сеткой.
будут использоваться приближённые
сеточные функции. Для простоты
воспользуемся равномерной сеткой.
Задача
численных расчётов – найти значения
функции в узлах сетки и воспроизвести
результат на графике. Конечной целью
является графическое воспроизведение
функции
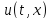 .
.
Введём
три индексные переменные
 ,
соответствующие переменным
,
соответствующие переменным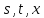 ,
где
,
где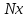 – число значений
– число значений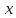 ,
а
,
а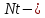 число значений
число значений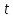 .
Также необходимо ввести не только
индексные, но и физические ограничения.
Для абсциссы это будет число
.
Также необходимо ввести не только
индексные, но и физические ограничения.
Для абсциссы это будет число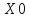 ,
а для времени –
,
а для времени – .
Значения
.
Значения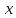 хранятся в массиве
хранятся в массиве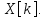
Для
того чтобы находить значения функции
в конкретной точке
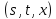 ,
необходимо инициализировать три массива:
,
необходимо инициализировать три массива:
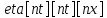 –массив
значений функции
–массив
значений функции
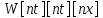 –массив
значений функции
–массив
значений функции
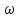
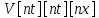 –массив
значений функции
–массив
значений функции
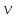
Зная,
что функции определены на равномерной
сетке нетрудно вычислить шаг сетки по
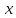 и по
и по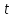 :
:
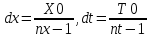
Опишем метод, на котором основано численное интегрирование сеточных функций. Пусть дана следующая задача:
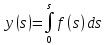
где
 – известная функция, а
– известная функция, а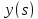 - неизвестная функция, которую нужно
определить. Сама функция
- неизвестная функция, которую нужно
определить. Сама функция представляетя собой некоторый график:
представляетя собой некоторый график:
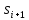
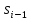
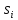



Известно,
что физический смысл интеграла – это
площадь криволинейной трапеции. Будем
рассматривать метод трапеций как
наиболее точный при небольшой затрате
процессорного времени на вычисления.
Зададим сеточные функции
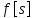 и
и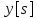 ,
,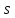 будем считать параметром массива, притом
будем считать параметром массива, притом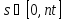 .
Очевидно, что при большом значении
.
Очевидно, что при большом значении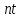 ,
а, следовательно, при большем количестве
узлов, мы получим более точное решение.
Итак, как известно, площадь трапеции
определяется по формуле:
,
а, следовательно, при большем количестве
узлов, мы получим более точное решение.
Итак, как известно, площадь трапеции
определяется по формуле:
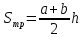
где
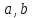 – стороны трапеции. В нашем случае мы
будем иметь следующую формулу:
– стороны трапеции. В нашем случае мы
будем иметь следующую формулу:
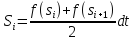
Теперь
можно записать окончательную формулу
для
 :
:
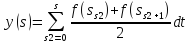
В
нашей программе, соответсвенно, все
интегралы будем считать с помощью цикла
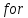 .
.
