
- •Введение.
- •Постановка начальной задачи.
- •Применение метода дополнительного аргумента к решению характеристической системы.
- •Доказательство эквивалентности систем (8) и (26).
- •Доказательство существования решения задачи Коши
- •Постановка задачи численного расчёта.
- •Дискретизация исходной задачи и её решение итерациями.
- •Программа и её описание. Результаты вычислений.
- •Заключение.
- •Литература
- •Оглавление
Доказательство эквивалентности систем (8) и (26).
Покажем, что если
решением системы уравнений (26) являются
непрерывно-дифференцируемые и ограниченные
вместе со своими первыми производными
функции
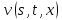 и
и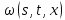 ,
то функции
,
то функции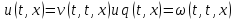 ,
будут решением задачи Коши (8), (2), (9) при
,
будут решением задачи Коши (8), (2), (9) при где
где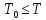 .
.
Продифференцируем
(22) по
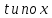 :
:
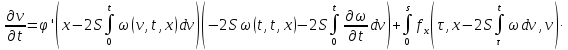

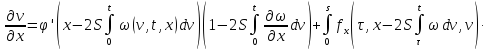
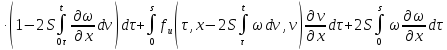
Умножим второе
равенство на
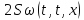 :
:
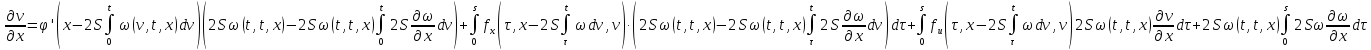
Получившееся равенство сложим с первым:
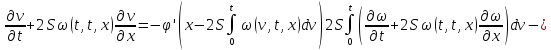
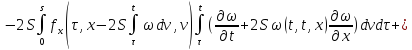
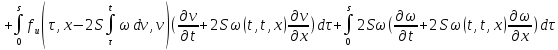
Обозначим через
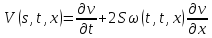 ,
а через
,
а через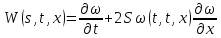 тогда последнее равенство перепишется
в виде:
тогда последнее равенство перепишется
в виде:

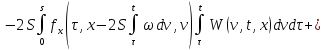
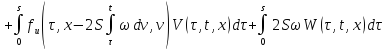
Аналогично
продифференцируем (23) по
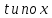 :
:
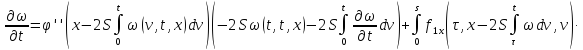
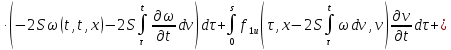
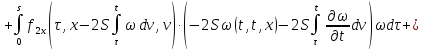
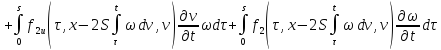
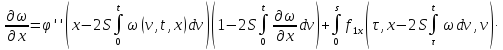
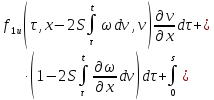
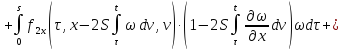
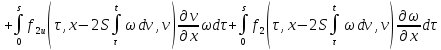
Умножим второе
равенство на
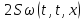 :
:
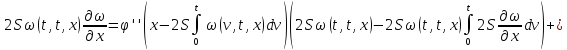

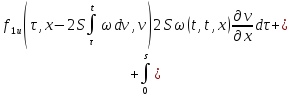
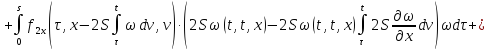

Сложим получившееся равенство с первым:

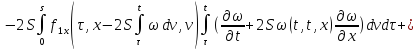

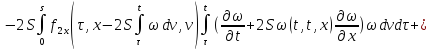
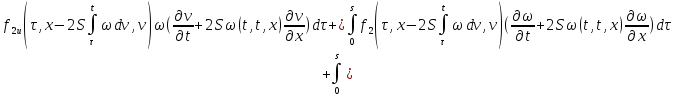
Последнее равенство
с учётом обозначений
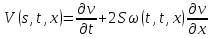 ,
,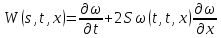 перепишем в виде:
перепишем в виде:
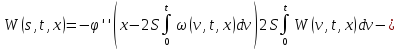
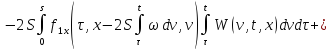
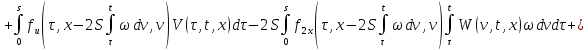
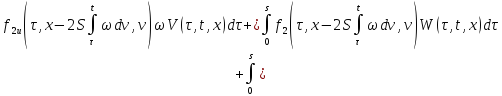
Итак, получили два
уравнения от двух неизвестных функций
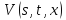 и
и :
:
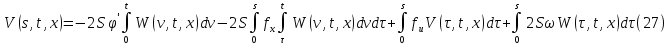


Обозначим через:
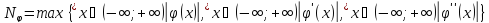
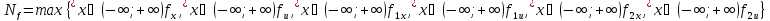

Тогда из (27) и (28):


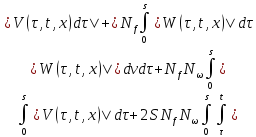
Или:
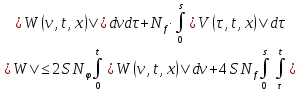
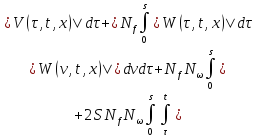
Меняя порядок интегрирования, будем иметь:
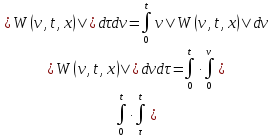
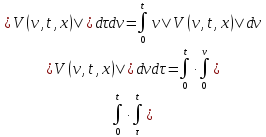
Обозначим через
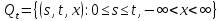 ,
тогда для всех
,
тогда для всех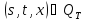
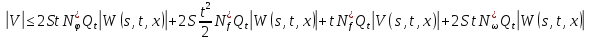
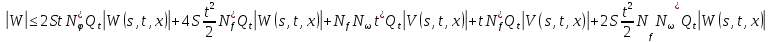
Обозначим через
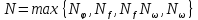 ,
тогда:
,
тогда:


Складывая, получаем:
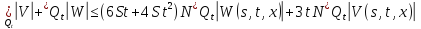
Обозначим через
 .
Очевидно, что для любого
.
Очевидно, что для любого
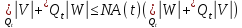
Обозначим через
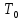 значениеt,
при котором
значениеt,
при котором
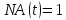 .
Тогда для любыхt
из промежутка
.
Тогда для любыхt
из промежутка
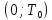
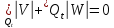 ,
то есть
,
то есть
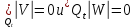 ,
следовательно, что для любого
,
следовательно, что для любого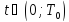 выполняются тождества:
выполняются тождества:
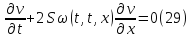
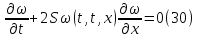
Подставим функции
 :
:
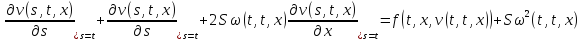
С учётом равенств (29) и (24), получим тождество:
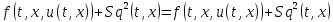
Аналогично для второго уравнения системы:
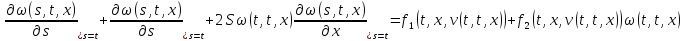
Учитывая (30) и (25), получим тождество:
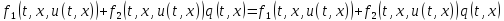
Проверим, что функции
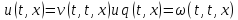 удовлетворяют начальным условиям (2) и
(9). Для этого подставим в (26)
удовлетворяют начальным условиям (2) и
(9). Для этого подставим в (26)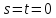 .
.
В результате приходим к равенствам:
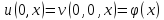

которые подтверждают, что решение системы (26) удовлетворяет начальным условиям (2), (9).
Итак,
мы доказали, что решение задачи (8), (2),
(9) даёт решение системы (26), и наоборот,
непрерывно дифференцируемое решение
системы (26) при )
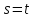 будет решением задачи (8), (2), (9). То есть
эквивалентность двух систем показана.
будет решением задачи (8), (2), (9). То есть
эквивалентность двух систем показана.
Доказательство существования решения задачи Коши
Осталось доказать существование ограниченного непрерывно дифференцируемого решения системы уравнений (26), тем самым будет доказано существование классического решения задачи Коши (1), (2).
Введём некоторые обозначения и определения.
Будем обозначать
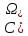 )
и
)
и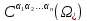 –
пространства функций определённых и
непрерывных (соответственно со своими
производными до порядка
–
пространства функций определённых и
непрерывных (соответственно со своими
производными до порядка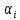 по
по му
аргументу,
му
аргументу,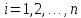 )
на некотором подмножестве
)
на некотором подмножестве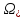 евклидова
пространства,
евклидова
пространства,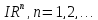 .
.
Введём следующие обозначения:
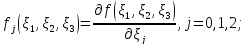

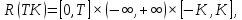
где
 – произвольно зафиксированное
положительное число,
– произвольно зафиксированное
положительное число,
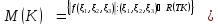
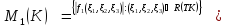

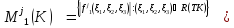
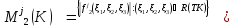
Также будем пользоваться ранее введённым обозначением:

Для произвольной
функции
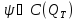 и
и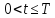 мы положим:
мы положим:
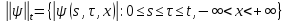
Лемма 1. Пусть
 ,
,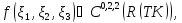 причем
причем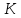 и
и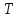 подобраны таким образом, что выполняются
неравенства
подобраны таким образом, что выполняются
неравенства
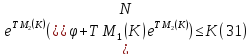
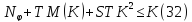
Пусть, далее
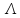 – положительный корень уравнения
– положительный корень уравнения
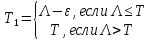
где
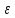 - любое число из интервала (0,
- любое число из интервала (0,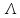 )
)
и для любого

где

Тогда при
 система
уравнений (26) имеет единственное решение.
система
уравнений (26) имеет единственное решение.
Доказательство.
Будем доказывать существование решения системы уравнений (26) методом последовательных приближений. Положим:
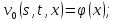
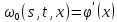
и будем строить последовательности функций
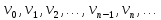
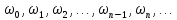
таким образом, что
для всех
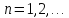
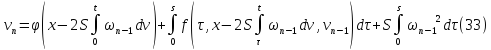

или
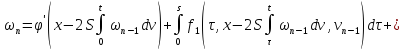
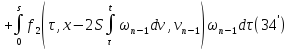
В силу (31), (32) из (34)
и (33) все
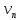 ,
,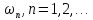 будут ограничены:
будут ограничены:
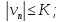
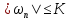
Будем доказывать, что последовательные приближения сходятся. Найдём разность:
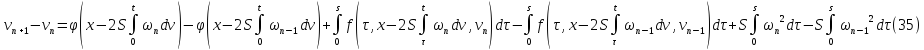

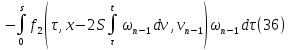
Заметим, что функция
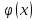 имеет
ограниченные производные на
имеет
ограниченные производные на ,
поскольку
,
поскольку ,
а
,
а
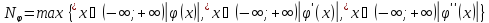
следовательно,
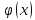 удовлетворяет условию Липшица с
константой
удовлетворяет условию Липшица с
константой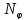 :
:
|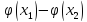 |=|
|=|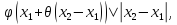
где
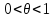 ,
а значит
,
а значит
|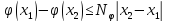
Аналогично для
функции
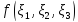 ,
,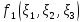 ,
,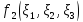 :
:
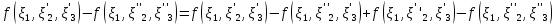
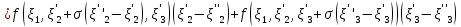 .
.
Из этого равенства выводим, что
|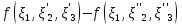 |
|
|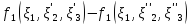 |
|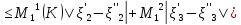
|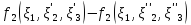 |
|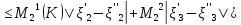
Из двух последних слагаемых (36):
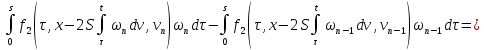
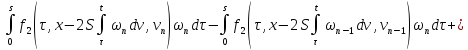
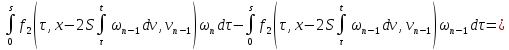
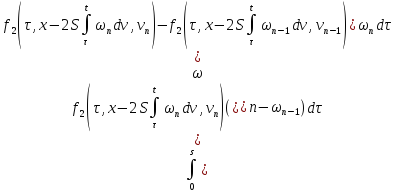
С учётом этих равенств получим из (36)
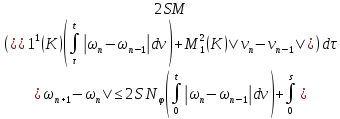
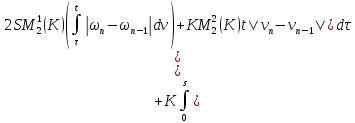
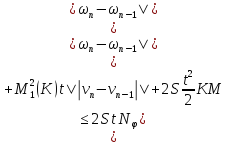
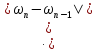
То есть:
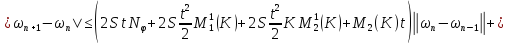
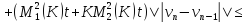
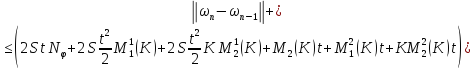
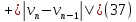
Аналогично из (35):
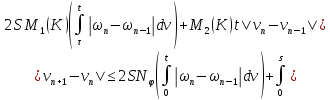
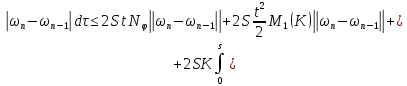

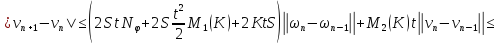
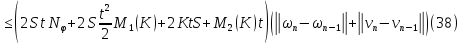
Сложим последние равенства (37) и (38):
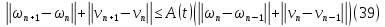
где
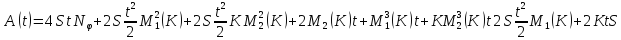
Рассмотрим вектор
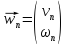 .
Будем доказывать, что последовательные
приближения
.
Будем доказывать, что последовательные
приближения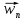 сходятся по норме к вектору
сходятся по норме к вектору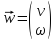 .
За норму вектора
.
За норму вектора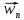 положим сумму норм
положим сумму норм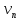 и
и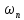 :
:
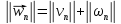
Тогда с учётом введённых обозначений равенство (39) перепишется в виде:
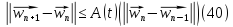
Пусть
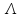 - положительный корень уравнения
- положительный корень уравнения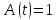 .
Тогда при любом
.
Тогда при любом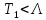 ряд
ряд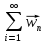 сходится к вектору
сходится к вектору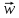 .
Именно, мы можем представить
.
Именно, мы можем представить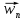 в виде суммы:
в виде суммы:
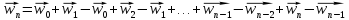
Ряд
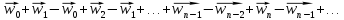
мажорируется
сходящимся (так как
 рядом
рядом
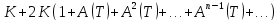
(здесь взято
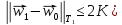 .
.
Это означает, что
его частичная сумма сходится к вектору
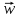 по норме.
по норме.
А это и означает,
что ряды
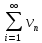 и
и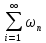 также сходятся соответственно к функциям
также сходятся соответственно к функциям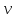 и
и по норме. Перейдя к пределу в равенствах
(33) и (34), получим, что функции
по норме. Перейдя к пределу в равенствах
(33) и (34), получим, что функции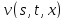 и
и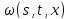 ,
будут удовлетворять системе (26).
,
будут удовлетворять системе (26).
Единственность следует из того факта, что для разности двух возможных решений системы (26) будет выполняться неравенство вида
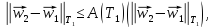
где .
.
Лемма 2. При
выполнении условий леммы 1
 ,
,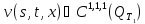 .
.
Доказательство.
Согласно (25) функция
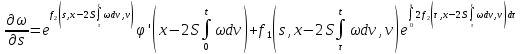
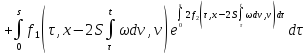
непрерывна и
ограничена в
 (так
как она получается из известных
непрерывных и ограниченных функций с
помощью конечного числа арифметических
операций и композиций).
(так
как она получается из известных
непрерывных и ограниченных функций с
помощью конечного числа арифметических
операций и композиций).
С учётом этого функция
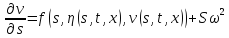
также непрерывна и
ограничена в
 .
.
Чтобы доказать
существование, непрерывность и
ограниченность частных производных
функций
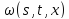 и
и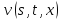 продифференцируем по
продифференцируем по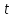 соотношения, определяющие соответствующие
последовательные приближения:
соотношения, определяющие соответствующие
последовательные приближения:
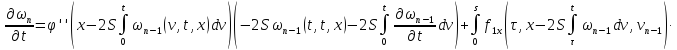
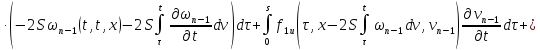
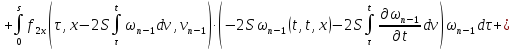
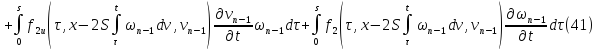
С учетом того, что
|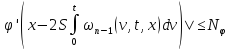
|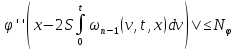
|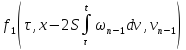 |
|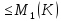
|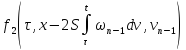 |
|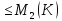
|
|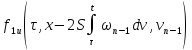 |
|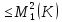
|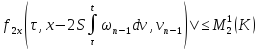
|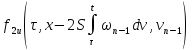 |
|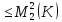
|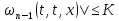
получаем:
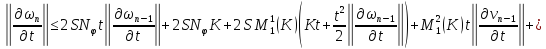
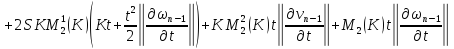
Приводя подобные, получаем:

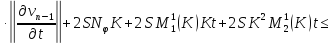
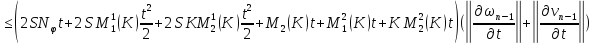
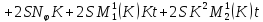
Аналогично для
функции
 :
:
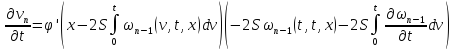

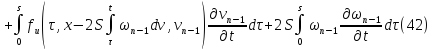
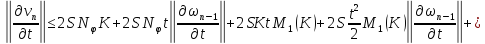
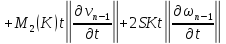
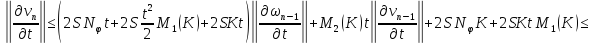
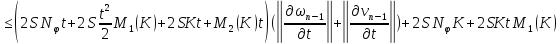
Складывая получившиеся равенства, получаем:
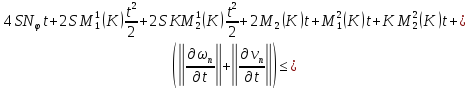
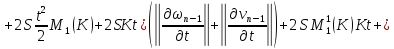
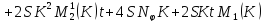
Вспоминая, что
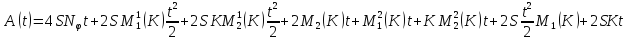
а также, что
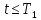
получаем:
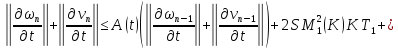
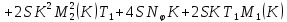
Обозначая за
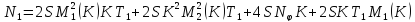
Снова введём в
рассмотрение вектор
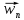 .
За его норму положим сумму норм
.
За его норму положим сумму норм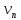 и
и
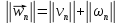
Тогда получаем:
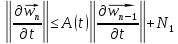
При
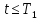 имеем
имеем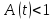
Далее, так как
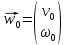 ,
а
,
а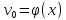 ,
, ,
то
,
то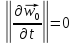 ,
поэтому
,
поэтому
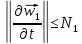
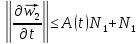
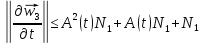
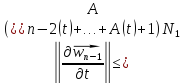
Пользуясь формулой бесконечно убывающей геометрической прогрессии, будем иметь:

А это означает, что
последовательность
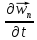 ограничена по норме. Следовательно,
ограничены по норме и последовательности
ограничена по норме. Следовательно,
ограничены по норме и последовательности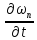 и
и .
.
Чтобы несколько
облегчить доказательство её сходимости,
рассмотрим вначале линейные интегральные
уравнения относительно неизвестных
функций
 и
и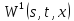 и рассмотрим вектор
и рассмотрим вектор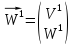
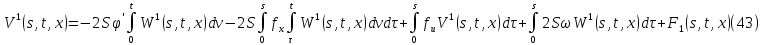
где

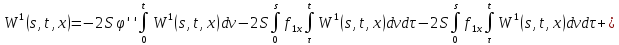

где
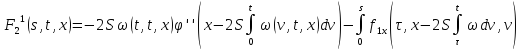

С помощью метода
последовательных приближений доказывается,
что уравнения (39) и (40) имеют решения,
принадлежащие пространству
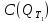 .
.
Из равенств (42) и (43):
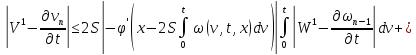
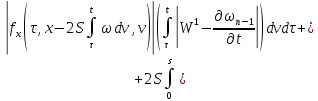

где
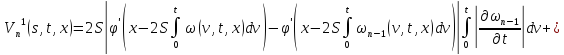
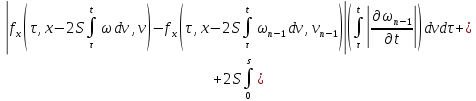
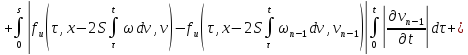
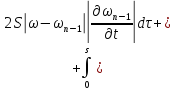
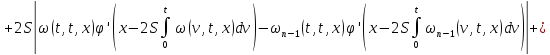
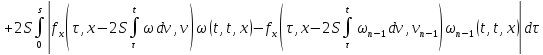
Аналогично из равенств (41) и (44):
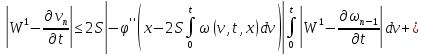
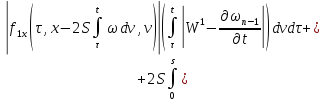
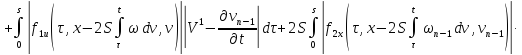
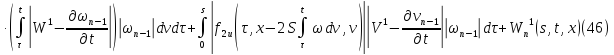

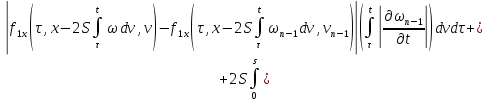
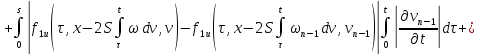
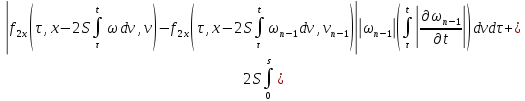
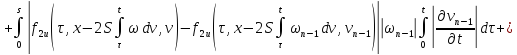
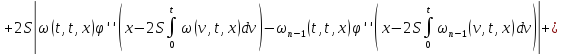
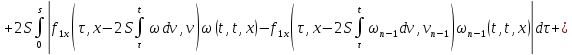
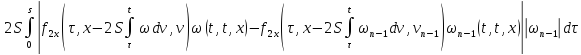
В силу сходимости
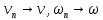 и ограниченности
и ограниченности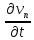 и
и при всех
при всех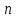 для любого
для любого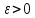 можно определить такой номер
можно определить такой номер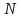 ,
что для всех
,
что для всех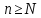 будет:
будет:
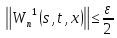
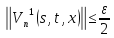
Переходя к норме в неравенствах (45) и (46), получаем
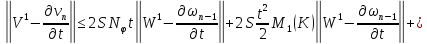

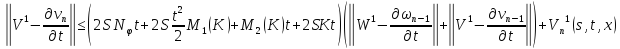
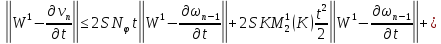

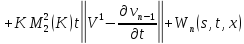
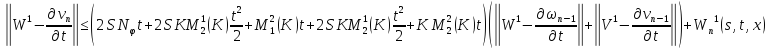
Складывая получившиеся неравенства и вспоминая, что
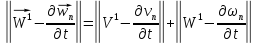
получаем, что для
всех
 будет выполняться неравенство:
будет выполняться неравенство:

При
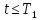 имеем
имеем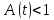 ,
поэтому из предыдущего неравенства
вытекает:
,
поэтому из предыдущего неравенства
вытекает:
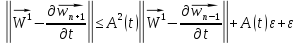
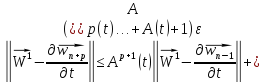
Таким образом, для
любого
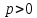 будет
выполняться неравенство:
будет
выполняться неравенство:
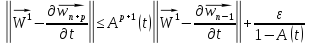
В силу того, что
 для любого числа
для любого числа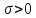 можно определить такой номер
можно определить такой номер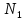 ,
что для всех
,
что для всех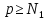 будет
будет
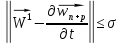
Этим самым мы
доказали, что последовательность
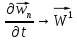 при
при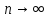 ,
а значит и последовательности
,
а значит и последовательности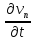 и
и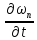 сходятся соответственно к функциям
сходятся соответственно к функциям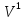 и
и .
.
Точно также
доказывается сходимость последовательностей
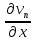 и
и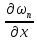 к некоторым функциям
к некоторым функциям и
и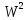 :
:
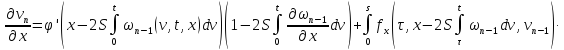

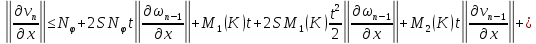
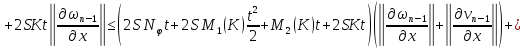
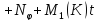


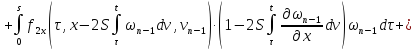
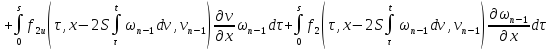
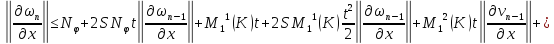

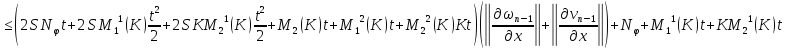
Складывая получившиеся неравенства, получаем:

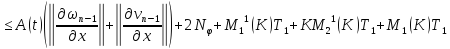
Обозначим
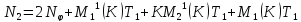
Тогда неравенство перепишется в виде:
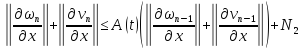
То есть
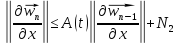
При
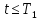 имеем
имеем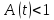
Далее, так как
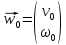 ,
а
,
а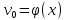 ,
,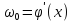 ,
то
,
то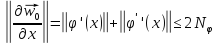 ,
поэтому
,
поэтому
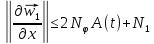
Обозначим
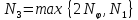
Тогда неравенство перепишется в виде:
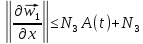
Увеличивая число
 ,
получаем:
,
получаем:

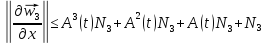

Пользуясь формулой бесконечно убывающей геометрической прогрессии, будем иметь:
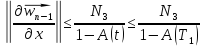
А это означает, что
последовательность
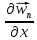 ограничена по норме. Следовательно,
ограничены по норме и последовательности
ограничена по норме. Следовательно,
ограничены по норме и последовательности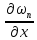 и
и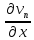 .
.
Чтобы несколько
облегчить доказательство её сходимости,
рассмотрим вначале линейное интегральное
уравнение относительно неизвестных
функций
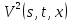 и
и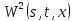 и рассмотрим вектор
и рассмотрим вектор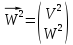
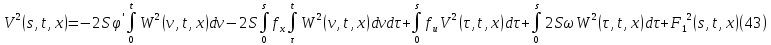
где
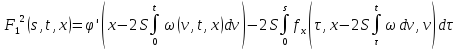

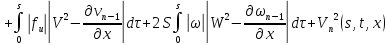
где
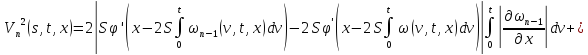
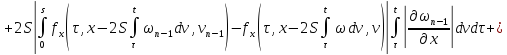

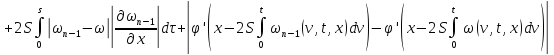

Аналогично для
последовательности
 :
:
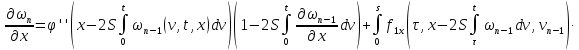
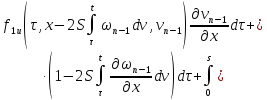

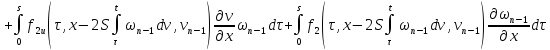
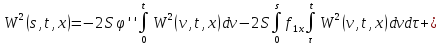

где
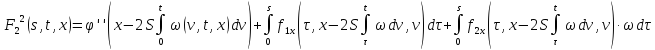

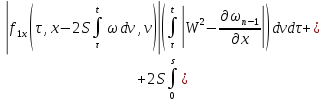


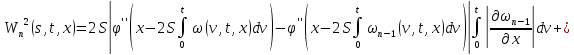
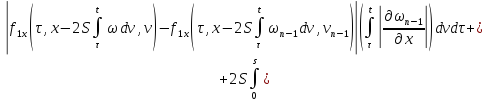
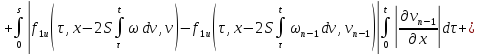
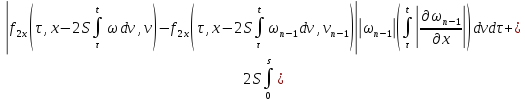

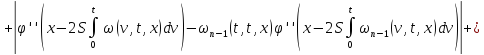
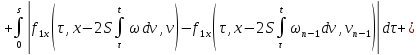
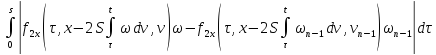
В силу сходимости
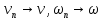 и ограниченности
и ограниченности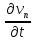 и
и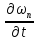 при всех
при всех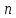 для любого
для любого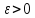 можно определить такой номер
можно определить такой номер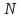 ,
что для всех
,
что для всех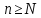 будет:
будет:
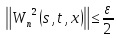
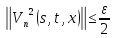
Переходя к норме в неравенствах (45) и (46), получаем
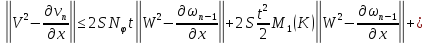
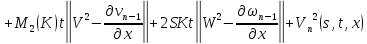
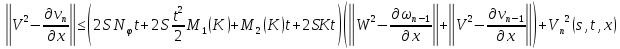
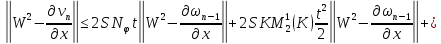

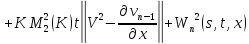

Складывая получившиеся неравенства и вспоминая, что
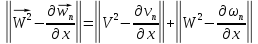
получаем, что для
всех
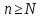 будет выполняться неравенство:
будет выполняться неравенство:
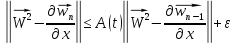
При
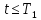 имеем
имеем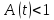 ,
поэтому из предыдущего неравенства
вытекает:
,
поэтому из предыдущего неравенства
вытекает:
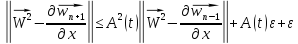
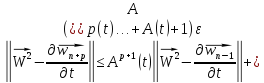
Таким образом, для
любого
 будет
выполняться неравенство:
будет
выполняться неравенство:
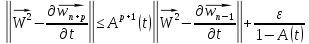
В силу того, что
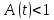 для любого числа
для любого числа можно определить такой номер
можно определить такой номер ,
что для всех
,
что для всех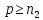 будет
будет
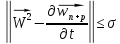
Этим самым мы
доказали, что последовательность
 при
при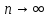 ,
а значит и последовательности
,
а значит и последовательности и
и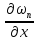 сходятся соответственно к функциям
сходятся соответственно к функциям и
и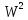 .
.
В
результате для последовательностей
{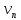 }
и {
}
и {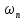 }
установлены следующие свойства:
}
установлены следующие свойства:
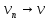
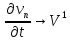
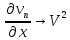
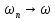
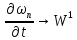
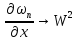
Имеем:
последовательность
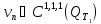 ,
при любом
,
при любом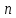 сходится по норме этого пространства.
В силу полноты и замкнутости пространства
сходится по норме этого пространства.
В силу полноты и замкнутости пространства имеем, что
имеем, что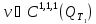 ,
а значит, обладает частными производными
по
,
а значит, обладает частными производными
по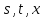 ,
причём
,
причём
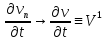
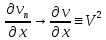
Аналогично
 ,
а значит
,
а значит

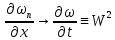
Таким образом, лемма 2 доказана.
На основе этих двух лемм и всего вышеизложенного, можно сформулировать общую теорему:
Теорема
1. Пусть на области
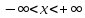 и
и задано нелинейное дифференциальное
уравнение:
задано нелинейное дифференциальное
уравнение:
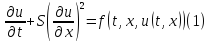
И пусть задано следующее начальное условие
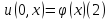
Если:
Функция
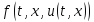 непрерывна, ограничена, дважды непрерывно
дифференцируема по переменным
непрерывна, ограничена, дважды непрерывно
дифференцируема по переменным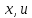 и все вторые, а также смешанные производные
удовлетворяют по этим переменным
условию Липшица и ограничены при всех
значениях аргументов.
и все вторые, а также смешанные производные
удовлетворяют по этим переменным
условию Липшица и ограничены при всех
значениях аргументов.Пусть функция
 дважды непрерывно дифференцируема на
дважды непрерывно дифференцируема на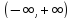 ,
а её вторая производная ограничена и
удовлетворяет условию Липшица.
,
а её вторая производная ограничена и
удовлетворяет условию Липшица.
Тогда существует
такая константа
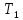 ,
что при
,
что при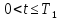 задача (1) – (2) имеет единственное
непрерывное и ограниченное вместе со
своими первыми производными решение,
которое совпадает при
задача (1) – (2) имеет единственное
непрерывное и ограниченное вместе со
своими первыми производными решение,
которое совпадает при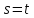 с функцией
с функцией ,
определяемой из системы интегральных
уравнений (26).
,
определяемой из системы интегральных
уравнений (26).
