Введение.

Разработано несколько разных методов для исследования разрешимости нелинейных дифференциальных уравнений в частных производных первого порядка. Например, всем известный классический метод характеристик, метод Галеркина, метод потоков. Как и любой метод, каждый из них имеет свои преимущества и свои недостатки. Нельзя выделить какой-либо метод, позволяющий решать любые дифференциальные уравнения в частных производных первого порядка. Каждый из известных методов хорошо применим только к определенному классу уравнений. Если, например, обратиться к тому же самому методу характеристик, то оказывается, что он с успехом применяется лишь в случае, когда коэффициенты перед производными не содержат неизвестных функций. А для систем квазилинейных дифференциальных уравнений или решения нелинейных дифференциальных уравнений реально его применять довольно сложно. В первую очередь, это связано с тем, что при применении метода характеристик для таких уравнений в соответствующем интегральном уравнении появляется суперпозиция неизвестных функций. В последнее время широкое развитие получил, в частности, метод дополнительного аргумента. Он позволяет свести решение исходной задачи к интегральному уравнению или системе интегральных уравнений. В этом уравнении неизвестная функция зависит от трех независимых переменных, но сами уравнения достаточно простые по своей структуре. Для них достаточно просто доказать существование дифференцируемого решения, исследовать качественные свойства решения, а также построить численное решение. В частности, для этого можно использовать метод последовательных приближений. Сущность метода дополнительного аргумента, его применение к решению нелинейных дифференциальных уравнений рассматриваются далее.

Постановка начальной задачи.

В области ирассмотрим нелинейное дифференциальное уравнение:

И пусть задано следующее начальное условие

Продифференцируем данное уравнение по х:

Обозначим Тогда уравнение (3) перепишется в виде:

Исходное уравнение (1) в наших новых обозначениях перепишется так:

Преобразуем его так:

Запишем характеристическую систему для уравнения (1) относительно неизвестных функций :

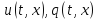Таким образом, нелинейное уравнение (1) м свели к системе из двух квазилинейных уравнений (8). С учётом (2) зададим начальное условие для функции :

Покажем, что функция , определяемая системой уравнений (8) и начальными условиями (2) и (9), будет являться искомым решением уравнения (1) с начальным условием (2). Для этого достаточно показать, что

Продифференцируем первое уравнение системы по x:

(10)

Вычтем из получившегося равенства второе уравнение системы:

(11)

Обозначим через , тогда из равенство (11) перепишется в виде:

или:

При всех и функция ограничена. Кроме того,

.

Значит, можно определить константу , что при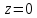. А это и означает, что , а значит функция , определяемая системой уравнений (8) и начальными условиями (2) и (9), будет являться искомым решением уравнения (1) с начальным условием (2), что и требовалось доказать.

Применение метода дополнительного аргумента к решению характеристической системы.

Применяя метод характеристик к обоим уравнениям системы (8), получим следующую систему из трёх уравнений:

(13)

Исследуем начальную задачу (8), (2), (9) при помощи метода дополнительного аргумента. Введём следующие обозначения:

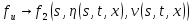
То есть рассмотрим следующую систему дифференциальных уравнений относительно неизвестных функций :

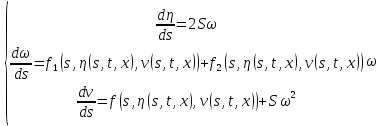(14)

Второе уравнение системы (14) можно рассматривать как линейное неоднородное уравнение первого порядка относительно функции , которая зависит от. Тогда методом Эйлера (метод интегрирующего множителя) можно найти:

Далее, будем искать такое решение системы, которое при 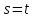перейдёт в точку, то есть

Также будем учитывать и другие начальные условия:

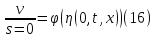
(17)

Пользуясь формулой Ньютона-Лейбница из первого уравнения системы (14) получим следующее интегральное уравнение:

=(18)

Из условия (15) , поэтому уравнение (18) можно переписать в виде:

=(19)

Из второго уравнения системы (14) аналогично получим следующее интегральное уравнение:

(20)

Из (17) , а из (19) приполучим=, а значити уравнение (20) перепишется в виде:

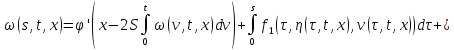
(21)

Снова используя формулу Ньютона-Лейбница, получим =и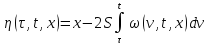. Поэтому (21) можно переписать так:

(22)

Совершенно аналогично переходим от третьего уравнения системы (14) к уравнению (23):

(23)

Из (23) вытекает, что

Аналогично из (22):

Итак, мы перешли к следующей системе из двух уравнений: