
3.5. Метод Ньютона
Задан отрезок [a,b], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [a,b], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(x0)*F(x0)>0). В точке F(x0) строится касательная к кривой y= F(x) и ищется ее пересечение с осью x. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:
![]()
Итерационный процесс продолжается до тех пор, пока не будет выполнено условие F(x)<, где- заданная точность.
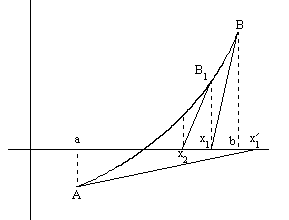
Рис. 3.6. Иллюстрация метода Ньютона (1)
В качестве начального приближения можно взять также середину отрезка [a,b]:
![]()
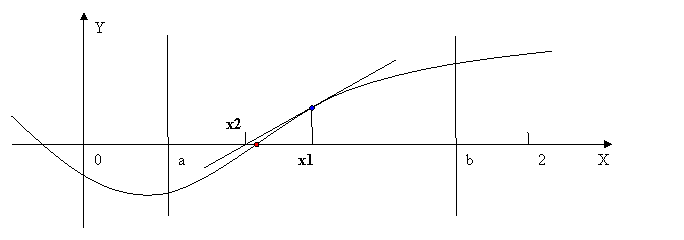
Рис. 3.7 Иллюстрация метода Ньютона(2)
Если на отрезке
существования корня знаки
![]() и
и![]() не изменяются, то начальное приближение,
обеспечивающее сходимость, нужно выбрать
из условия
не изменяются, то начальное приближение,
обеспечивающее сходимость, нужно выбрать
из условия
![]() ,
x0[a;b].
,
x0[a;b].
т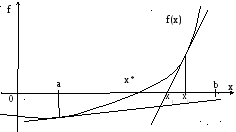 .е.
в точке начального приближения знаки
функций и ее второй производной должны
совпадать.
.е.
в точке начального приближения знаки
функций и ее второй производной должны
совпадать.
Рис. 3.13. Геометрическая
иллюстрация выбора начального приближения:
график f(x) вогнутый,
![]() ,
тогда x0=b, т.к. f(b)>0.
,
тогда x0=b, т.к. f(b)>0.
Если же выбрать x0=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x0=a).

●
Рис. 3.14. Геометрическая иллюстрация выбора начального приближения: график f(x) выпуклый, f ’’(x)<0 , тогда x0 =a, т.к. f(a)<0.
Метод Ньютона в отличие от ранее рассмотренных методов используют свойства функции в виде значения производной, что значительно ускоряет итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции), тем быстрее сходимость.
Рассмотрим пример ручной реализации метода. Дано уравнение x2– 4x+ 3 = 0. Известно, что корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом Ньютона с точностью= 0,001.
Найдем первую и вторую производную функции F(x).F’(x)= 2x– 4;F”(x) = 2.F(0,9) = 0,21;F(1,2) = -0,36. Следовательно, в качестве начального приближения выбираем точкуx0=a= 0,9. Построим таблицу в соответствии с алгоритмом метода.
-
i
xi
F(xi)
F'(xi)
F(xi)<0,001
0
0,9
0,21
-2,2
нет
1
0,99545
0,00911
-2,0090909
нет
2
0,99999
0,000021
-1,00002
да
Ответ: уточненное значение корня x0,99999.
Достоинство метода:очень быстрая сходимость к заданной точности.
Недостатки: громоздкий алгоритм: на каждой итерации необходимо вычислять значение функции и ее первой производной, сильная зависимость сходимости от вида функции и выбора начального приближения.
3.6. Метод простой итерации
Метод основан на замене исходного уравнения F(x)=0 на эквивалентноеx=(x). Функция(x) выбирается таким образом, чтобы на обоих концах отрезка [a,b] выполнялось условие сходимости(x)< 1. В этом случае в качестве начального приближения можно выбрать любой из концов отрезка. Итерационная формула имеет вид
![]()
Итерационный процесс продолжается до тех пор, пока не будет выполнено условие F(x)<, где- заданная точность.
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение представим на графике в виде двух функций: y1 = x и y2= φ(x).
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рисунках
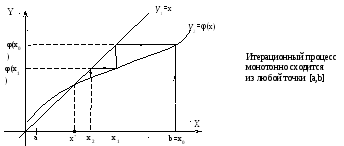

Рис. 3.8 Итерационный
процесс для случая 0<![]() <1
<1![]() x[a,b].
x[a,b].

Рис. 3.9 Итерационный
процесс для случая -1<![]() <1
<1![]() x[a,b].
x[a,b].
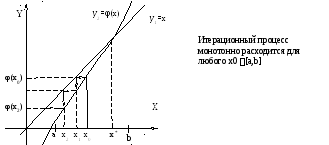
Р ис.
3.10. Итерационный процесс для случая
ис.
3.10. Итерационный процесс для случая![]() >1
>1![]() x[a,b].
x[a,b].
Рис. 3.11. Иллюстрация метода простой итерации
Из анализа графиков
следует, что скорость сходимости растет
при уменьшении значения
![]()
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование чтобы обеспечивалось условие сходимости. Простейшие эквивалентные преобразования, например:
f(x) = 0 => x+f(x) = x, т.е. φ(x) = x + f(x)
или выразить явно x
f(x) = 0 => x - φ(x) = 0 => x = φ(x)
не гарантируют сходимость.
Рекомендуется следующий способ получения формулы сходящегося итерационного процесса.
П![]() усть
усть![]() .
.
Если это не так, умножить обе части уравнения на и к обеим частям прибавить x:
![]()
Константу вычислить по формуле:
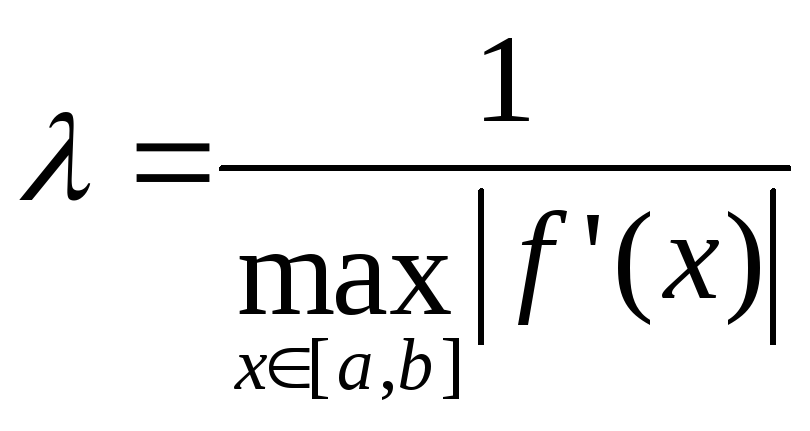
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
xi = xi+1− λ f(x)
где i=1,2,… - номер итерации, x0[a,b] – начальное приближение.
Рассмотрим пример ручной реализации метода. Дано уравнение x2 – 4x + 3 = 0. Известно, что корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом простой итерации с точностью = 0,03.
На первом этапе нам необходимо выбрать функцию (x), удовлетворяющую условию сходимости.
Запишем исходное уравнение в виде x = x2 – 3x + 3. Тогда (x) = x2 – 3x + 3;(x) = 2x – 3;(0,9) = -1,2;(1,2) = -0,6. Условие сходимости не выполнено, поскольку-1,2> 1.
Запишем исходное
уравнение в виде
![]() .
Тогда
.
Тогда![]() Условие сходимости не выполнено,
поскольку2,6> 1;1,5> 1.
Условие сходимости не выполнено,
поскольку2,6> 1;1,5> 1.
Запишем исходное
уравнение в виде
![]() Условие
сходимости выполнено.
Условие
сходимости выполнено.
Следовательно, итерационная формула имеет вид:
![]()
В качестве начального приближения можно выбрать любой из концов отрезка, например x0=a= 0,9. Построим таблицу в соответствии с алгоритмом метода.
-
i
xi
F(xi)
IF(xi)I<0,03
0
0,9
0,21
нет
1
0,9525
0,0973
нет
2
0,9768
0,0469
нет
3
0,9885
0,0230
да
Ответ: уточненное значение корня x0,9885.
