Министерство образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Нижегородский Государственный Технический Университет им. Р.Е. Алексеева»

Кафедра «Прикладная математика»

Реферат по теме

«Конформные отображения»

Выполнила:

Студентка 2 курса

ИРИТ, группа 10 – ПМ

Багрова Екатерина

Проверил:

Алексеенко С. Н.

Нижний Новгород, 2012 г.

Содержание

1. Геометрический смысл производной функции комплексного переменного.

   0. Геометрический смысл аргумента производной.

   1. Геометрический смысл модуля производной.

2. Понятие конформного отображения.

3. Общие свойства конформных отображений.

4. Основные функции.

   0. Линейная функция.

   1. Дробно-линейная функция.

   2. Степенная функция. Понятие римановой поверхности.

   3. Показательная и логарифмическая функции.

      0. Показательная функция.

      1. Логарифмическая функция.

   4. Общая степенная и тригонометрические функции. Функция Жуковского.

      0. Общая степенная функция.

      1. Тригонометрические функции.

      2. Обратные тригонометрические функции.

      3. Функция Жуковского.

1. Геометрический смысл производной функции комплексного переменного.

1. Геометрический смысл аргумента производной.

Напомним вначале некоторые сведения о кривых. Каждая кривая на плоскости может быть задана параметрическими уравнениями

x = x (t), y = y (t), α ≤ t ≤ β , (1)

где x (t), y (t) — действительные функции действительного переменного t. В дальнейшем предполагается, что эти функции имеют непрерывные производные на интервале (α, β), причем x’(t) и y’(t) не обращаются в нуль одновременно. Кривая, обладающая указанными свойствами, называется гладкой.

Так как каждая точка (х, у) на плоскости задается комплексным числом z = х + iy, то уравнения (1) можно записать в более компактной форме:

z (t) = x (t) + i y (t), α ≤ t ≤ β.

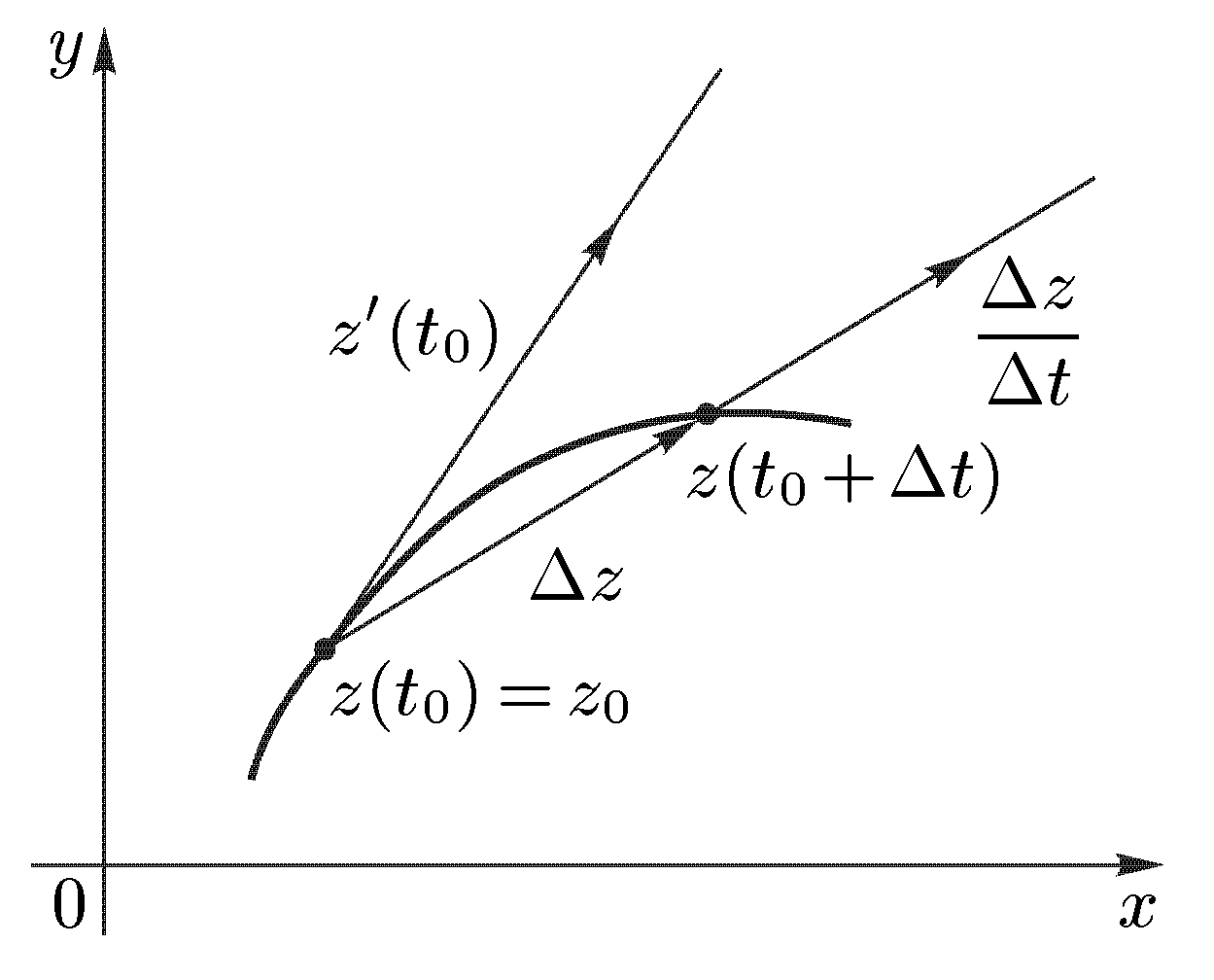Возьмем значения t₀ и t₀ + Δt из интервала (α, β). Им соответствуют точки z (t₀) и z (t₀ + Δ t) на кривой.

Вектор Δz = z (t₀ + Δt) – z (t₀) = Δx + i Δy направлен по секущей, проходящей через эти точки.

Если умножить Δz на действительное число 1/ Δt, то получим вектор Δz / Δt, коллинеарный вектору Δz. Начнем уменьшать Δt. Тогда точка z (t₀ + Δt) будет приближаться к z (t₀) по кривой; вектор Δz/ Δt будет поворачиваться, приближаясь к вектору

.

Предельное положение секущих, проходящих через точку z (t₀), называется касательной к кривой в этой точке. Таким образом, вектор z ' (t₀) направлен по касательной к кривой в точке z (t₀).

Пусть теперь задана функция f (z), аналитическая в точке z₀, причем f ’(z₀) ≠ 0. Предположим далее, что через точку z₀ проходит кривая γ, заданная уравнением z (t) = x (t) + iy (t), и z (t₀) = z₀. Кривая γ отображается функцией w = f (z) в кривую Г, лежащую в плоскости переменного w; уравнение кривой Г будет иметь вид w (t) = f (z(t)); точка z₀ отобразится в точку w₀ = f (z₀). По правилу дифференцирования сложной функции

w ' (t₀) = f ' (z₀) · z ' (t₀). (2)

Отсюда следует, что

Arg w ' (t₀) = Arg f ' (z₀) + Arg z ' (t₀). (3)

Но z ' (t₀) есть вектор, касательный к кривой γ в точке z₀ (рис. 1а), a w ' (t₀) — вектор, касательный к кривой Г в точке w₀ (рис. 1б). Поэтому равенство (3) позволяет придать величине Arg f ' (z₀) следующий геометрический смысл: аргумент производной равен углу, на который поворачивается касательная в точке z₀ к любой кривой, проходящей через эту точку, при отображении w = f (z). Заметим, что этот угол не зависит от кривой γ, т.е. касательные ко всем кривым, проходящим через точку z₀, поворачиваются при отображении w = f (z) на один и тот же угол, равный Arg f ' (z₀).

Возьмем какие-либо две кривые γ и γ1 проходящие через точку z₀, и проведем касательные к этим кривым (рис. 1а). При отображении

(рис. 1)

w = f (z) кривые γ и γ1 перейдут в кривые Г и Г₁, а каждая из касательных к γ и γ1 повернется на один и тот же угол. Поэтому угол θ между касательными к γ и γ1 будет равен (как по величине, так и по направлению отсчета) углу между касательными к Г и Г_1. Напомним, что углом между кривыми в точке z₀ называется угол между касательными к этим кривым в точке z₀. Таким образом, если f ’(z₀) ≠ 0, то отображение w = f (z) сохраняет углы между кривыми. Заметим, что при этом сохраняется не только абсолютная величина углов между кривыми γ и γ1 и их образами, но и направление углов. Это свойство данного отображения носит название свойства сохранения углов.

2. Геометрический смысл модуля производной.

Зафиксируем точку z₀ и возьмем приращение аргумента Δz; очевидно, что модуль |Δz| равен расстоянию между точками z₀ и z = z₀ + Δz (рис. 2а). Пусть w = f (z), Δw = w — w₀. Тогда величина |Δw| / |Δz| указывает, в каком отношении изменяется расстояние между точками z₀ и z в результате отображения w = f (z). Предел называется коэффициентом растяжения в точке z₀ при отображении w = f (z). Поскольку

,

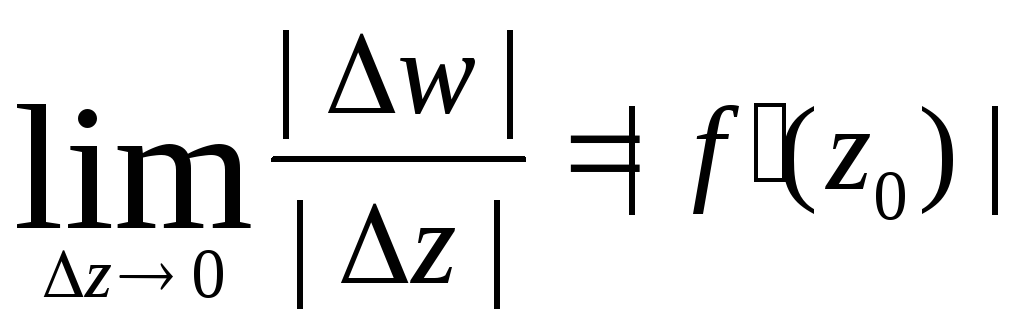то модуль | f ’(z₀) | равен коэффициенту растяжения в точке z₀ при отображении w = f (z). Если | f ’(z₀) | > 1, то в достаточно малой окрестности точки z₀ расстояния между точками при отображении

(рис. 2)

увеличиваются и происходит растяжение; если | f ’(z₀)| < 1, то отображение приводит к сжатию (хотя соответствующий коэффициент все равно называют коэффициентом растяжения). Свойство данного отображения носит название свойства постоянного растяжения.

Так как производная f '(zo) не зависит от того, по какому пути точка z₀ + Δz приближается к z₀, то коэффициент растяжения одинаков во всех направлениях. Это свойство можно проиллюстрировать следующим образом. Возьмем окружность l с центром z₀ и радиусом |Δz| (т.е. приращения Δz имеют фиксированный модуль, но различные направления — рис. 2а). При отображении w = f (z) эта окружность перейдет в кривую L (рис. 2б); расстояние от точки w = f (z₀ + Δz) этой кривой до точки w₀ = f (z₀) равно

|Δw| = |w- w₀| = |f (z ₀ + Δz) – f (z₀)|.

Поскольку Δw = f ' (z₀) Δz + α (Δz) Δz, где α (Δz) → 0 при Δz → 0, то |w - w₀| = |f ' (z₀) Δz + α(Δz) Δz|. Это равенство означает, что точки кривой L будут мало отличаться от окружности |w — w₀| = |f ' (z₀)| | Δz| с центром w₀ и радиусом |f ' (z₀)| | Δz| (точнее говоря, будут отличаться от этой окружности на величину более высокого порядка малости, чем |Δz| — рис. 2б).