
LABA_5
.1.docНижегородский Государственный Технический Университет им. Р. Е. Алексеева.
Кафедра «Прикладная Математика».
Отчет: Лабораторная работа №5
«Дифференциальное уравнение».
Вариант 7
Выполнил:
Студент группы 11-КСУ-2
Кокурин М.А.
Проверил:
Преподаватель Белоцерковская И.Е.
г. Нижний Новгород 2012
Оглавление.
1 Метод Эйлера
Постановка задачи……………………………………………………………………………..3
Ручной счет……………………………………………………………………………………..3
Реализация в Microsoft Excel………………………………………………………………….4
Реализация в Mathcad………………………………………………………………………….4
Реализация в Microsoft Visual C++..…………………………………………………………..5
2 I модификация метода Эйлера
Постановка задачи……………………………………………………………………………..6
Ручной счет……………………………………………………………………………………..6
Реализация в Microsoft Excel………………………………………………………………….8
Реализация в Mathcad………………………………………………………………………….9
3 II модификация метода Эйлера
Постановка задачи…………………………………………………………………………….10
Ручной счет…………………………………………………………………………………….10
Реализация в Microsoft Excel…………………………………………………………………11
Реализация в Mathcad…………………………………………………………………………12
4 III модификация метода Эйлера
Постановка задачи…………………………………………………………………………….13
Ручной счет…………………………………………………………………………………….13
Реализация в Microsoft Excel…………………………………………………………………15
Реализация в Mathcad…………………………………………………………………………15
5 Метод Рунге-Кутта
Постановка задачи…………………………………………………………………………….16
Ручной счет……………………………………………………………………………………16
Реализация в Microsoft Excel…………………………………………………………………17
Реализация в Mathcad…………………………………………………………………………18
Реализация в Microsoft Visual C++..…………………………………………………………19
6 Вывод………………………………………………………………………………………….20
7 Список литературы…………………………………………………………………………...20
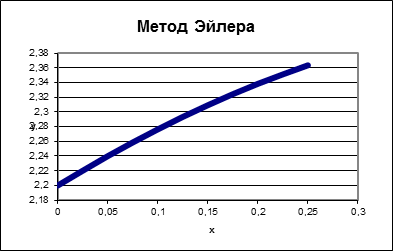
Метод Эйлера
Реализация в Microsoft Excel:
|
|
метод Эйлера |
|
|
x |
y |
z |
|
0 |
2,2 |
0,8 |
|
0,05 |
2,24 |
0,73 |
|
0,1 |
2,2765 |
0,657127 |
|
0,15 |
2,309356 |
0,581681 |
|
0,2 |
2,33844 |
0,504002 |
|
0,25 |
2,363641 |
0,424478 |

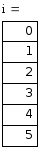
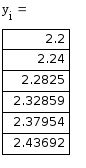
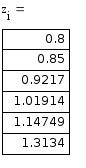
Реализация в Mathcad:
Простой
метод Эйлера
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
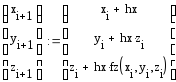
![]()

![]()
![]()
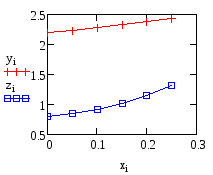
Реализация в Microsoft Visual C++:
#include <iostream>
#include <conio.h>
#include <math.h>
#include <iomanip>
#include <stdlib.h>
using namespace std;
int main()
{ double a,b,x,y[20],z[20],hx,y1[20],z1[20];
int i;
a=0;
b=0.25;
hx=0.05;
cout<<"Metod Eilera"<<endl;
i=0;
y[0]=2.2;
z[0]=0.8;
cout<<setw(10)<<"i"<<setw(10)<<"x"<<setw(10)<<"y"<<setw(10)<<"z"<<endl;
for(x=a;x<=b;x+=hx)
{cout<<setw(10)<<i<<setw(10)<<x<<setw(10)<<y[i]<<setw(10)<<z[i]<<endl;
y[i+1]=y[i]+hx*z[i];
z[i+1]=z[i]+hx*(3*z[i]+exp(5*x));
i+=1;}
getch();
return 0;}

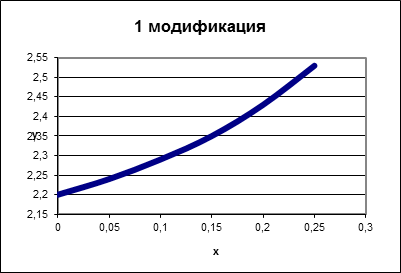
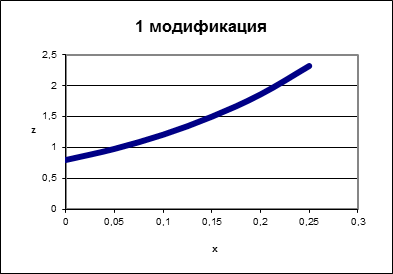
I модификация метода Эйлера
Реализация в Microsoft Excel:
|
|
1 модификация |
|
|
x |
y |
z |
|
0 |
2,2 |
0,8 |
|
0,05 |
2,24 |
0,98 |
|
0,1 |
2,29 |
1,21 |
|
0,15 |
2,35 |
1,5 |
|
0,2 |
2,43 |
1,86 |
|
0,25 |
2,53 |
2,32 |
Реализация в Mathcad:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
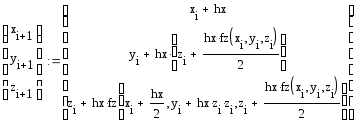
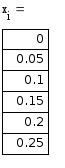
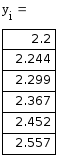
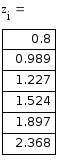
II модификация метода Эйлера
Реализация в Microsoft Excel:
|
|
2 модификация |
|
|
x |
y |
z |
|
0 |
2,2 |
0,8 |
|
0,05 |
2,24 |
1 |
|
0,1 |
2,3 |
1,26 |
|
0,15 |
2,37 |
1,59 |
|
0,2 |
2,46 |
2,01 |
|
0,25 |
2,58 |
2,55 |
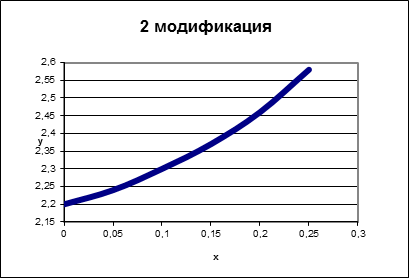

Реализация в Mathcad:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
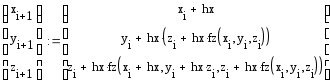
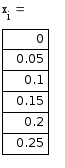
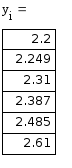
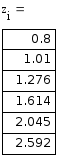
III модификация метода Эйлера
Реализация в Microsoft Excel:
|
|
3 модификация |
|
|
x |
y |
z |
|
0 |
2,2 |
0,8 |
|
0,05 |
2,24 |
0,98 |
|
0,1 |
2,29 |
1,21 |
|
0,15 |
2,35 |
1,5 |
|
0,2 |
2,43 |
1,87 |
|
0,25 |
2,53 |
2,33 |
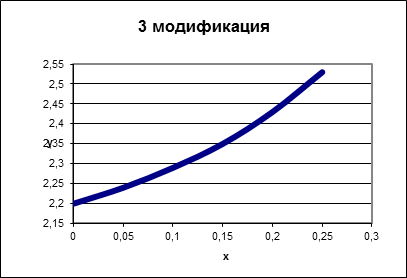
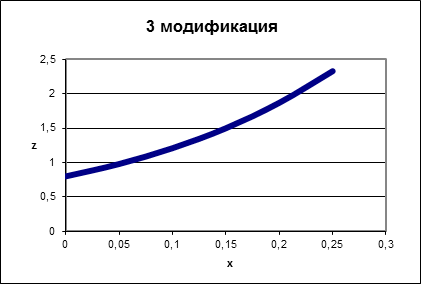
Реализация в Mathcad:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
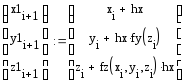
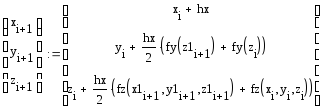
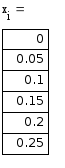
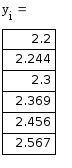
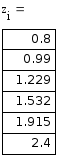
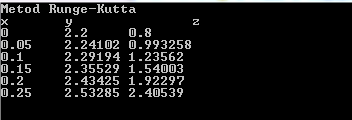
Метод Рунге-Кутта
Реализация в Microsoft Excel:
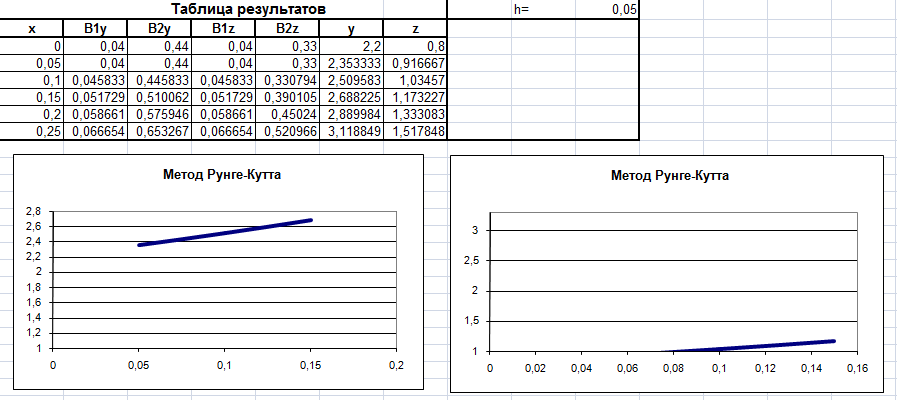
Реализация в Mathcad:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
Реализация в Microsoft Visual C++:
#include <iostream>
#include <math.h>
using namespace std;
void main()
{
double a,b,x,y[20],z[20],hx,y1[20],z1[20];
int i;
a=0;
b=0.25;
hx=0.05;
//Metod Runge-Kutta 4-ogo poryadka tochnosti
cout<<"Metod Runge-Kutta"<<endl;
double k0[11],k1[11],k2[11],k3[11],k01[11],k11[11],k21[11],k31[11];
i=0;
y[0]=2.2;
z[0]=0.8;
cout<<"x\ty\t\tz"<<endl;
for(x=a;x<=b;x+=hx)
{
cout<<x<<"\t"<<y[i]<<"\t"<<z[i]<<endl;
k0[i]=hx*z[i];
k01[i]=hx*(3*z[i]+exp(5*x));
k1[i]=hx*(z[i]+k0[i]/2);
k11[i]=hx*(3*(z[i]+k01[i])+exp(5*x));
k2[i]=hx*(z[i]+k1[i]/2);
k21[i]=hx*(3*(z[i]+k11[i])+exp(5*x));
k3[i]=hx*(z[i]+k2[i]);
k31[i]=hx*(3*(z[i]+k21[i])+exp(5*x));
y[i+1]=y[i]+(k0[i]+2*k1[i]+2*k2[i]+k3[i])/6;
z[i+1]=z[i]+(k01[i]+2*k11[i]+2*k21[i]+k31[i])/6;
i+=1;
}
char c;
cin>>c;
}
Вывод
Методом Эйлера и методом Рунге-Кутта, дают близкое друг к другу численное решение задачи Коши. Причем метод Рунге-Кутта дает более точное решение этой задачи. Он является методом четвертого порядка точности, поэтому даже с достаточно большим шагом по координате х получаем точное решение. Метод же Эйлера является методом второго порядка точности. Обычно он применяется только для прикидочных расчетов, но идеи, положенные в его основу, являются исходными для широкого класса численных методов.
