
Доказательство.
![]()
Найдем длину
![]()
![]()
![]()
Найдем длину
![]() A
A
![]()
![]() =
=![]() A
что и требовалось доказать
A
что и требовалось доказать
Ответ: а)АС=СВ
б)
![]()
в)
![]()
З
Дано:
Δ АВС;
А(0;0), В(3;1), С(1;7).
Доказать,
что Δ АВС прямоугольный.
В
А
С

Доказать, что треугольник с вершинами А(0;0), В(3;1), С(1;7) прямоугольный.
Доказательство.
![]()
2)
![]()
![]() .
.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти вектора перпендикулярны.
Значит <В=90° , следовательно треугольник АВС прямоугольный.
Что и требовалось доказать.
Задача №6.
Дано:
Δ АВС;
А(-2;1), В(4;8), С(10;6).
Доказать,
что Δ АВС тупоугольный.
А
В
С



Показать, что в треугольнике А(-2;1), В(4;8), С(10,6) один угол тупой.
Доказательство.
![]()
2)
![]()
![]() .
.
<B- тупой, так как скалярное произведение двух векторов отрицательно тогда и только тогда, когда между ними тупой угол.
Ответ: Δ АВС тупоугольный.
З
Дано:
ABCD - параллелограмм;
А(4;2), В(4;8), С(10;6).
DA и СB –
диагонали
DA
Найти:
а) D.
б) CB и DA.
в) E.
г)
![]() CB=E
CB=E![]() CAB.
CAB.
E D
С
В
А
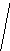




Даны три вершины параллелограмма А(4;2), В(5;7), С(-3;4)
а) Найти координаты четвертой вершины D;
б) Длины диагоналей AD и CB;
в) Точку пересечения диагоналей E;
г) Угол при вершине А.
Решение.
а) Известно, что диагонали параллелограмма
в точке пересечения делятся пополам.
Поэтому координаты точки E - пересечения
диагоналей - найдем как координаты
середины отрезка AC. Обозначая их через
![]() получим,
что
получим,
что
![]() .
.
![]()
E(1; 5,5)
Зная координаты точки Е – середины диагонали AD и координаты одного из его концов А(4; 2), по формулам
![]()
![]()
где
х=1,
![]() =4,
у=5,5,
=4,
у=5,5,
![]() =2,
получим
=2,
получим
![]() .
.
![]() =-2
=-2
![]()
![]() =9
=9
D(-2;9).
б)
![]()
![]()
в) Найдем уравнения прямых содержащие
диагонали параллелограмма АD
и ВС по формуле
![]() .
.
AD:
![]() .
.
![]() 7х-28=-6у+12,
7х-28=-6у+12,
6у+7х-40=0.
ВС:
![]()
![]() -3х+15=-8у+56,
-3х+15=-8у+56,
8у-3х-41=0.
Найдем точку пересечения прямых АD и ВС:
![]() .
.
![]() =6(-3)-7
=6(-3)-7![]() 8=-18-56=-74;
8=-18-56=-74;
![]() =40
=40![]() =-120-287=-407;
=-120-287=-407;
![]() =40
=40![]()
![]() 320-246=74;
320-246=74;
![]() .
.
![]()
E(-1; 5,5) - точка пересечения диагоналей
г) Найдем уравнение прямых АВ и АС по формуле
![]() .
.
представим уравнение в виде у=кх+в
АВ:
![]()
![]() 5х-20=у-2,
5х-20=у-2,
у=5х-18,
![]() .
.
АС:
![]()
![]() 2х-8=-7у+14,
2х-8=-7у+14,
7у=-2х+22,
![]() ,
,
![]() .
.
 .
.
<A=arctg![]()
Ответ: а) D(-2;9); б) BC=![]() ;
АD=
;
АD=![]() ;
в) Е(-1; 5,5); г)
;
в) Е(-1; 5,5); г)
![]() САВ=arctg
САВ=arctg![]()
Задача №8.
С Дано:
AB: х+2у=0,
BC: х+4у-6=0;
AC: х-4у-6=0.
Найти
А
В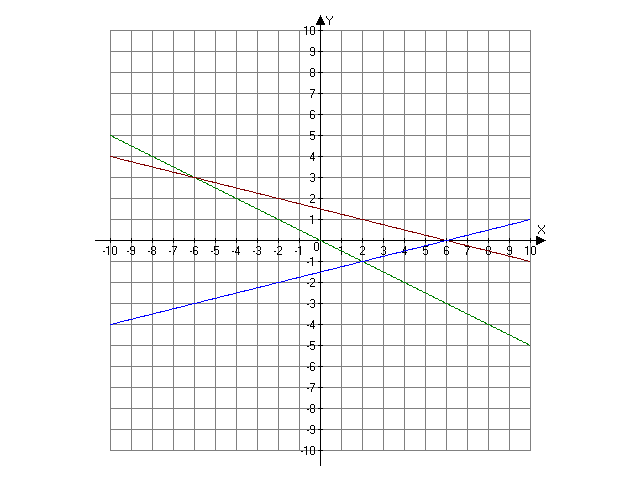
![]() ВAС,
ВAС,
![]() АBС,
АBС,
![]() ВCА.
ВCА.
Найти внутренние углы треугольника, стороны которого заданы уравнениями х+2у=0, х+4у-6=0; х-4у-6=0.
Решение
x+2у=0, х+4у-6=0, х-4у-6=0 распишем эти уравнения по формуле у=кх+в
AB:
х+2у=0,
2у=-х,
![]() .
.
![]() ВС:
ВС:
х+4у-6=0,
4у=-х+6,
![]() .
.
![]()
AC:
х-4у-6=0,
4у=х-6,
![]()
![]()

![]()
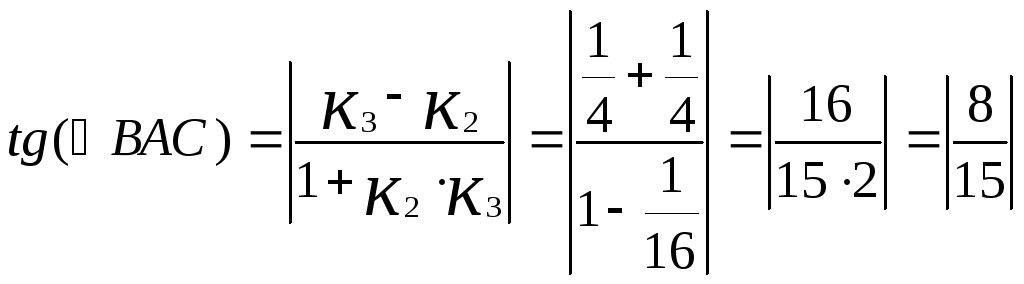
![]()
![]() BAC=180°-28°-12°30'=139°30'.
BAC=180°-28°-12°30'=139°30'.
Ответ:
![]() ABC=
12°30';
ABC=
12°30';
![]() BAC=28°;
BAC=28°;
![]() BCA=139°30'.
BCA=139°30'.
Задача №9
Вычислить координаты вершин ромба, если известны уравнения двух его сторон: x+2y=4 и х+2у=10 и уравнение одной из его диагоналей у=х+2
Дано:
Найти: А,В,С и D.
