
Задача №1
Найти координаты вершин треугольника, если стороны заданы уравнениями:
x - 2y + 3 = 0; 2x - y – 3 = 0; x + y – 3 = 0;
Дано: АВ: х-2у+3=0, АС: 2х-у-3=0, ВС: х+у-3=0
Найти: А,В и С.
Решение.
Найдем вершины треугольника АВС, как точки пересечения сторон треугольника.
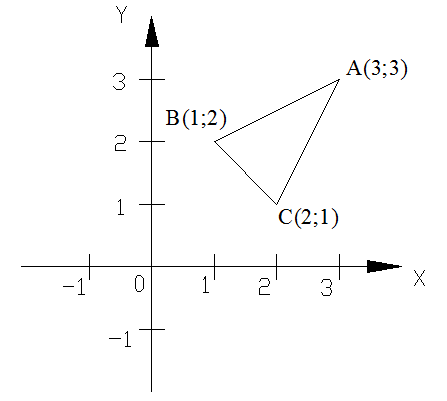
т.А:
![]()
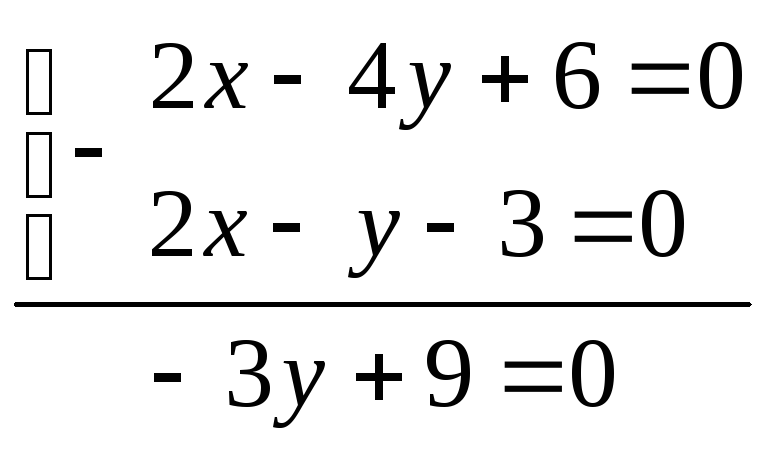
3у=-9 у=3, x-2*3+3=0, у=3, х=3
имеем: A(3;3)
т. В:
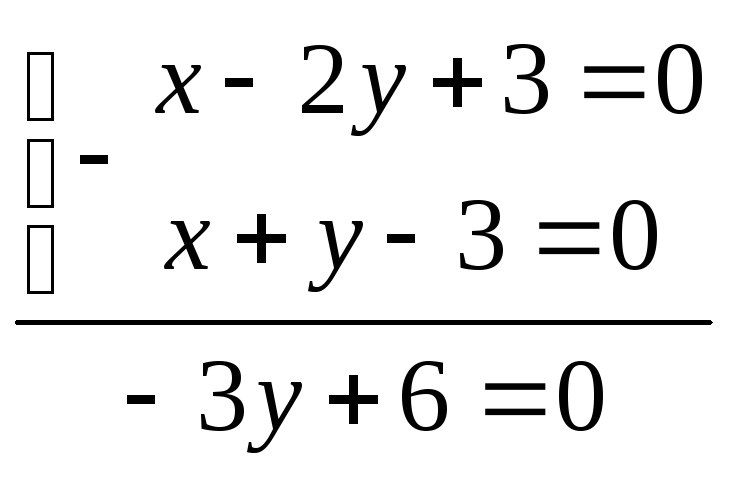 .
.
![]() х-2*2+3=0,
у=2, х=1
х-2*2+3=0,
у=2, х=1
имеем: т. B(1;2)
т.С :
 .
.
3х=6 х=2, 2+y-3=0, х=3, y=1
имеем: т. C(2;1)
Ответ: координаты вершин треугольника: А (3;3); В(1;2); С(2;1).
Задача №2
Даны вершины треугольника:![]() ;2);
;2);
![]() ;3);
;3);
![]() ;1).
;1).
Написать уравнение высоты, опущенной
из точки
![]()
Решение
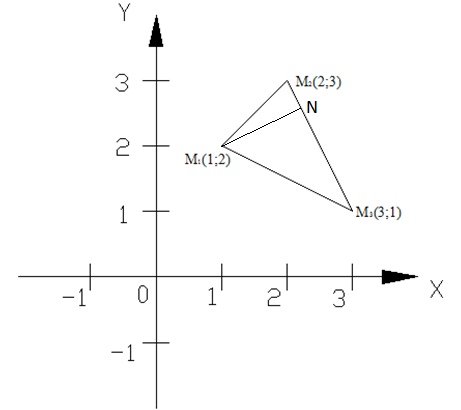
Дано:
![]() (1;2);
(1;2);
![]() (2;3);
(2;3);
![]() (3;1)
- вершины треугольника
(3;1)
- вершины треугольника
![]()
Решение: проведем из точки
![]() высоту
к стороне
высоту
к стороне
![]() запишем уравнение стороны
запишем уравнение стороны![]()
![]()
откуда имеем
-2х+4-у+2=0,
у+2х-6=0, у = -2х+6, т.е. угловой коэффициент
прямой k= -2. Тогда, угловой
коэффициент перпендикулярной прямой
(высоты
![]() )
будет
)
будет
![]() .
Найдем уравнение высоты, как уравнение
прямой, проходящей через одну точку:
y-y1
=k(x-x1),
Где x1 и y1
– координаты точки
.
Найдем уравнение высоты, как уравнение
прямой, проходящей через одну точку:
y-y1
=k(x-x1),
Где x1 и y1
– координаты точки ![]() .
.
y-2=![]() (x-1), откуда имеем 2y-x-3=0
(x-1), откуда имеем 2y-x-3=0
![]() .
.
![]() откуда, преобразовав, получим
откуда, преобразовав, получим
2у-х-3=0
Ответ: уравнение высоты 2у-х-3=0
Задача №3.
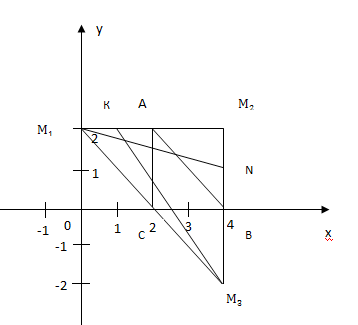
Даны вершины треугольника M1M2M3: М1(-3;0), M2(2;5), M3(3;2).
а) Найти периметр треугольника, вершинами которого служат середины сторон.
б) Найти периметр треугольника, вершинами которого служат основания высот, проведенных из вершин M1 M2 M3 к противоположным сторонам.
в) Найти периметр треугольника, вершинами которого служат основания биссектрис, проведенных из вершин M1 M2 M3 к противоположным сторонам.
Решение.
а) Построение:
К, Е, F – середины соответствующих сторон М1М3, М1М2, М2М3.
F E K
M1
M2
M3






К – середина М1М3, тогда координаты середины стороны будут:
![]()
![]() Тогда К(0;1).
Тогда К(0;1).
Е – середина М1М2, тогда координаты середины стороны будут:
![]()
![]()
тогда Е(-0,5; 2,5).
F – середина М2М3, тогда координаты середины стороны будут:
![]() .
.
![]()
тогда F(2,5; 3,5).
KF=![]()
Аналогично: EF=![]() ;
EK=
;
EK=![]() .
Тогда периметр
треугольника будет:
.
Тогда периметр
треугольника будет:![]()
б)
M1
M2
M3=N=M K


 Где
М1 ?
Где
М1 ?
Покажем, что треугольник прямоугольный и его три высоты не могут составить замкнутую фигуру.
Найдем уравнение стороны М1М2:
![]() откуда имеем
откуда имеем
5x+15=5y; y=x+3. Хорошо видно, что угловой коэффициент этой прямой k1=1, а
т. к. высота М3К перпендикулярна
стороне М1М2, то k2![]()
Используя уравнение прямой через точку: у-y1=k(x-x1) имеем
M3K:
y-2=-1(x-3), y-2=-x+3 откуда получаем y+x-5=0.
Уравнение пучка прямых:
![]() .
.
2y=8,
y=4,
то x=1, тогда М3К![]() М1М2=К(1;4).
М1М2=К(1;4).
Найдем уравнение стороны М2М3:
![]() .
.
-3x+6=y-5, y=-3x+11, откуда видно что угловой коэффициент этой прямой k1=-3,
т. к. М1N
перпендикуляреныМ2М3, k2![]()
тогда уравнение стороны М2М3
будет
![]() ,
3y-x-3=0
,
3y-x-3=0
Уравнение пучка прямых:
![]() .
.
у=11-3x, 33-9x-x-3=0. x=3 y=2, то x=3,
тогда
М1N![]() М2М3=N(3;2).
М2М3=N(3;2).
Найдем уравнение стороны М1М3:
![]() .
.
2x+6=6y, 3x-x-3=0,
y=![]() x+1,
k1=
x+1,
k1=![]() ,
то k2
,
то k2![]() т. к. М2M перпендикулярна
М1М3, k2=
т. к. М2M перпендикулярна
М1М3, k2=![]() .
Найдем уравнение
стороны М1N:
.
Найдем уравнение
стороны М1N:
y-5=-3(x-2), y-5=-3x+6, y+3x-11=0.
Уравнение пучка прямых:
![]() .
.
y=2, то x=3,
тогда М2M![]() М1М3=N(3;2).
М1М3=N(3;2).
Имеем:
KN=![]() ;
КM=
;
КM=![]() ;
NM=0; т.е. мы доказали, что
;
NM=0; т.е. мы доказали, что
ΔКNM не существует
в)Построение: М1А, М2В и М3С – биссектрисы углов при вершинах М1М2 М3
A C B
M3
M2
M1



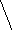

Найти периметр треугольника АВС
1)
![]()
![]() .
.
![]() (у-х-3)=3у-х-3;
(у-х-3)=3у-х-3;
![]() у-
у-![]() х-3
х-3![]() =3у-х-3;
=3у-х-3;
у(![]() -3)+х(-
-3)+х(-![]() +1)+(3-3
+1)+(3-3![]() )=0
- уравнение биссектрисы
)=0
- уравнение биссектрисы
![]()
2)![]()
![]() .
.
![]() (у-х-3)=у+3х+11;
(у-х-3)=у+3х+11;
![]() у-
у-![]() х-3
х-3![]() =у+3х+11;
=у+3х+11;
у(![]() -1)+х(-
-1)+х(-![]() -3)+(-3
-3)+(-3![]() +11)=0
- уравнение биссектрисы
+11)=0
- уравнение биссектрисы
![]()
3)
![]()
![]() .
.
3у-х-3=у+3х-11;
2у-4х+8=0 - уравнение
биссектрисы
![]()
Найдем основания биссектрис, как точки пересечения сторон треугольника и с ответствующей биссектрисы :
1)
![]()
![]() =-4
=-4![]() ;
;
![]() =-20
=-20![]() +20;
+20;
![]() =
=![]()
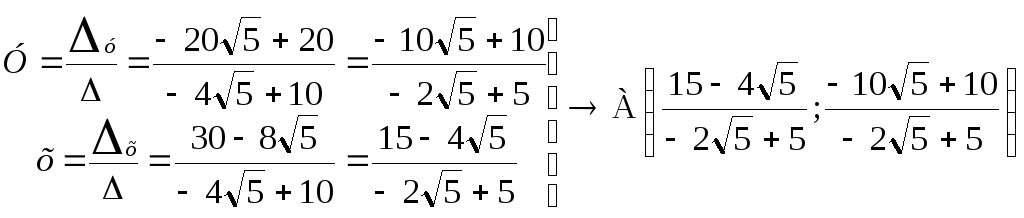 .
.
2)
![]()
![]()
![]() ;
;
![]() ;
;
![]() .
.
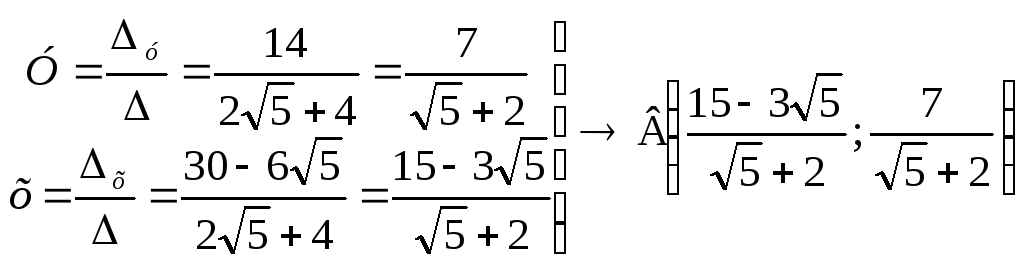 .
3)
.
3)
![]()
![]() .
.
![]()
![]()
у =10, х=7 Следовательно С(7,0)
Найдем
![]()
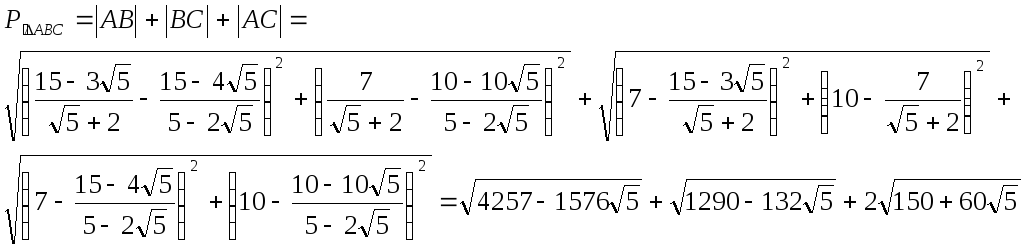
Задача №4
Даны вершины равнобедренного треугольника
![]()
а)Доказать, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника.
б) Доказать, что биссектриса, проведенная из вершины при основании равны.
в) Медианы, проведенные из вершин при основании равны.
а)Дано: ΔАВС
Доказать, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника.
Доказательство.
Найдем середины сторон треугольника
1) Найдём середину отрезка A![]()
![]()
![]()
![]() А(2;
2)
А(2;
2)
2) Найдём середину отрезка B![]()
![]()
![]()
В(4;0)
3) Найдём середину отрезка C(![]()
![]()
![]()
С(2;0)
4)
![]()
![]() АС=CB
АС=CB
![]() треугольник
АВС - равнобедренный, что и
требовалось доказать
треугольник
АВС - равнобедренный, что и
требовалось доказать
б)Дано![]() :
:
Доказать, что биссектриса, проведенная из вершины при основании равны.
Доказательство.
1)
![]()
Найдём каноническое уравнение 2-ух точек M3, M1
![]()
![]()
![]()
4-x=y+2,
x+y-2=0
![]() x-4=0
x-4=0
Найдём каноническое уравнение 2-ух точек
![]()
![]()
![]()
y+x-3=![]()
у+(1-![]()
![]()
у=2,
y-2=0
![]() .
.
Составим систему уравнения из
![]()
![]()
![]()
![]()
![]()
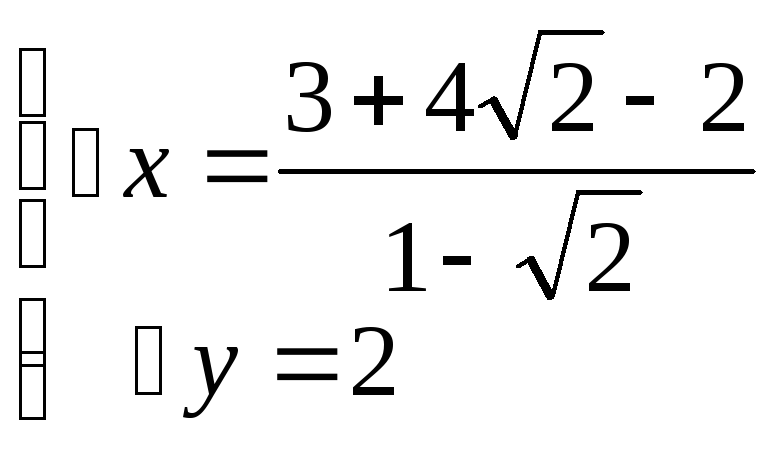
![]() K
K![]()
Найдем длину![]() .
.
![]()
2) Найдём каноническое уравнение 2-ух
точек
![]()
![]()
![]()
у![]()
![]()
![]()
Составим систему уравнения из
![]()
![]()
![]()
![]()
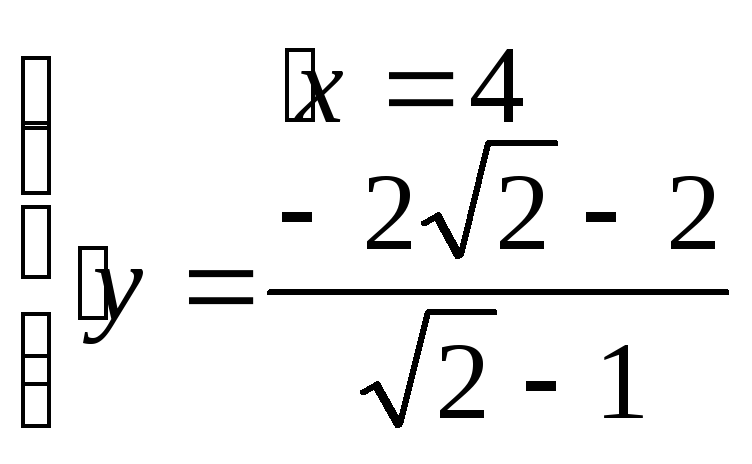
![]()
Найдем длину
![]()
![]()
![]() что и требовалось доказать
что и требовалось доказать
в)Дано: ΔАВС и
![]() оказать,
что медианы, проведенные из вершин при
основании равны.
оказать,
что медианы, проведенные из вершин при
основании равны.
