НИРС_Хитева

ОТЗЫВ

о научно-исследовательской работе студента

студенткой 4 курса дневной формы обучения (группа 10-ПМ)

специальности 010501 «Прикладная математика и информатика» института радиоэлектроники и информационных технологий

Нижегородского государственного технического университета им Р.Е.Алексеева

Хитевой Дарьей Вячеславовной

(ФИО полностью)

1. Общие сведения

Место прохождения НИРС:

НГТУ им Р.Е. Алексеева, каф. «Прикладная математика», г. Н. Новгород

(полное наименование организации, город)

2. Основные формы и виды работы студента.

В соответствии с планом прохождения НИРС.

3. Общая оценка НИРС.

По итогам НИРС считаю, что

Хитева Д.В. заслуживает оценки

Алексеенко С.Н.

(подпись, дата, ФИО)

Научный руководитель:

Руководитель НИРС от организации:

Профессор кафедры «Прикладная математика» Куркин А.А.
(полное наименование должности, подразделения, подпись, дата)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ

ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«Нижегородский государственный технический университет им. Р.Е. Алексеева» (НГТУ)

ИНСТИТУТ РАДИОЭЛЕКТРОНИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра «Прикладная математика»

НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА СТУДЕНТА

Тема: «Применение метода дополнительного аргумента к исследованию разрешимости и построению численных решений лиминального диссипативного дифференциального уравнения плотности дислокаций»

Выполнила студентка

группы 10-ПМ:

Хитева Д.В.

Проверил:

Алексеенко С.Н.

(подпись, ФИО)

Оценка:

г. Нижний Новгород

2014 год

Содержание

1. Введение

2. Цели:

3. Задачи:

4. Актуальность

5. Теоретическая часть

6. Реализация:

7. Результат работы:

8. Список литературы

Введение

Дифференциальные уравнения в частных производных первого порядка играют важную роль практически во всех направлениях науки. Это в большей степени объясняется потребностями задач прикладного характера. Многие задачи физики, математической физики, гидродинамики, механики, теории оптимального управления и т.д. приводят именно к уравнениям в частных производных первого порядка.

Существует большое количество различных методов для исследования разрешимости нелинейных дифференциальных уравнений в частных производных первого порядка. Но каждый из известных методов хорошо применим только к определенному классу уравнений. Рассматривается еще один способ исследования разрешимости нелинейных дифференциальных уравнений в частных производных первого порядка - метод дополнительного аргумента. Он не заменяет собой другие известные методы, а дополняет их. Применение этого метода позволяет во многих случаях более эффективно и конкретно определить условия разрешимости уравнений.

Цели:

Целью данной работы является исследование разрешимости и построение численных решений лиминального диссипативного дифференциального уравнения плотности дислокаций с помощью метода дополнительного аргумента.

Задачи:

С применением метода дополнительного аргумента определить условия локальной разрешимости заданного уравнения.

Актуальность

В данной работе впервые выведено дифференциальное уравнение в частных производных первого порядка с квадратичной нелинейностью и коэффициентом перед квадратом первой производной, который может обращаться в нуль. Это уравнение было названо лиминальным.

Теоретическая часть

……

В результате приходим к нелинейному дифференциальному уравнению

,

…..

Составим расширенную характеристическую систему с дополнительным аргументом

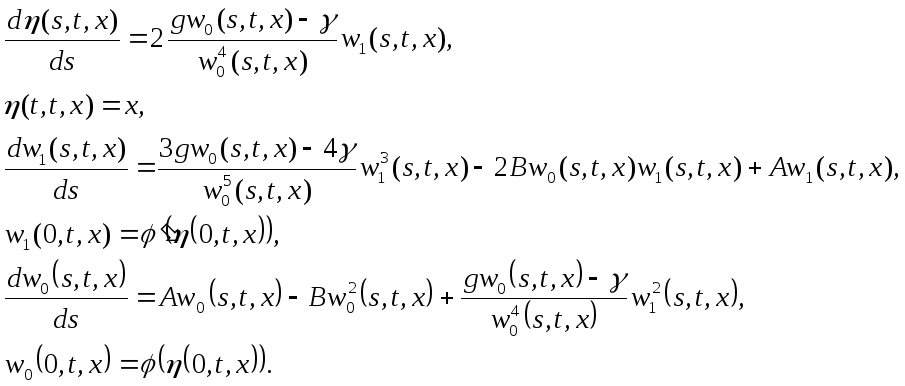
Получим систему интегральных уравнений

Запишем последовательные приближения

Оценивая правые части последовательных приближений, приходим к выводу, что при

,

где

,

,

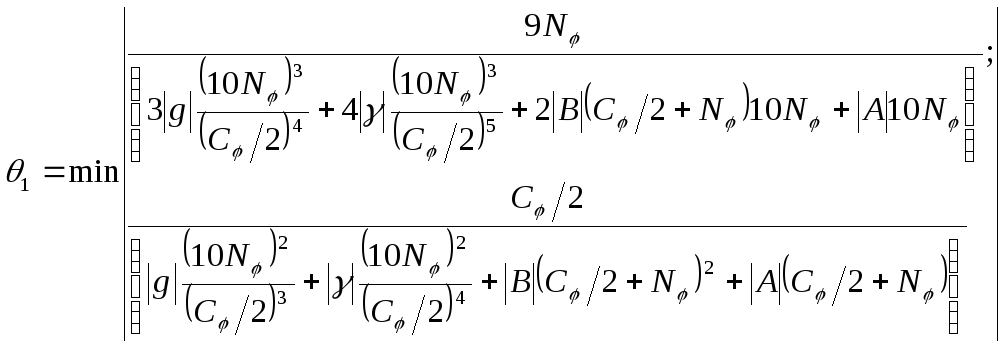выполняются неравенства

.

Рассмотрим вектор 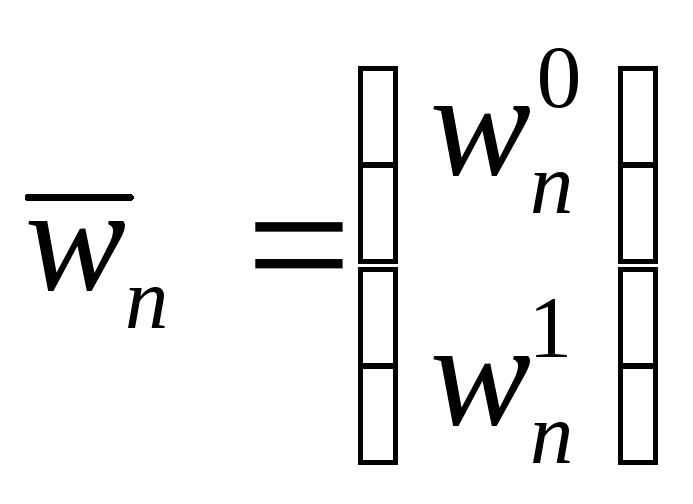. Доказывается, что последовательные приближения сходятся по норме к вектору . За норму вектора положим сумму норм и :

.

Тогда получаем:

,

где

,

, ,

, ,

,

,

,

.

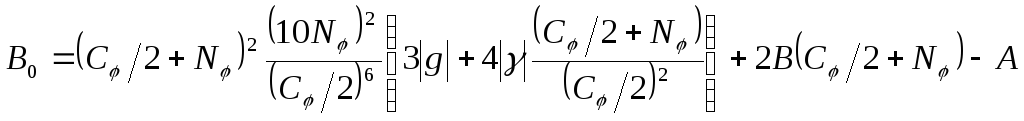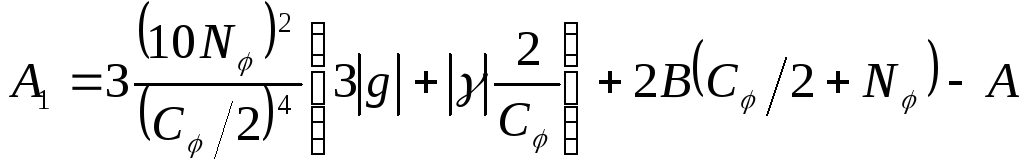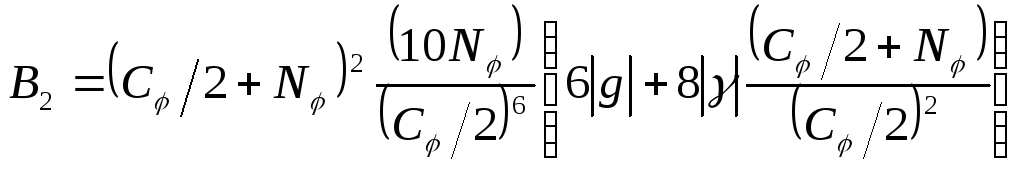Получим, что ряды и сходятся к функциям и по норме.

Единственность следует из того факта, что для разности двух возможных решений будет выполняться неравенство вида

,

где .

Далее докажем существование, непрерывность и ограниченность частных производных функций и . Запишем последовательные приближения:

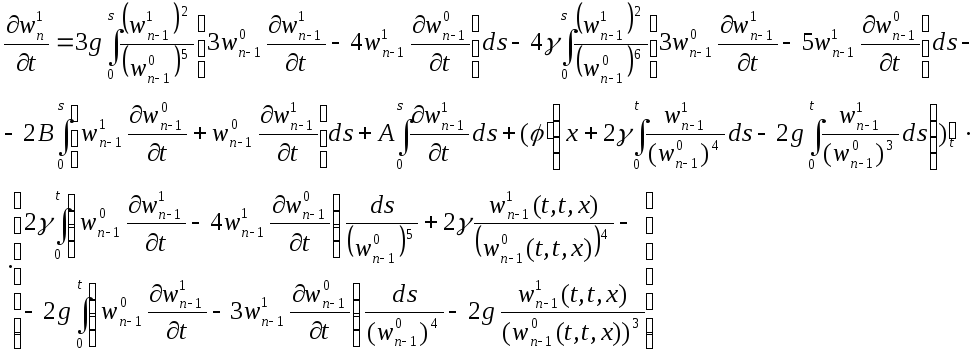
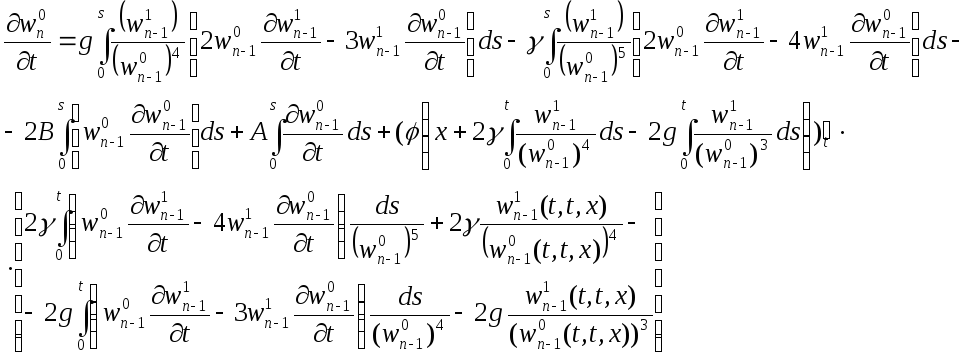
Снова введем в рассмотрение вектор . За его норму положим сумму норм и :

.

Тогда получаем:

,

где

,

.

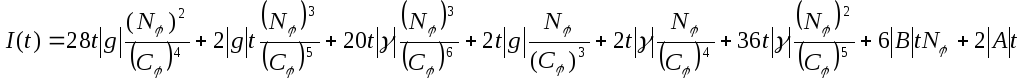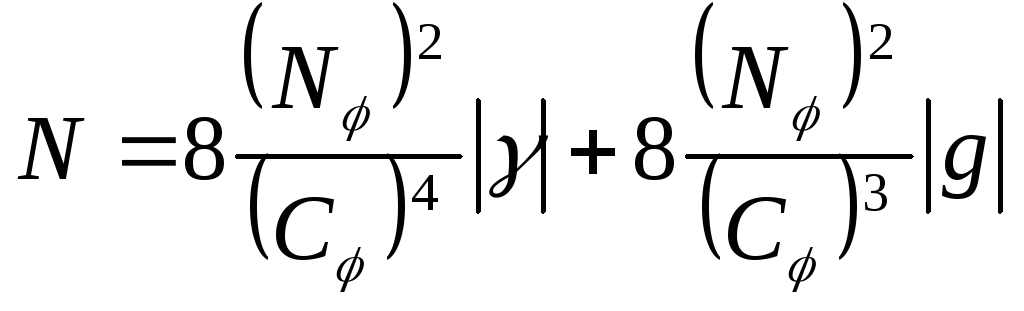Показывается, что последовательность ограничена по норме. Следовательно, ограничены по норме и последовательности , .

Для доказательства сходимости рассмотрим линейные интегральные уравнения относительно неизвестных функций и .

Реализация:

В процессе прохождения научно-исследовательской практики на кафедре «Прикладная математика» определила условия локальной разрешимости нового вида нелинейного дифференциального уравнения: были построены последовательные приближения, доказана их ограниченность и сходимость. Так же с помощью последовательных приближений была доказана ограниченность и сходимость производных первого порядка.

Для частного случая лиминального уравнения проводится численная реализация, которая на данный момент находится в стадии разработки.

Результат работы:

Задание, поставленное на практику, было реализовано студенткой Хитевой Дарьей Вячеславовной в полном объеме.

В дальнейшем планируется продолжить исследования лиминального уравнения, его нелокальной разрешимости.

Список использованной литературы

(сам заголовок должен быть по центру, а перечисление «выравнивание по левому краю») (не менее 10 ссылок)