2.4. Активная, реактивная и полная мощности. Баланс мощностей

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.       Пусть напряжение и ток являются синусоидальными функциями времени:

.

 Получим выражение для мгновенной мощности:  (2.29)

Из (2.29) следует, мгновенная мощность изменяется с частотой , в два раза превышающей частоту тока и напряжения.

  Среднее значение мгновенной мощности за период T называют активной мощностью и обозначают буквой P:

(2.30)

При выводе (2.30) учтено равенство

Учитывая из треугольника сопротивлений (рис.2.15) соотношение и из треугольника проводимостей (рис.2.16), получаем из (2.30) следующие выражения для активной мощности:

(2.31)

Активная мощность измеряется в ваттах (Вт) и характеризует необратимое преобразование электрической энергии, которая выделяется в виде теплоты на участках цепи в активных сопротивлениях. В электрических двигателях потребляемая из сети активная мощность преобразуется в механическую мощность (за вычетом потерь в процессе преобразования) и является их основной характеристикой.

Множитель называется коэффициентом мощности. Коэффициент  мощности  является одной из важнейших характеристик электротехнических устройств, и повышение его до предельного значенияостается одной из основных задач энергосбережения.

Рассмотрим идеальные реактивные элементы (индуктивность и емкость). Активная мощность в этих элементах равна нулю, так как напряжение и ток в индуктивности или емкости различаются по фазе на 90^o и

В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый  процесс в  виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

 Преобразуем выражение (2.29) для мгновенной мощности:

где - мгновенная мощность в активном сопротивлении;

- мгновенная мощность в реактивном элементе (в индуктивности или в емкости).

Максимальное или амплитудное значение мощности p₂ называется реактивной мощностью:

Q =(2.32)

где x, b – соответственно реактивные сопротивление и проводимость. Реактивная мощность измеряется в вольт-амперах реактивных (ВАр) и расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Амплитудное значение суммарной мощности p = p₁ + p₂ называется полной мощностью. Полная  мощность,  измеряемая в вольт-амперах (ВА), равна произведению действующих значений напряжения и тока:

. (2.33)

Возьмем треугольник сопротивлений (рис.2.15) и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 2.17).

Рис. 2.17

Из треугольника мощностей получим соотношения между мощностями P, Q, S:

Q =,   . (2.34)

При расчете электрических цепей комплексным методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока.     Для цепи, имеющей активно-индуктивный характер, ток по фазе отстает от напряжения на угол

,

где    - комплекс напряжения;- комплекс тока;- сопряженный комплекс тока;- сдвиг по фазе между напряжением и током.           Вещественной частью полной комплексной мощности является активная мощность, мнимой частью комплексной мощности - реактивная мощность:

Q = . (2.35)

     Для цепи, имеющей активно-емкостной характер, ток по фазе опережает напряжение .

Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.

При выводе полученных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если к зажимам цепи присоединен идеальный источник синусоидальной ЭДС с действующим значением E, то выражения (2.31)-(2.33), (2.35) для источника имеют следующий вид:

Q=

; Q = . (2.36)

Из закона сохранения энергии следует, что для электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками.

Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей. Определим комплексные мощности для схемы (рис.2.7), содержащей идеальный источник синусоидальной ЭДС, последовательно соединенные активные и реактивные сопротивления приемника.

Запишем уравнение по второму закону Кирхгофа, умножим левую и правую части уравнения на сопряженный комплекс тока и учтем свойства произведения комплексно сопряженных чисел:

, ,

где   - результирующее реактивное сопротивление.

,

где    - полная комплексная, активная и реактивная мощности источника питания.

,

 где активная и реактивная мощности, потребляемые элементами схемы.

Получим уравнение для комплексных мощностей источника и приемника:

     (2.37)

Равенство (2.37) выражает баланс комплексных мощностей источника и приемника. При равенстве комплексных чисел равны по отдельности их вещественные и мнимые части, следовательно, уравнение (2.37) можно записать в следующей форме:

 .    (2.38)

Из следует (2.38), что для электрической цепи соблюдается закон баланса реактивных мощностей: реактивная мощность, отдаваемая источниками, равна реактивной мощности, потребляемой всеми приемниками.

Рассмотрим условие передачи источником максимальной мощности при заданном коэффициенте мощности приемника.

В схеме на рис. 2.18 обозначены :  - полное, активное и реактивное сопротивления источника ЭДС,- полное, активное и реактивное сопротивления нагрузки.

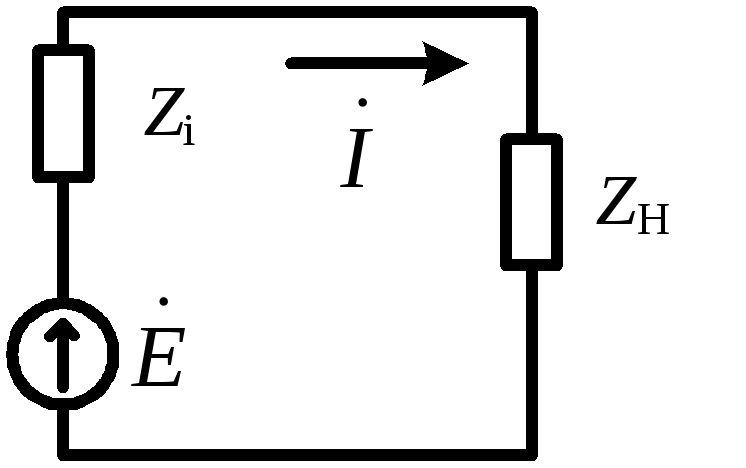
Рис. 2.18

 Активная мощность может выделяться только в активных сопротивлениях цепи переменного тока. Активная мощность, выделяемая в нагрузке,

.    (2.39)

Активная мощность, развиваемая генератором . Коэффициент полезного действия (КПД) для данной схемы:

.

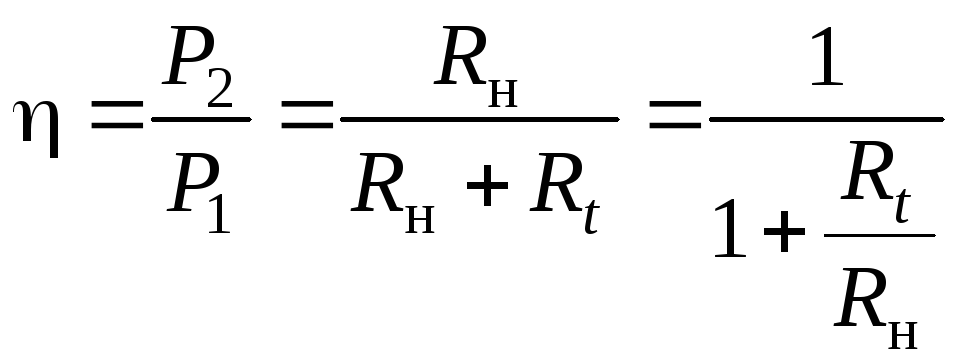Из (2.39) видно, что выделяемая в нагрузке мощность будет максимальной, когда знаменатель минимален. Последнее имеет место при , т.е. при. Это означает, что реактивные сопротивления источника и нагрузки должны быть одинаковы по модулю и иметь разнородный характер. При индуктивном характере реактивного сопротивления источника реактивное сопротивление нагрузки должно быть емкостным, и наоборот:

. (2.40)

   Установим условие,  при котором  от источника к нагрузке будет передаваться наибольшая мощность:

.

отсюда .

 От источника к нагрузке передается наибольшая мощность, когда

;      .  (2.41)

     Величина наибольшей мощности

. (2.42)

 Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений согласно равенствам (2.41) - согласованием нагрузки с источником.

   В согласованном режиме величина КПД составляет:

.

Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке.