Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

shpory_chast_1_3

.rtf

Скачиваний:

Добавлен:

28.03.2015

Размер:

21.12 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

1.Понятие матрицы

Матрицей размерности (mn) называется прямоугольная таблица чисел или функций, содержащая m строк и n столбцов. Здесь m и n - натуральные числа.

Если m=n, то матрица называется квадратной порядка n.

Размерность матрицы А обозначают символом dim A=(mn). Читается: «размерность матрицы А равна m на n».

В дальнейшем матрицу А будем записывать в виде

или

Для обозначения матриц используют прописные буквы А, В, С, , либо символы или , (i = 1, 2, , m, j = 1, 2, , n), либо A=, причем, элемент находится на пересечении i-ой строки и j-ого столбца матрицы. Числа или функции называются элементами матрицы А.

Если все элементы матрицы А равны 0, то есть =0, то матрица А называется нулевой матрицей и обозначается символом .

Элементы , , , квадратной матрицы А образуют главную диагональ этой матрицы.

Квадратная матрица А называется треугольной, если =0 при i>j или j>i (верхняя-числа НАД 0 или нижняя-числа ПОД 0).

В множестве матриц вводится понятие равенства матриц: две матрицы одинаковой размерности называются равными, если их соответствующие элементы равны.

Пусть

, , ,

тогда .

2. Операции над матрицами

А. Сумма. Суммой двух матриц А и В одинаковой размерности называется матрица С той же размерности, элементы которой равны сумме соответствующих элементов слагаемых, т.е. .

Для обозначения операции сложения матриц используют запись С=А+В.

Например, если

и , то .

Операция сложения матриц обладает двумя свойствами:

1.А+В = В+А 2.(А+В)+С = А+(В+С).

Б. Умножение на число. Произведением матрицы А размерности (mn) на вещественное число называется матрица С той же размерности, элементы которой равны произведению числа на соответствующие элементы матрицы А, т.е. .

Для обозначения этой операции используют запись С= А.

Операция умножения матрицы на число обладает свойствами:

(А) = ()А, 2.(А+В) = А+В,

3.(+)А = А+А.

Замечание. Операция вычитания матриц А и В вводится как сложение матриц А и (-1)В. Деление матрицы А на число 0 вводится как умножение А на число .

Например, если

, то и .

1.Понятие матрицы

Если m=n, то матрица называется квадратной порядка n.

Размерность матрицы А обозначают символом dim A=(mn). Читается: «размерность матрицы А равна m на n».

В дальнейшем матрицу А будем записывать в виде

или

Элементы , , , квадратной матрицы А образуют главную диагональ этой матрицы.

Квадратная матрица А называется треугольной, если =0 при i>j или j>i (верхняя-числа НАД 0 или нижняя-числа ПОД 0).

Пусть

, , ,

тогда .

2.произведение матриц

В. Умножение матриц. Произведением матрицы размерности (mn) на матрицу размерности (np) называется матрица размерности (mp), элементы которой определяются по формуле: (1)

Произведение матриц А и В обозначается как С=АВ.

Следует отметить, что не всякие матрицы можно перемножать, т.к. для выполнения операции умножения матриц необходимо и достаточно чтобы число столбцов первой матрицы было равно числу строк второй матрицы.

Возможно существует произведение АВ , но не существует произведение ВА. Может также случиться, что оба произведения АВ и ВА существуют, но не являются равными. Следовательно, в общем случае операция умножения матриц не обладает свойством коммутативности, т.е. АВ ВА.

Заметим далее, что формула (1) означает, что элемент _, стоящий на пересечении i-ой строки и j-ого столбца матрицы С=АВ, равен сумме попарных произведений соответствующих элементов i-ой строки матрицы А и j-ого столбца матрицы В.

Например, если

и ,то

1. Понятие определителя.

Далее введем операцию соответствия каждой квадратной матрице некоторого вещественного числа, называемого определителем или детерминантом этой матрицы и обозначаемого символом det A или .

Понятие определителя матрицы А порядка n введем индуктивно. Если порядок матрицы А равен 1, то она состоит из одного элемента . В этом случае определителем матрицы А будем называть число (или функцию) ,

т.е. det A=.

Если порядок матрицы А равен 2, то определителем ее будем называть выражение det A , определяемое по формуле:

(2).

Если порядок матрицы А равен 3, то определителем ее будем называть выражение

Заметим, что каждое слагаемое здесь представляет собой произведение трех элементов матрицы, взятых из каждого столбца и каждой строки. Причем знаки слагаемых выбираются следующим образом: «плюс», если произведение трех элементов составлено по схеме «а», и «минус», если - по схеме «б».

«а», «б»

Предположим далее, что понятие определителя матрицы порядка (n-1) введено, и перейдем к формированию понятия определителя порядка n.

Для этого введем несколько новых определений.

Минором элемента матрицы А порядка n будем называть определитель матрицы порядка (n-1), полученной из матрицы A вычеркиванием в ней i-ой строки и j-ого столбца. Этот минор будем обозначать символом .

Алгебраическим дополнением элемента матрицы А будем называть выражение , обозначаемое символом , т.е. =.

Основное понятие.

Определителем матрицы А порядка n называется число, равное и обозначаемое символом или det A, т.е.

det A= (3)

Формула (3) представляет собой закон разложения определителя порядка n по элементам первой строки.

Покажем, что вычисление определителя второго порядка по формуле (3) совпадает с правилом вычисления - (2).

Действительно, если дана матрица

А=, то , . Поэтому формула (3) дает

Что и требовалось доказать.

1. Понятие определителя.

т.е. det A=.

Если порядок матрицы А равен 2, то определителем ее будем называть выражение det A , определяемое по формуле:

(2).

Если порядок матрицы А равен 3, то определителем ее будем называть выражение

«а», «б»

Для этого введем несколько новых определений.

Алгебраическим дополнением элемента матрицы А будем называть выражение , обозначаемое символом , т.е. =.

Основное понятие.

Определителем матрицы А порядка n называется число, равное и обозначаемое символом или det A, т.е.

det A= (3)

Формула (3) представляет собой закон разложения определителя порядка n по элементам первой строки.

Покажем, что вычисление определителя второго порядка по формуле (3) совпадает с правилом вычисления - (2).

Действительно, если дана матрица

А=, то , . Поэтому формула (3) дает

Что и требовалось доказать.

2.Свойства определителей.

а)Для всякой матрицы порядка n имеет место формула разложения определителя ее по первому столбцу:

det A=

б) Определитель транспонированной матрицы (квадратной) равен определителю исходной матрицы, т.е.

в) При перестановке местами двух строк или двух столбцов матрицы определитель ее сохраняет абсолютную величину, но меняет знак на противоположный.

г) Если s-ый столбец квадратной матрицы A является линейной комбинацией столбцов (), (), т.е.

; k=1,2,, n ; b,cR,

то ,

где и - матрицы полученные из А заменой s-ого столбца ее на столбцы () и () соответственно.

д) Определитель матрицы A равен нулю, если:

Матрица A имеет одинаковые строки или столбцы;
Строка (столбец) матрицы A является линейной комбинацией других строк (столбцов);
Матрица A имеет нулевую строку или столбец.

е) Сумма произведений элементов какой-либо строки (столбца) матрицы на их алгебраические дополнения равна определителю этой матрицы.

ё)Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.

ж) Определитель произведения квадратных матриц равен произведению определителей этих матриц.

з)если строку\столбец матрицы умножить на число, то ее определитель увеличится на это число.

и)если сложить поэлементно 2 строки\столбца, одну из них домножив на число, то определитель не изменится.

к)определитель матрицы треугольного вида = произведению её главной диагонали

1.Понятие обратной матрицы

Рассмотрим квадратную матрицу А порядка n с элементами и определителем отличным от нуля. Такие матрицы в дальнейшем будем называть невырожденными.

Квадратные невырожденные матрицы А и В порядка n называются взаимно обратными, если их произведение коммутативно и равно единичной матрице, т.е. АВ=ВА=Е. Обратная матрица к матрице А обозначается символом и удовлетворяет условию А=А=Е.

Существование обратной матрицы

Теорема . Для того чтобы матрица А имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля, т.е. матрица А невырожденная.

НА КЛЕЧ.ЛИСТКЕ.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Векторы и операции над ними

1.Скаляры и векторы.

Величины, встречающиеся в естествознании, бывают двух типов. С одной стороны, это те величины, которые характеризуются только числовым значением: масса, площадь, длина, температура и т.д. С другой стороны, величины, которые определяются своим числовым значением и направлением: сила, скорость, ускорение и другие.

Величины первого типа называются скалярными или скалярами, а величины второго типа называются векторными.

Всякую векторную величину в физическом пространстве геометрически можно изобразить отрезком определенной длины и определенного направления - направленным отрезком.

Вектором будем называть направленный отрезок, имеющий начало в точке А и конец в точке В. Вектор часто обозначают одной буквой, например, .

Модулем или длиной вектора = называют длину отрезка АВ и обозначают символом а.

Вектор, начало и конец которого совпадают, т.е. , будем называть нуль-вектором и обозначать символом . Направление нуль-вектора можно выбирать произвольно.

Два вектора и называются равными, если:

Длины векторов равны, т.е. = ;
Векторы и параллельны, т.е. расположены на параллельных или совпавших прямых;
Векторы и одинаково направлены (рис. 7).

Рис.7

В дальнейшем условимся не различать равные векторы, т.е. множество равных векторов будем понимать как один вектор, имеющий начало в произвольной точке, так называемый свободный вектор.

2.Сложение векторов.

Суммой векторов , , будем называть вектор , начало которого совпадает с началом первого вектора, а конец совпадает с концом последнего вектора, при условии что начало последующего вектора совпадает с концом предыдущего (рис. 8)

Замечание. Для сложения двух векторов можно воспользоваться «правилом параллелограмма»: суммой двух векторов и называется третий вектор , имеющий общее начало с векторами и и совпадающий с диагональю параллелограмма, построенного на этих векторах (рис. 9).

Операция сложения векторов обладает свойствами:

+=+;
+(+)=(+)+
+=;
Вектор - называется противоположным вектору ; вектор - имеет длину равную длине вектора , но противоположное направление, т.е. +(-)=.

3.Вычитание векторов.

Разностью двух векторов и будем называть сумму векторов и -, т.е. +(-) (рис. 10).

4.Умножение вектора на число.

Произведением вектора на число называется вектор длины

= а, направление которого совпадает с направлением , если , противоположно , если < . При =0 =0.

Операция умножения вектора на число обладает свойствами:

( + ) =+, R;
(+)=+;
()=();
1=, (-1) =-, 0=.

Замечание. Вектор называется единичным вектором или ортом направления, определяемого вектором . Очевидно имеет место равенство =а.

5.Коллинеарные векторы.

Два вектора и называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.

Заметим, что нулевой вектор коллинеарен любому вектору.

Теорема 1. Для того чтобы два вектора и были коллинеарны необходимо и достаточно, чтобы они были пропорциональны, т.е. имело место равенство =, R.

6.Компланарные векторы.

Три или более векторов называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Теорема 2. Для того чтобы три вектора , , были компланарными необходимо и достаточно, чтобы один из них был линейной комбинацией двух других, т.е. = +, ,R.

Доказательство.

Необходимость. Пусть векторы , , компланарны, расположены в одной плоскости и имеют общее начало О (этого можно достичь параллельным переносом).

Предположим сначала, что среди этих векторов существуют два неколлинеарных вектора, например и . Тогда представляя вектор в виде суммы векторов и , соответственно коллинеарных и , будем иметь

=+ (рис. 11)

Так как векторы и , и попарно коллинеарны, то = = и = +. Если все три вектора коллинеарны, то вектор можно представить в виде = +0

Достаточность. Пусть векторы , , удовлетворяют условию =+. В этом случае вектор лежит в той же плоскости, что и векторы и , в силу определенных операций: сложения векторов и умножения вектора на число.

Теорема доказана.

Проекция вектора на ось.

Проекцией вектора на ось Z наз. число =, где - угол между вектором и направлением оси Z.

Если =, то проекция его на любую ось равна нулю.

Проекция вектора на ось Z обозначается символом = (рис. 12).

Вектор называется составляющей вектора по оси Z, причем =, где - орт оси Z.

Замечание. Проекция вектора на ось Z положительна, если (рис. 12а), равна нулю, если , и отрицательна, если (, (рис. 12б). Проекции равных векторов на одну и ту же ось равны между собой.

Теорема 3. Проекция суммы векторов на данную ось равна сумме проекций этих векторов на ту же ось, т.е. (++)=++.

Доказательство.

Пусть заданы векторы , , , суммой которых является вектор (рис.13). Тогда имеем .

Однако , откуда и получаем .

Теорема 4. При умножении вектора на число его проекция на данную ось умножается на то же число, т.е. ()=.

Доказательство.

Из определения проекции вектора на ось Z имеем: =₁, ()=₂, где ₁, ₂ - значения углов, которые составляют векторы и с осью Z. В случае >0, cos ₁=cos ₂, получаем =₁=.

Если же <0, - cos ₁=cos ₂, то =₂=- (-cos ₁)= . При =0 имеем ==0.

Теорема доказана.

Свойства проекции

Скалярное произведение векторов

Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов и косинуса угла между ними.

Скалярное произведение векторов и обозначается символом или (,) , т.е. (,)=ab cos (рис. 3).

Вспоминая понятие проекции вектора на ось, можно заключить следующее: скалярное произведение двух векторов и равно длине одного из них умноженной на проекцию другого на направление первого, т.е. (,)=

Свойства скалярного произведения векторов:

(,)=(,) - следствие определения,
- так как =
- так как ,
- так как ,
- следствие свойств 2 и 4.

Заметим, что косинус угла между не нулевыми векторами и находится по формуле Cos = (2)

Из равенства (3.2) следует, что ненулевые векторы и перпендикулярны лишь в том случае , если их скалярное произведение равно нулю, т.е. (,)=0; Cos =0; .

Замечание. Нулевой вектор считается перпендикулярным любому другому вектору.

Некоторые следствия.

1.Проекция вектора на направление вектора равна скалярному произведению вектора на орт вектора .

Действительно, если векторы и образуют между собой угол , то где орт вектора .

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.

На самом деле, если векторы и заданы в координатной форме, т.е.

Тогда имея в виду свойства скалярного произведения, и т.к.

, , получим

3. Косинус угла между двумя векторами и , заданных координатами, определяется по формуле . Данная формула является следствием (2)

4. Два вектора коллинеарны в том и только в том случае, если их соответствующие координаты пропорциональны. Действительно, условие коллинеарности векторов и = в координатной форме имеет вид

. Из этого равенства следует наше утверждение, так как

Верно и обратное.

Векторное произведение двух векторов

Предварительно введем понятие правой тройки векторов. Три вектора , , образуют правую тройку, если движение вектора к вектору по меньшему углу совершается против часовой стрелки, при наблюдении с конца вектора .

Например, орты ,, правой системы координат образуют правую тройку векторов. Векторным произведением двух векторов и называется третий вектор , обозначаемый символом и удовлетворяющий условиям:

1.Модуль вектора равен площади параллелограмма, построенного на векторах и т.е., , где -угол между этими векторами.

Вектор ортогонален векторам и .

Тройка векторов , , правая.

Свойства векторного произведения.

=- . Действительно, модуль векторного произведения не меняется, т.к. численно равен площади параллелограмма, построенного на векторах и ; направление противоположно направлению , т.к. движение от вектора к вектору по меньшему углу с конца вектора -( ) видно по направлению против часовой стрелки, (рис. 4).

Указанное равенство следует из определения.

Замечание: Для того чтобы векторы были коллинеарны необходимо и достаточно, чтобы их векторное произведение было равно нуль вектору, т.е. =.

Докажем равенство = при .

Пусть ()= и =abSin. Тогда вектор имеем то же направление, что и вектор . Но , значит или =. Очевидно, что =.

4.Для любых векторов , , имеет место равенство (+)= . Рассмотрим частный случай: пары векторов , и , -правые. В этом случае векторы ( также образуют правую пару. Тогда векторы , , коллинеарны и одинаково направлены. И нам остается доказать, что модуль вектора равен сумме модулей векторов и , т.е. + .

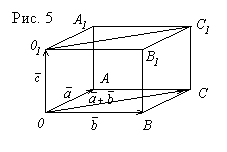
Рассматривая соответствующие параллелограммы, (рис. 5), имеем ,.

Так как , то имеет место равенство площадей

. Откуда + , а значит

=+. Таким образом векторное произведение сумм векторов осуществляется

по правилу умножения многочленов.

5.Векторное произведение в координатах.

Пусть даны два вектора и в координатах, т.е.

, .

Тогда, используя свойства векторного произведения и условия

, ,

получим =.

Или =,

откуда =.

Замечание. Так как ² можно представить в виде

²=,

то площадь S треугольника, построенного на векторах и можно вычислить по формуле S=1/2 или

Первый замечательный предел. =1

Рассмотрим тригонометрический круг. Имеем

|AC|=sin x

|BmC|=x

BD=tg x

Очевидно, что sin x< x <tg x ( при 0< x </₂).

Разделим неравенство на sin x0, тогда

1< или 1>>cos x

0>-1>cos x-1; 0< 1-<2sin²<2=

Так как 0 и есть бесконечно малые функции при х0, то и 1- при õ0 бесконечно малая функции. Значит =1.

Замечание. Доказательство проведено для х>0. Однако, если х<0, то под знаком предела можно сделать замену х=-t, t+0: ===1.

Следовательно =1

Признаки существования предела

1. Если и , то

2. Монотонная и ограниченная последовательность имеет предел.

3. Числовая последовательность (xn) имеет конечный предел тогда и только тогда, когда

Предел функции в точке.

Прежде чем рассматривать предел функции, введем некоторые понятия.

А. Предельная точка множества.

Определение. Точка х₀ называется предельной точкой множества Х или точкой сгущения, если в любой окрестности точки х₀ содержится хотя бы одна точка множества Х отличная от х₀.

Например. 1. Любая точка замкнутого промежутка является точкой сгущения этого промежутка.

Любой частичный предел последовательности является точкой сгущения для последовательности.

Любая точка интервала (a, b) и точки a, b являются предельными для множества (a, b).

Как видим из приведенных примеров, что предельные точки множества могут как принадлежать, так и не принадлежать множеству, для которого они являются предельными.

Например. 1. х_n=(-1)ⁿ - последовательность имеет две предельные точки: 1 и -1

x_n=1/n - последовательность имеет одну предельную точку 0;

[0; 1] - все точки множества являются предельными ;
(a, b) - все точки множества [a, b] являются предельными для этого множества;
Предел последовательности всегда является предельной точкой последовательности.

Б. Окрестность.

Определение. Любой открытый промежуток (х₀-; х₀+) называется

- окрестностью точки х₀ и обозначается (х₀).

Определение. Левой полуокрестностью точки х₀ является

множество (х₀-, х₀), а правой полуокрестностью точки х₀ является множество (х₀, х₀+).

Определение. Окрестностью бесконечности будем называть множества:

(-; -)( ; +), где некоторое положительное число.

Замечание. Окрестностью + является множество ( ; +), а окрестностью - является множество (-; -) , где некоторое положительное число.

Очевидно, что любая окрестность предельной точки множества содержит бесконечно много точек этого множества.

В. Замкнутость множества. Граница множества.

Определение. Множество Х называется замкнутым, если оно содержит все свои предельные точки.

Определение. Множество Х называется открытым, если всякая его точка принадлежит этому множеству вместе с некоторой окрестностью.

Определение. Граничной точкой множества Х называется точка х₀, в любой окрестности которой лежат как точки множества Х, так и точки, которые ему не принадлежат.

Определение. Множество всех граничных точек образует границу данного множества.

Замечание. Граничная точка множества Х может не принадлежать этому множеству.

Примеры.

Множество [0; 2] является замкнутым; так как все его предельные точки (а это сам отрезок [0;2]) принадлежат данному множеству.

Множество (0; 2) является открытым, так как все его точки принадлежат множеству (0; 2) вместе с некоторой окрестностью. (При этом предельные точки 0 и 2 не принадлежат данному множеству).

3. Множества (0; 2] и [0; 2) не являются ни замкнутым ни открытым, т.к.:

1). не все предельные точки их принадлежат данному множеству

(точка 0 предельная для (0, 2], но ему не принадлежит; точка 2 предельная для [0, 2), но ему не принадлежит;

2). не все точки принадлежат множеству вместе с некоторой

окрестностью (точка 2 для (0; 2] не принадлежит ему вместе с окрестностью; точка 0 для [0, 2) не принадлежит ему вместе с окрестностью)

То есть существуют множества, которые не являются ни открытыми ни замкнутыми.

4.Для множеств [0, 2], (0, 2), [0, 2), (0, 2] точки 0 и 2 являются граничными, причем:

1). граничные точки 0 и 2 принадлежат [0, 2];

2). граничные точки 0 и 2 не принадлежат (0, 2);

3). граничная точка 0 принадлежит [0, 2), а граничная точка 2 не принадлежит [0, 2);

4). граничная точка 0 не принадлежит (0, 2], а граничная точка 2 принадлежит (0, 2].

Далее рассмотрим два примера: y=1/x, y=x+1.

Указанные функции обладают такими свойствами:

- значение первой функции у=1/х становится близким к 0, если значение аргумента х становится достаточно большим, например положительным.

- значение второй функции становится близким к 2, если значение аргумента х становится близким к 1.

В математике эти факты можно записать символами:

у=1/х0, при х; у=х+12, при х1.

Это свойство можно строго сформулировать математически и оно имеет большое значение в математике.

Определение предела (по Коши). Функция f(x) хХ имеет своим пределом число А при стремлении x к предельной точке х₀ множества Х, если для каждого числа >0 существует число ()>0 такое, что при всех х из окрестности |x-x₀|<, xx₀ имеет место неравенство |f(x)-A|<.

Символически этот факт записывают в виде .

Геометрическая интерпретация.

Если функция у=f(x) хХ имеет своим пределом число А при хх₀, то разность значений функции и ее предела А достаточно мала, если значение аргумента х близко к х₀.

Геометрически это означает, что график функции y=f(x) виден в «окошке» плоскости OXY c координатами: х(х₀-; х₀+), хх₀, =min(₁, ₂); y(A-; A+), А - предел функции, - любое положительное число.

Особо отметим, что график функции может «выйти» из указанного «окошка» только через боковые стороны. Только через них!

Отметим еще одну особенность: при рассмотрении предела функции в точке х₀ само значение функции в точке х₀ исследователя не интересует. Это значение f(x₀) может быть, в общем случае, равным А или не равным А, или, наконец, функция f(x) в точке х₀ может быть не определена.

Определение предела (по Гейне). Функция f(x) хХ имеет своим пределом число А при стремлении х к предельной точке х₀, если для любой последовательности x_n сходящейся к х₀, причем x_nх₀ ( x_n X ) последовательность f(x_n) сходится к А.

Символическая запись.:

По Коши: для >0, (, x₀)>0, что при |x-x₀|<(), xx₀ => |f(x)-A|<.
По Гейне: для x_nx₀, x_nx₀ => f(x_n)A.

Отметим, что определения предела функции в точке по Коши и по Гейне -

эквивалентны.

Сформулируем далее следующие утверждение: число А не является пределом функции f(x) в точке х=х₀.

Данное утверждение обычно называют отрицанием предела.

Отрицание предела. А.

По Коши : ₀>0 такое, что для >0 существует точка х*Х такая, что |x*-x₀|<, x*x₀, но |f(x*)-A|₀.

По Гейне : x_n*x₀, x_n*x₀, что f(x_n*) / A.

Свойства пределов

Пусть даны функции и .

1.Одна и та же функция в одной и той же точке может иметь только один предел.

2.Сходящаяся функция локально сохраняет знак. Более обще,

где — проколотая окрестность точки a.

3.В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:

4.Сходящаяся функция локально ограничена в окрестности предельной точки:

5.Отделимость от нуля функций, имеющих предел, отличный от нуля.

6.Операция взятия предела сохраняет нестрогие неравенства.

7. Предел суммы равен сумме пределов:

8. Предел разности равен разности пределов:

9. Предел произведения равен произведению пределов:

10. Предел частного равен частному пределов.

Второй замечательный предел.

Мы уже встречались ранее с пределом (1+1/n)ⁿ=e при nN . Очевидно (1+1/n_k)^nk=e, при n_kN, т.к. последовательность (1+1/n_k)^nk является подпоследовательностью сходящейся к е, последовательности (1+1/n)ⁿ.

Возьмем далее произвольную последовательность х_ксходящуюся к +, т.е. х_к+, при к.

Тогда имеем n_kx_k<n_k+1, где n_k=[x_k], а также ; ; .

То есть. Пределы левой и правой частей при к равны е, т.к. n_k+ (очевидно и х_к+) и (1+1/n_k)^nk=e. Откуда по теореме о зажатой последовательности имеем

(1+1/х_k)^х^k=e при х_к+.

Тогда по определению предела по Гейне получаем, что

(1+1/х)^х=e - 2^ой замечательный предел.

Имеет место также равенство (1+1/х)^х=e т.к. сделав замену -х=t , получим: (1-1/t)^-^t== == e

=e.

Итак

Замечание.

Следует отметить, что (1+(х))^1/(х)=е ;

(1+¹/_(х))^(х)=е

Не забудьте!!! В формуле 2 ^ого замечательного предела всегда «добавка» к единице является бесконечно малой, а показатель степени является обратной величиной этой бесконечно малой.

Определение непрерывности функции в точке.

Предположим, что нам задана функция f(x), определенная в некоторой области X={x}, причем полагаем, что предельная точка х=х₀ является внутренней точкой множества Х.

Замечание. При определении предела функции было не обязательно, чтобы предельная точка х=х₀ принадлежала множеству области определения f(x).

Определение. Функция f(x) называется непрерывной в точке х=х₀, если она имеет этой в точке предел равный значению f(x₀), т.е. f(x)=f(x₀).

Определение по Коши. Функция f(x) непрерывна в точке х=х₀,

если по >0, ()>0 такое, что при всех х из |x-x₀|< => |f(x)-f(x₀)|< .

Определение по Гейне. Функция f(x) непрерывна в точке х=х₀, если для любой сходящейся к х₀ последовательности x_nx₀, имеем f(x_n)f(x₀).

Важно отметить, что равенство f(x)=f(x₀) можно записать в виде f(x)=f(x).

То есть для непрерывных функций возможно переставить местами символы «функция» и «предел», что очень важно при вычислении пределов.

Определению непрерывности функции f(x) в точке х=х₀ можно придать другую форму : дадим аргументу х в точке х=х₀, приращение х=х-х₀, тогда разность f(x)-f(x₀)=y представляет собой приращение функции в точке х=х₀, соответствующее приращению аргумента х, т.е. уf(x₀)=f(x₀+x)-f(x₀).

Из определения непрерывности f(x) следует, что при х0 (хх₀) имеет место у0 (f(x)f(x₀)), т.е. у=0.

((f(x₀+х)-f(x₀))=0).

Итак, непрерывная в точке функция характеризуется тем, что бесконечно малому приращению аргумента х соответствует бесконечно малое приращение функции у.

Задачи, приводящие к вычислению производной.

а. Скорость точки в данный момент.

Пусть S(t) функция времени, выражающая расстояние пройденное точкой за время t. Рассмотрим изменение этой функции от момента времени t за промежуток равный t : S(t)=S(t+t)-S(t). После чего вычислим среднюю скорость точки на промежутке времени [t, t+t] V_ср=.

Если мы хотим найти скорость точки в данный момент (мгновенную скорость), а именно в момент времени t, нужно вычислить предел V_ср=.

Таким образом находим скорость изменения функции S(t) в момент времени t.

б. Линейная плотность стержня.

Если стержень является неоднородным, то очевидной характеристикой стержня является плотность его в данной точке, которая определяется как отношение массы стержня к его длине. Находим среднюю плотность стержня на промежутке [x, x+x]

_c_р==

Тогда плотность стержня в точке х выразится пределом

(х)= _c_р=.

в. Задача о касательной к кривой.

Пусть уравнение y=f(x) задает в плоскости Оху, некоторую кривую l . Для данной кривой ставится задача : определить наклон касательной к этой кривой, проведенной в точке (x, f(x)), т.е. определить тангенс угла между касательной и положительным направлением оси Ох. При этом касательной к кривой l в точке (x, f(x)) называется предельное положение секущей, проходящей через точки (x, f(x)) и (x+x, f(x+x))

при х0.

Находим тангенс угла наклона секущей L:

tg ==

tg =, где - угол наклона касательной к кривой в точке (x, f(x)), который она составляет с положительным направлением оси Ох. Из приведенных примеров следует, что многие практические задачи физики, геометрии и техники сводятся к вычислению предела частного, в числителе которого стоит приращение функции, а в знаменателе приращение аргумента, вызвавшее это приращение.

Производная функции в точке.

Определение. Производной функции y=f(x) в точке называется предел отношения приращения функции (у) в этой точке к соответствующему приращению аргумента (х) при стремлении последнего к нулю, то есть

y'(x)= при условии, что этот предел существует. Принято обозначать производную функции у=f(x) в точке х как y'(x) или .

Дифференциа́л — линейная часть приращения функции.

Дифференцируемость функции.

Определение. Функция y=f(x) называется дифференцируемой в точке х, если приращение у функции f(x) в точке х, отвечающее приращению аргумента х, может быть представлено в виде у=Ах+(х)х, где А - постоянное число (для точки х), не зависящее от х; (х) - бесконечно малая функция х, т.е. (х)=0.

Иначе говоря, приращение у имеет вид у=Ах+о(х).

Далее покажем дифференцируемость некоторых функций.

у=х²+2. у=(х+х)²+2-х²-2=2хх+х². А=2х; (х)=х.
у=ln x. y=ln(x+x)-ln x=ln(1+x/x)=x/x+о(x)
у=sin x. y=sin(x+x)-sin x=2sin(x/2)cos(x/2+x)=

=2(^x/₂+о(x))[cos x+(cos(x+^x/₂)-cos x)]=

=[x+2о(x)]cos x-[x+2o(x)]sin(x+^x/₄)sin^x/₂=

=[x+2о(x)]cos x-[x+2о(x)][^x/₂+о(x)]sin(x+^x/₄)=

=cos x x+2cos xо(x)-(x)²(f(x, x))=cos x x+о(x).

Теорема. Для того чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно чтобы f(x) имела в этой точке производную.

Доказательство.

Необходимость. Пусть y=f(x) в т. х дифференцируема, тогда у=Ах+о(х). Разделим у на х и вычислим предел частного при х0 :

=(А+)=А.

С другой стороны =f '(x). Значит f '(x) существует и равна А.

Достаточность. Пусть функция y=f(x) имеет производную, т.е. =у'(x), тогда разность функции и предела y'(x) есть величина бесконечно малая при х0, т.е. -y'(x)=(х); (х)0 прих0, у=y'(x)x+(x)x. Пусть y'(x)=A для точки х, тогда у=Ах+(х)х.

Теорема доказана.

Теорема. Дифференцируемая в точке х функция y=f(x) непрерывна в этой точке.

Доказательство. Так как у=Ах+о(х) - условие дифференцируемости, то при х0 получаем у0. Последнее означает непрерывность функции f(x) в точке х.

Замечание. Дифференцируемая в точке х=х₀ функция у=f(x) имеет в точке (х₀; f(x₀)) касательную прямую.

Геометрический смысл производной.

Тангенс угла наклона касательной, проведенной в точке (x, f(x)) к кривой l: y=f(x), который она составляет с положительным направлением оси Ох, численно равен производной функции y=f(x) в точке х, то есть tg=y'(x).

Уравнение касательной к кривой.

Теорема. Уравнение касательной к кривой y=f(x) в точке (х₀, f(x₀)) имеет вид y-y₀=f '(x₀)(x-x₀).

Доказательство. Известно, что уравнение прямой имеет вид y=kx+b. Но так как эта прямая является касательной к кривой l: y=f(x) в точке (x₀, f(x₀)) , то ее угловой коэффициент k должен быть равен f '(x₀) . Чтобы найти b, воспользуемся тем, что касательная проходит через точку (x₀, f(x₀)). Значит b=f(x₀)-kx₀. Откуда получаем b=y₀-f '(x₀)x₀, здесь y₀=f(x₀). Подставляя в уравнение прямой у=kx+b найденные значения k и b, получим уравнение касательной к кривой l, проходящей через точку (x₀, f(x₀)): y-y₀=f '(x₀)(x-x₀).

Пример. Найти угловые коэффициенты касательных к параболе у=2х²-2 в точках, абсциссы которых соответственно равны х₁=1, х₂=-2.

Решение. Вычислим производные функции f(x) в точках х₁=1, х₂=-2: так как у'=4x, то y'(1)=4, y'(-2)=-8. Значит искомые угловые коэффициенты соответствующих касательных будут равны k(1)=4 и k(-2)=-8.

Пример. Написать уравнение касательных к параболе у=х²+1 в точках (1; 2) и (0; 1).

Решение. Находим угловые коэффициенты касательных в соответствующих точках k₁=y'(1)=2 и k₂=y'(0)=0. Тогда имеем уравнения касательных у-2=2(х-1) и у-1=0.

Производная сложной функции.

Теорема. Пусть нам задана сложная функция y=f((x)), причем

Функция u=(x) имеет в точке х* производную u'='(x*);
функция y=f(u) имеет в точке u*=(x*) производную y'=f'(u*), тогда сложная функция y=f((x)) в точке х* также имеет производную, которая выражается формулой

[f((x))]'=f'((x*))_x'(x*), или [f((x))]_x'=f'_x'.

Доказательство. Найдем приращение f в точке х*, которое соответствует приращению аргумента х:

Т.к. =_х'x+(x)x, и f=f'+(), то f=f'(_x'x+x(x))+() .

И =(f'_x'+f' (x)+())=f'_x'.

Окончательно имеем f_x'((x))=f'_x'.

Производная неявной функции.

Пусть значения двух переменных х и у связаны между собой уравнением вида F(x, y)=0.

Пример: у+=0 , x²+ln y=0.

Определение. Если функция y=f(x), определенная на некотором интервале (a, b) такова, что уравнение F(x, y)=0 при подстановке в него y=f(x) обращается в тождество относительно х, то функция у=f(x) называется неявно заданной уравнением F(x, y)=0.

Частные производные функции z=F(x, y).

Определение. Если существует предел , то он называется частной производной по переменному х функции z=F(x, y) в точке (х, у) и обозначается символами z_x' или F_x'(x, y).

Определение. Если существует предел , то он называется частной производной по переменному у функции z=F(x, y) в точке (х, у) и обозначается символами z_y' или F_y'(x, y).

Полное приращение F(x, y)

Пусть имеем функцию двух переменных z=F(x, y), где у=f(x) дифференцируемая функция; т.е. F(x, y) является функцией переменного х как сложная функция z=F(x, f(x)). Если переменная х получает приращение х, то переменная у=f(x) также принимает приращение у в силу непрерывности f(x). Откуда получим:

F(x)=F(x+x, y+y)-F(x, y)=F(x+x, y+y)-F(x, y+y)+F(x, y+y)-F(x, y)= =_xF(x, y+y)+_yF(x, y). тогда после деления равенства на х и перехода к пределу при х0 получим:

=+=+ =F_x'(x, y)+F_y'(x, y)y'(x)

Итак: для того чтобы вычислить производную функции у=f(x), заданной неявно уравнением F(x, y)=0, нужно приравнять нулю производную левой части как производную сложной функции, считая у функцией х, т.е. у=f(x). При этом получим равенство F_x'+F_y'y_x'=0 или y_x'=. F_y'0.

Здесь F_x' и F_y' - частные производные F(x, y) по переменным х и у соответственно.

Например.

х²+у²-а²=0. 2х+2yy'=0, y_x'=-x/y; y0.
sin x+yx=0. cos x+y+y'x=0, y_x'= (-y-cos x)= (-cos x+). x0.

Производная обратной функции.

Напомним условия существования обратной функции.

Теорема. Если функция f(x) определена, строго монотонна и непрерывна на отрезке [a, b] , то существует однозначная, строго монотонная и непрерывная функция x=(y) обратная функции у=f(x) на промежутке [f(a), f(b)].

Замечание. Чтобы по данной функции у=f(x) построить обратную функцию, надо разрешить уравнение y=f(х) относительно х (если это удается), т.е. выразить х через у : х=(у).

Например. y=cos x и x=arccos y; y=a^x и x=log_aу.

Теорема. Пусть на отрезке [a, b] задана строго монотонная, непрерывная функция y=f(x), тогда, если в точке х* функция y=f(x) имеет конечную производную f'(x*)0, то производная обратной функции х=(у) в точке у* (у*=f(x*)) существует и находится из равенства

(y*)=.

Доказательство. Дадим приращение у переменной у в точке у*, тогда обратная функция х=(у) получит соответствующее приращение х=(у*). Заметим, что приращения х и у отличны от нуля, так как функции (у) и f(x) строго монотонны. Далее составим частное . При переходе к пределу при у0 (очевидно х0), получим x_y(y*)===. Следовательно (y)|_y₌_y_* =.