§ 7.3. Связь между матрицами линейного оператора в разных базисах. Действия с линейными операторами

Пусть из - мерного пространства в - мерное пространство действует линейный оператор и пусть он имеет матрицу в паре базисов и линейных пространств и и матрицу - в паре базисов и пространств и . Тогда матрицы и оператора связаны соотношением

, (7.3.1)

где - матрица перехода от базиса к базису пространства , - матрица перехода от базиса к базису пространства .

В частности, если пространства и совпадают, то базисы и также совпадают, и формула (7.3.1) принимает вид

. (7.3.2)

Матрицы и , связанные соотношением (7.3.1), называют эквивалентными, а матрицы и , связанные соотношением (7.3.2), подобными, причем говорят, что матрица получается из матрицы трансформированием матрицей .

В § 7.1 мы уже ввели операции сложения операторов и умножения их на числа. Напомним, что сумма линейных операторов и произведение линейного оператора на число являются линейными операторами.

Пусть теперь , . Произведением оператора на оператор называется оператор , действующий из в и определяемый соотношением

. (7.3.3)

Для того чтобы произведение операторов имело смысл, необходимо и достаточно, чтобы образ оператора содержался в области определения оператора . Это условие заведомо выполнено, если рассматриваются операторы из . Произведение линейных операторов является линейным оператором.

Выберем в линейных пространствах базисы , и соответственно и обозначим матрицу оператора в паре базисов и через , матрицу оператора в паре базисов и - через . Тогда оператор в паре базисов и имеет матрицу (матрица оператора, действующего первым, пишется в произведении справа).

Линейный оператор , действующий в - мерном пространстве называют невырожденным, если дефект этого оператора равен нулю или, что то же самое, если ранг равен . Для вырожденного оператора существует, причем единственный, линейный оператор такой, что

, (7.3.4)

где - единичный оператор. Оператор называют оператором, обратным к оператору и обозначают . Если в некотором базисе невырожденному оператору отвечает невырожденная матрица , то в этом же базисе обратному к данному оператору соответствует матрица .

Пример 1. Линейный оператор в базисе , имеет матрицу . Найдите его матрицу в базисе , .

Решение. Матрица оператора в базисе связана с матрицей этого же оператора в базисе соотношением

.

Найдем матрицу перехода от базиса к базису . Для этого разложим векторы базиса по векторам базиса :

и решим записанные системы линейных алгебраический уравнений относительно :

.

Следовательно, и матрица . В силу того, что и , окончательно получаем:

.

Пример 2. Линейный оператор, действующий из пространства в пространство задан в стандартных базисах матрицей . Вычислите матрицу этого оператора в базисах и .

Решение. Запишем стандартные базисы и линейных пространств и соответственно: , ; . Матрица оператора в паре базисов и связана с матрицей оператора в паре базисов и соотношением

.

Матрицы перехода и , соответственно, от базиса к базису и от базиса к базису в данном случае находятся элементарно. Поскольку

и ,

.

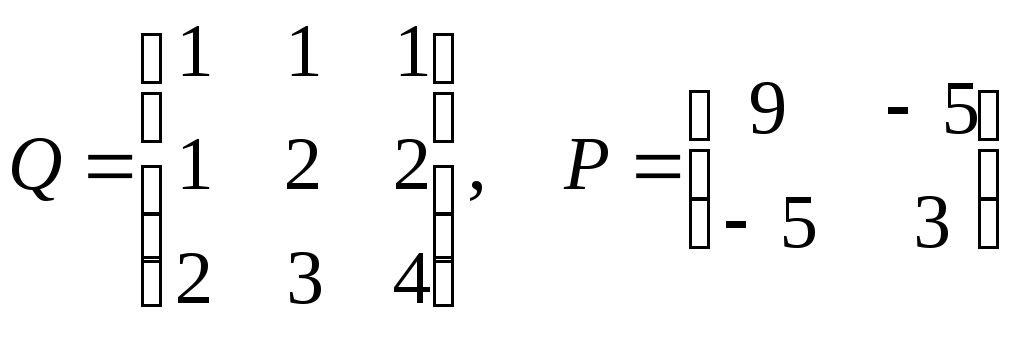Учитывая, что 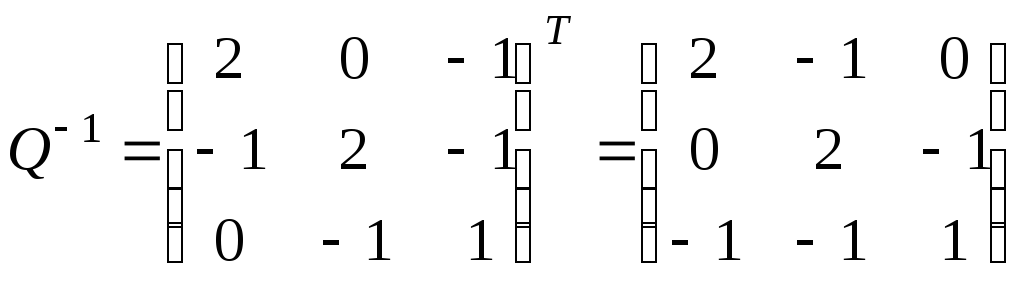, имеем:

.

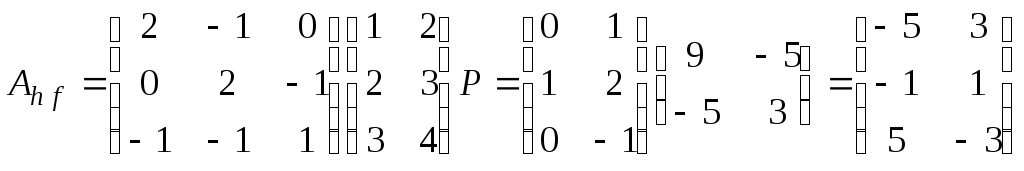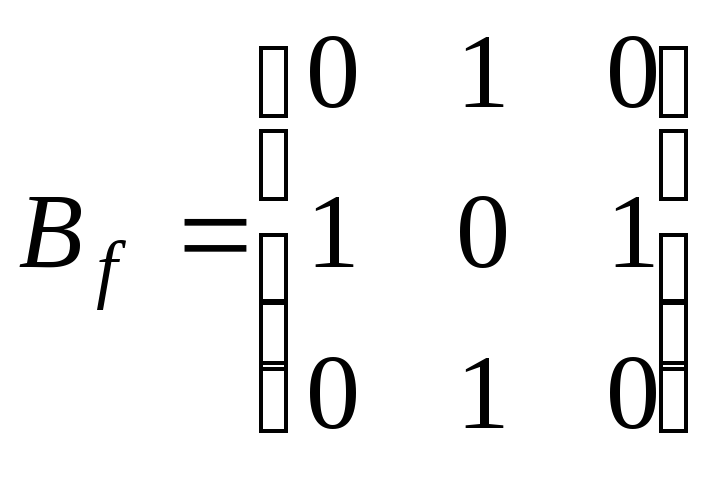Пример 3. Пусть линейный оператор пространства имеет в базисе матрицу , а оператор в базисе - матрицу . Найдите матрицы линейных операторов в базисе .

Решение. В силу того, что

,

начнем с нахождения матрицы оператора в базисе . Матрица связана с матрицей соотношением

.

Учитывая, что

матрица перехода от базиса к базису . Поскольку

,

.

Следовательно,

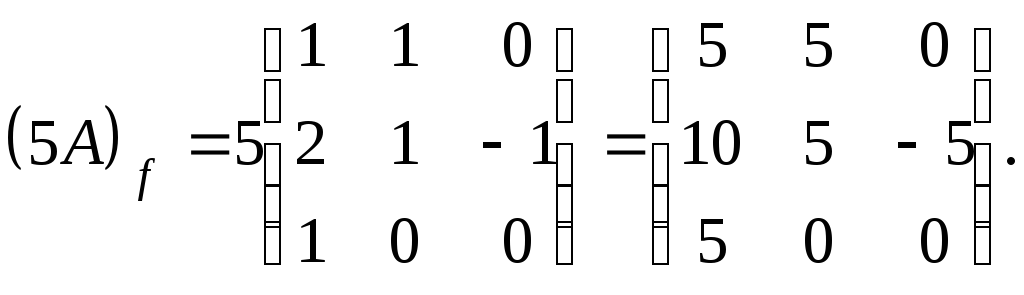
7.3.1. Линейный оператор в базисе имеет матрицу . Найдите его матрицу в базисе .

7.3.2. Линейный оператор в базисе имеет матрицу . Найдите его матрицу в базисе , , .

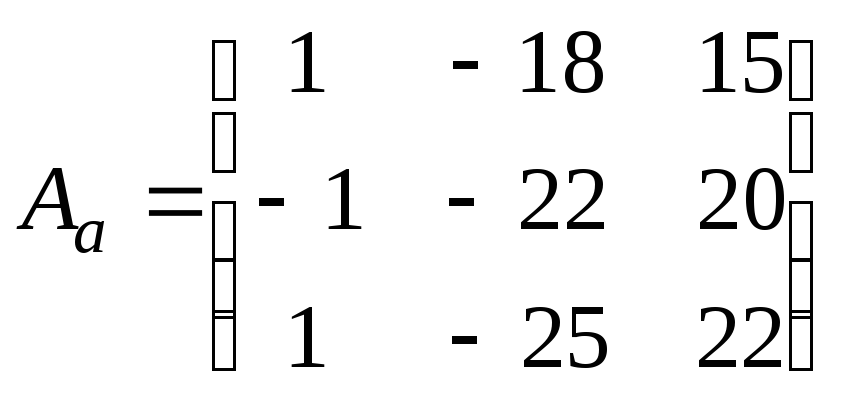7.3.3. Линейный оператор в базисе , , имеет матрицу . Найдите его матрицу в базисе , , .

7.3.4. Докажите, что преобразование трёхмерного пространства , где является линейным преобразованием, и найдите его матрицы в ортонормированном базисе , в котором даны координаты всех векторов, и в базисе , , .

7.3.5. Как изменится матрица линейного преобразования, если в базисе поменять местами два вектора ?

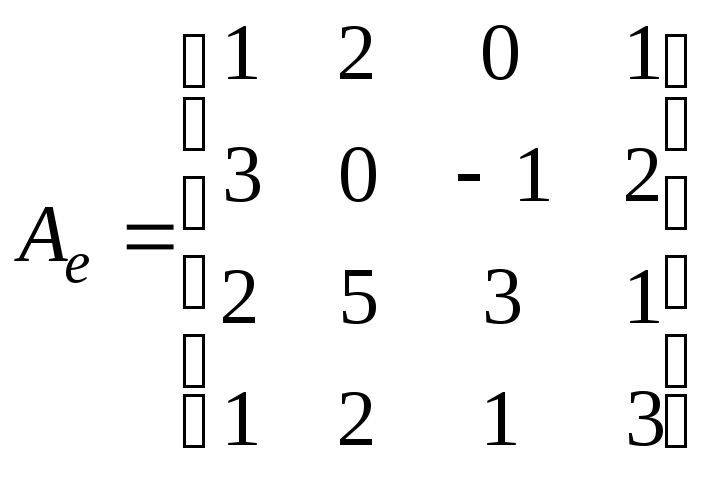7.3.6. Линейный оператор в базисе имеет матрицу . Найдите матрицу этого же оператора в базисе:

;

.

7.3.7. Линейный оператор, действующий из пространства в пространство задан в стандартных базисах матрицей . Вычислите матрицу этого оператора в базисах и .

, , , , , ;

, , , , , , ;

, , , , , , , .

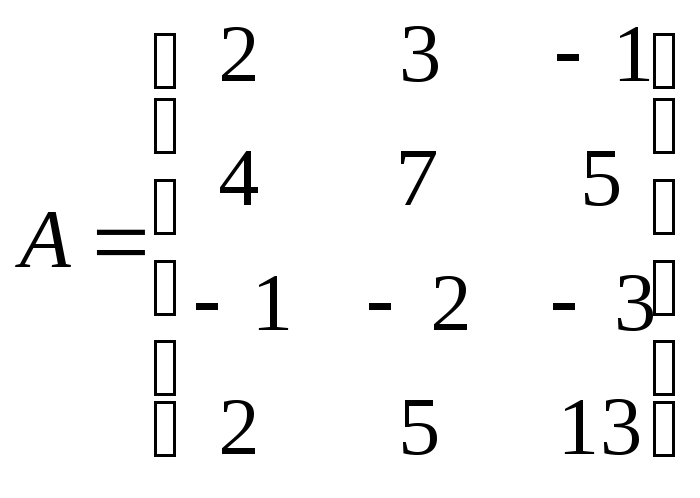7.3.8. В базисе , , , пространства линейный оператор задан матрицей . Найдите матрицу этого оператора в базисе , , , .

7.3.9. Линейный оператор в базисе , имеет матрицу , а линейный оператор в базисе , - матрицу . Найдите матрицу линейного оператора в том базисе, в котором даны координаты всех векторов.

7.3.10. Линейный оператор переводит векторы , , в , , , а линейный оператор переводит , , в , , соответственно. Найдите матрицу оператора

в исходном базисе;

в базисе ;

в базисе .

7.3.11. Пусть - линейные преобразования пространства , имеет матрицу в стандартном базисе, а - матрицу в базисе , . Вычислите матрицу оператора:

в стандартном базисе;

в базисе ;

в базисе , .