
- •Глава 7 линейные операторы в линейных пространствах
- •§ 7.1. Определение линейного оператора.
- •Матрица линейного оператора
- •§ 7.2. Связь между координатами вектора - образа и вектора - прообраза. Ядро и образ линейного оператора
- •§ 7.3. Связь между матрицами линейного оператора в разных базисах. Действия с линейными операторами
Светлой памяти
Чубича Михаила Петровича
посвящается
Глава 7 линейные операторы в линейных пространствах
§ 7.1. Определение линейного оператора.
Матрица линейного оператора
Пусть
![]() и
и ![]() - линейные пространства над одним и тем
же полем
- линейные пространства над одним и тем
же полем ![]() .
Будем говорить, что из
пространства
.
Будем говорить, что из
пространства
![]() в пространство
в пространство
![]() действует оператор
действует оператор
![]() или, что то же самое, отображение
или, что то же самое, отображение
![]() ,
преобразование
,
преобразование
![]() ,
если каждому вектору
,
если каждому вектору ![]() по какому - либо правилу поставлен в
соответствии определенный вектор
по какому - либо правилу поставлен в
соответствии определенный вектор ![]() из
из ![]() .
.
Наиболее
простыми являются линейные операторы.
Отображение ![]() называется линейным
оператором
(линейным
преобразованием),
действующим из
называется линейным
оператором
(линейным
преобразованием),
действующим из ![]() в
в ![]() ,
если оно удовлетворяет следующим двум
условиям:
,
если оно удовлетворяет следующим двум
условиям:
![]()
![]() ;
;
![]()
![]() ,
,
![]() .
.
Совокупность условий 1 и 2 равносильна следующему условию:
![]() .
(7.1.1)
.
(7.1.1)
Обозначим
через ![]() множество всех линейных операторов,
действующих из линейного пространства
множество всех линейных операторов,
действующих из линейного пространства
![]() в линейное пространство
в линейное пространство ![]() .
Два линейных оператора
.
Два линейных оператора ![]() и
и ![]() из
из ![]() называются равными,
если
называются равными,
если
![]() .
(7.1.2)
.
(7.1.2)
Множество![]() будет линейным пространством над полем
будет линейным пространством над полем
![]() ,
если определить сумму
,
если определить сумму
![]() операторов
операторов
![]() и произведение
и произведение
![]() оператора
оператора
![]() на число
на число
![]() соотношениями
соотношениями
![]()
![]() (7.1.3)
(7.1.3)
![]()
![]() (7.1.4)
(7.1.4)
Нулевым
вектором пространства ![]() будет нулевой
оператор
будет нулевой
оператор
![]() из
из
![]() в
в![]() ,
т.е. оператор, переводящий любой вектор
,
т.е. оператор, переводящий любой вектор
![]() линейного пространства
линейного пространства ![]() в нулевой вектор линейного пространства
в нулевой вектор линейного пространства
![]() .
.
В
случае, когда ![]() ,
линейный оператор
,
линейный оператор
![]() называется линейным преобразованием
пространства
называется линейным преобразованием
пространства ![]() .
.
Пусть
![]() -
оператор из
-
оператор из ![]() ,
и пусть
,
и пусть ![]() и
и
![]() -
фиксированные базисы линейных пространств
-
фиксированные базисы линейных пространств
![]() и
и![]() соответственно.
Разложим векторы
соответственно.
Разложим векторы ![]() по базису
по базису ![]() :
:
![]() ,
,
![]() ,
(7.1.5)
,
(7.1.5)
![]()
![]() .
.
Из
коэффициентов этих разложений составим
![]() -
матрицу
-
матрицу
 .
(7.1.6)
.
(7.1.6)
Матрица
![]() называется матрицей
линейного оператора
называется матрицей
линейного оператора
![]() в паре базисов
в паре базисов ![]() и
и
![]() .
Заметим, что столбцами матрицы
.
Заметим, что столбцами матрицы ![]() служат столбцы координат векторов
служат столбцы координат векторов ![]() в базисе
в базисе ![]() ,
т.е. строки коэффициентов из разложений
(7.1.5).
,
т.е. строки коэффициентов из разложений
(7.1.5).
Если
![]() ,
то при нахождении матрицы линейного
оператора фиксируются векторы одного
базиса
,
то при нахождении матрицы линейного
оператора фиксируются векторы одного
базиса ![]() ,
по которому раскладываются
,
по которому раскладываются ![]() .
Записанные столбцами коэффициенты
разложений образуют квадратную матрицу
.
Записанные столбцами коэффициенты
разложений образуют квадратную матрицу
![]() порядка
порядка ![]() .
.
Равные линейные операторы в одном и том же базисе имеют одинаковые матрицы.
Матрицей суммы линейных операторов в фиксированных базисах является сумма матриц слагаемых операторов в тех же базисах.
При умножении линейного оператора на число его матрица умножается на то же число.
Если
![]() и
и
![]() -
соответственно,
-
соответственно,
![]() -
и
-
и
![]() -
мерное линейные пространства над одним
полем
-
мерное линейные пространства над одним
полем
![]() ,
то линейное пространство
,
то линейное пространство
![]() изоморфно
линейному пространству
изоморфно
линейному пространству
![]() -
матриц с элементами из
-
матриц с элементами из
![]() с
операциями сложения матриц и умножения
их на числа из поля
с
операциями сложения матриц и умножения
их на числа из поля
![]() .
.
Пример
1.
Оператор ![]() называется
тождественным
(единичным)
оператором,
если
называется
тождественным
(единичным)
оператором,
если
![]() .
(7.1.7)
.
(7.1.7)
Покажите
линейность оператора ![]() и постройте его матрицу в базисе
и постройте его матрицу в базисе ![]() .
.
Решение.
В силу того, что ![]()
![]() ,
,
убеждаемся в линейности тождественного оператора. Поскольку
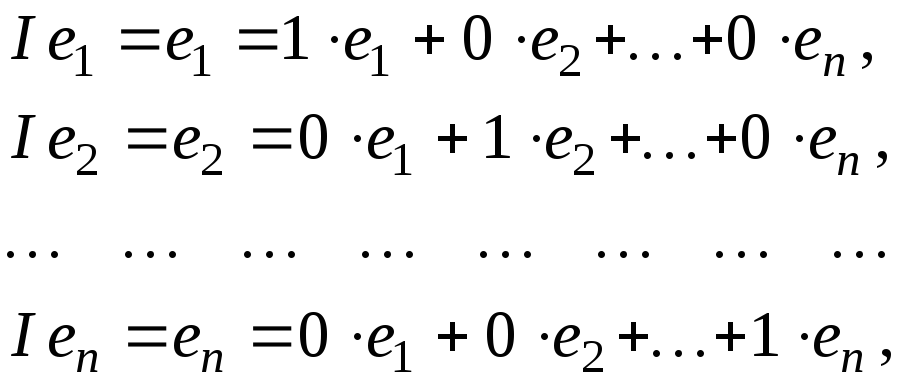
получаем, что
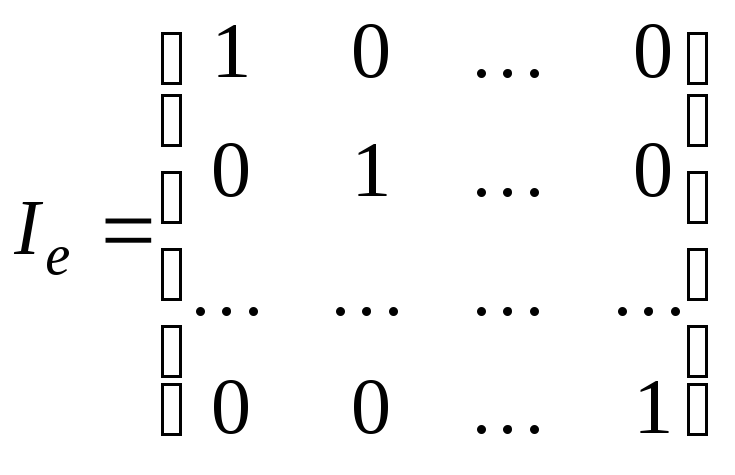 .
.
В любом базисе тождественный оператор имеет единичную матрицу.
Пример 2. Докажите, что преобразование

пространства
![]() линейно и найдите его матрицу в
каноническом базисе.
линейно и найдите его матрицу в
каноническом базисе.
Решение. Пусть
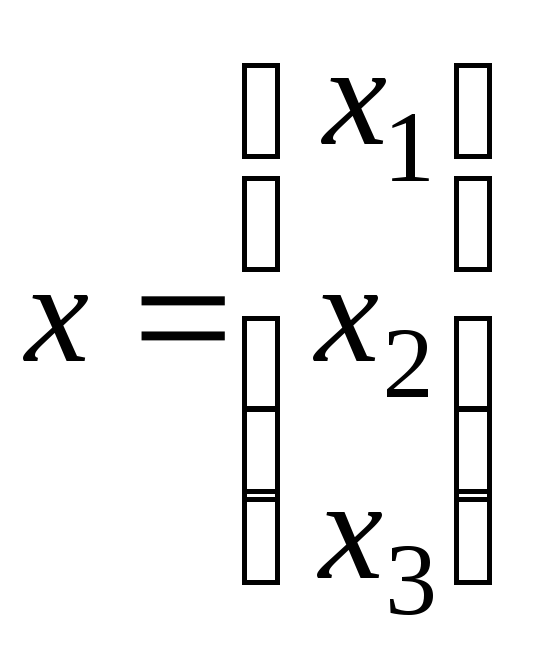 и
и
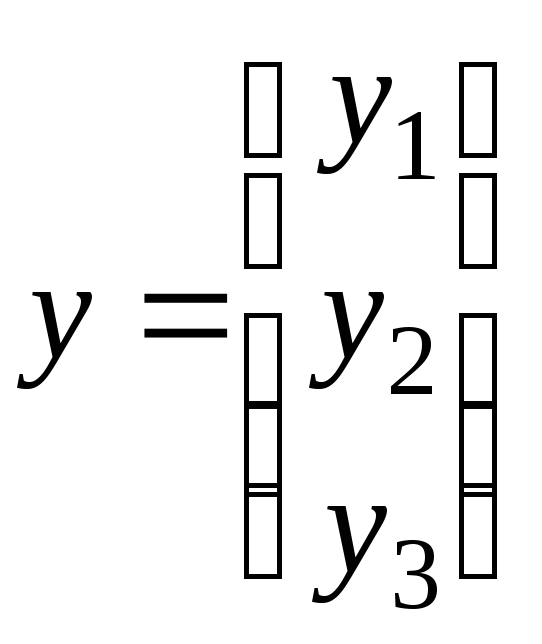 - произвольные векторы из
- произвольные векторы из ![]() .
Тогда
.
Тогда ![]()

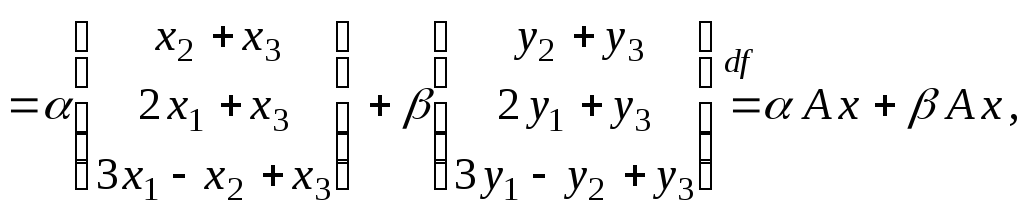
т.
е. преобразование ![]() пространства
пространства ![]() линейно. Канонический базис линейного
пространства
линейно. Канонический базис линейного
пространства ![]() составляют векторы
составляют векторы ![]()
![]() .
Из определения оператора
.
Из определения оператора ![]() вытекает, что
вытекает, что
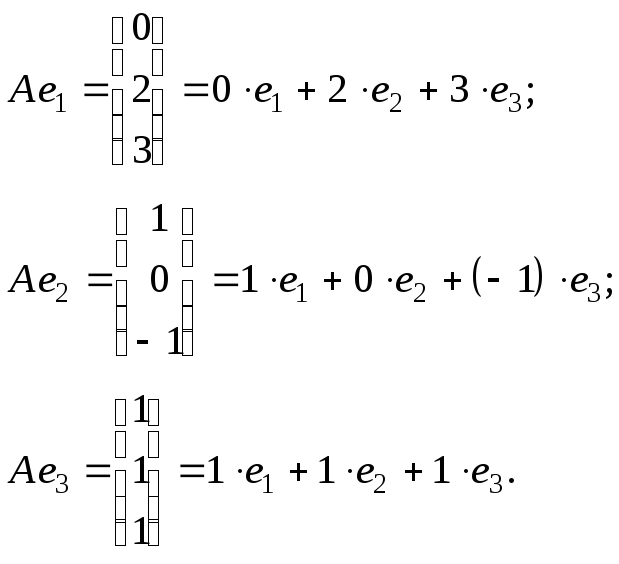
Таким образом,
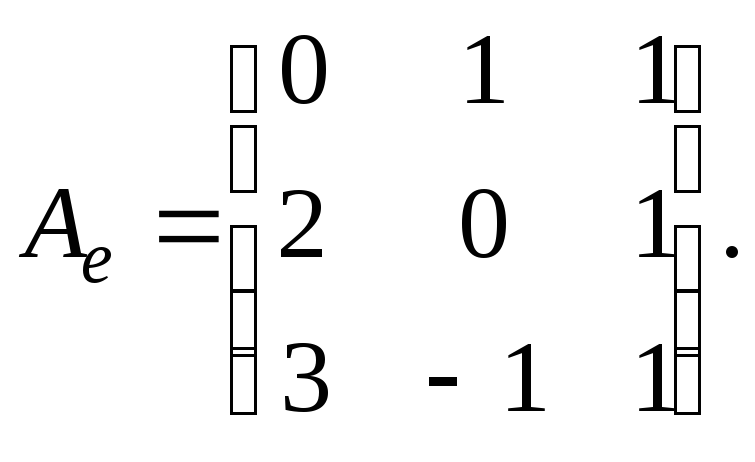
Пример
3.
Покажите, что умножение квадратных
матриц второго порядка слева на данную
матрицу ![]() является линейным преобразованием
пространства
является линейным преобразованием
пространства ![]() и найдите матрицу этого преобразования
в базисе, состоящем из матриц
и найдите матрицу этого преобразования
в базисе, состоящем из матриц
![]()
Решение.
По определению преобразования ![]() для любых матриц
для любых матриц ![]() и любых чисел
и любых чисел ![]() имеем:
имеем:
![]() .
.
Перейдем
к построению матрицы оператора ![]() в данном базисе. В силу того, что
в данном базисе. В силу того, что
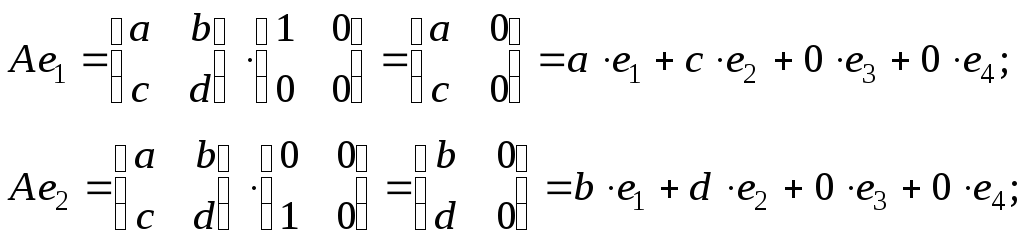

получаем:
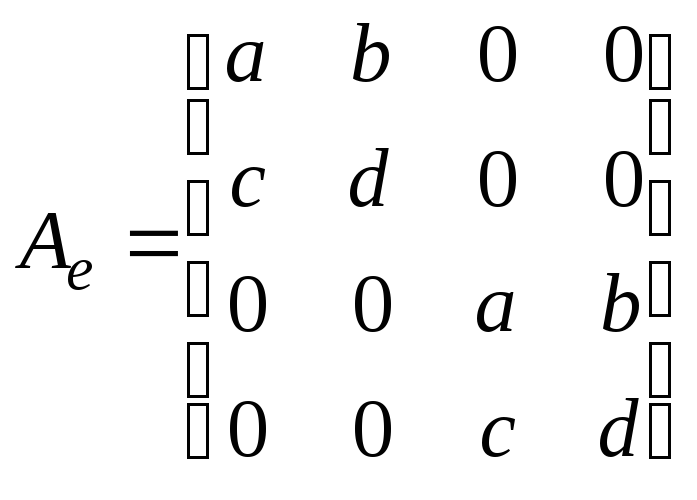 .
.
7.1.1.
Какую матрицу имеет нулевой оператор
в любых базисах пространств ![]() и
и ![]() ?
?
7.1.2.
Линейное пространство ![]() является прямой суммой подпространств
является прямой суммой подпространств
![]() и
и ![]() .
Докажите, что оператор
.
Докажите, что оператор ![]() пространства
пространства ![]() ,
который каждому вектору
,
который каждому вектору ![]() с разложением
с разложением ![]() ,
где
,
где ![]() ,
ставит в соответствие вектор
,
ставит в соответствие вектор ![]() этого разложения, является линейным.
Оператор
этого разложения, является линейным.
Оператор ![]() называется оператором
проектирования
пространства
называется оператором
проектирования
пространства ![]() на
на ![]() параллельно
параллельно ![]() .
.
Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств ![]() и
и ![]() .
.
7.1.3.
Линейное пространство ![]() является прямой суммой подпространств
является прямой суммой подпространств
![]() и
и ![]() .
Докажите, что оператор
.
Докажите, что оператор ![]() ,
который каждому вектору
,
который каждому вектору ![]() с разложением
с разложением ![]() ,
где
,
где ![]() ,
ставит в соответствие вектор
,
ставит в соответствие вектор ![]() ,
является линейным. Оператор
,
является линейным. Оператор ![]() называется отражением
пространства
называется отражением
пространства ![]() в
в ![]() параллельно
параллельно ![]() .
.
Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств ![]() и
и ![]() .
.
7.1.4. Докажите, что всякий линейный оператор, действующий в одномерном пространстве, сводится к умножению всех векторов пространства на фиксированное (для данного оператора) число.
7.1.5. Верно ли, что линейный оператор переводит:
а) линейно зависимую систему векторов в линейно зависимую;
б) линейно независимую систему векторов в линейно независимую?
7.1.6.
Выясните, какие из следующих преобразований
пространства ![]() линейны, и в случае линейности найдите
их матрицы в каноническом базисе:
линейны, и в случае линейности найдите
их матрицы в каноническом базисе:
а)
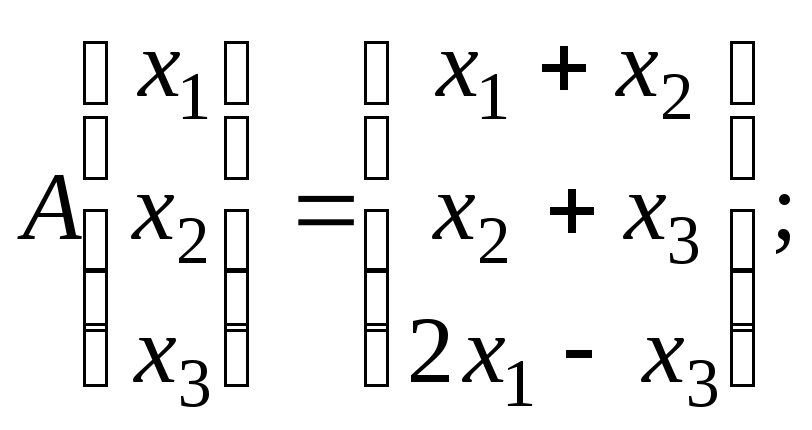 б)
б)
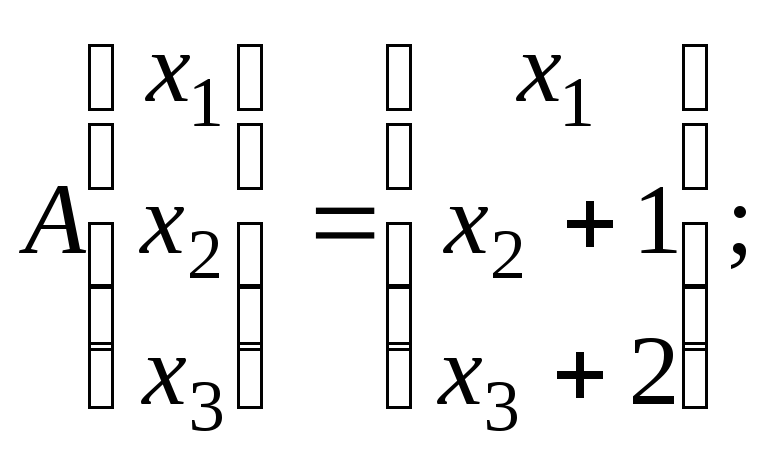
в)
 г)
г)
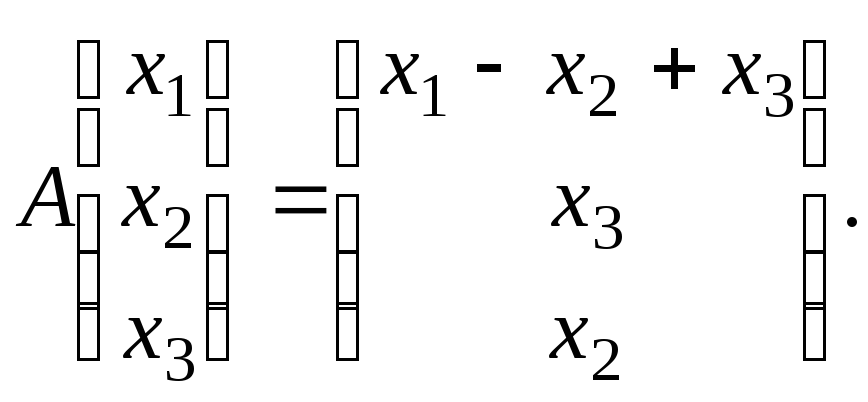
7.1.7.
Укажите, какие из приведенных преобразований
пространства ![]() являются линейными операторами, и
найдите их матрицы в базисе
являются линейными операторами, и
найдите их матрицы в базисе ![]() .
Каждое преобразование описывается
своим действием на произвольный многочлен
.
Каждое преобразование описывается
своим действием на произвольный многочлен
![]() :
:
а)
![]() б)
б) ![]()
в)
![]() ,
где
,
где ![]() и
и ![]() - фиксированные числа, причем
- фиксированные числа, причем ![]() ;
;
г)
![]() Этот оператор в дальнейшем называется
оператором
дифференцирования.
Этот оператор в дальнейшем называется
оператором
дифференцирования.
7.1.8.
Какова матрица оператора дифференцирования,
действующего в линейном пространстве
![]() ,
в базисе
,
в базисе ![]() ,
где
,
где ![]() - действительное число?
- действительное число?
7.1.9.
Покажите, что умножение квадратных
матриц второго порядка справа на данную
матрицу ![]() является линейным преобразованием
пространства
является линейным преобразованием
пространства ![]() ,
и найдите матрицу этого преобразования
в базисе, состоящем из матриц :
,
и найдите матрицу этого преобразования
в базисе, состоящем из матриц :
![]()
7.1.10.
Проверьте линейность оператора ![]() ,
заданного формулой
,
заданного формулой ![]() ,
где
,
где 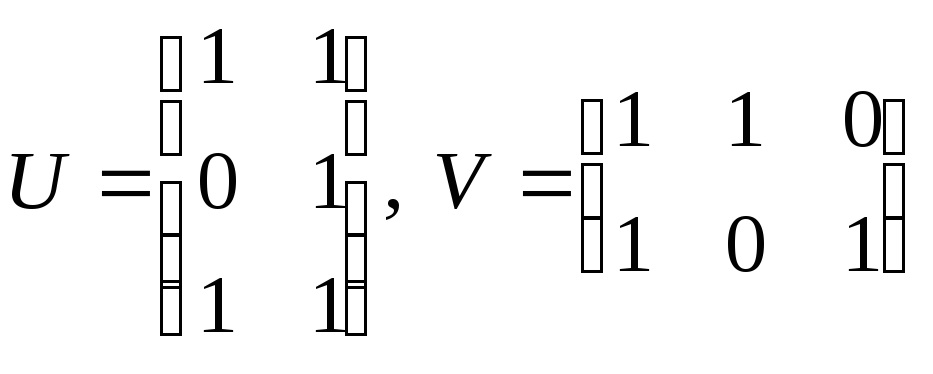 и постройте матрицу этого оператора в
базисах
и постройте матрицу этого оператора в
базисах
![]()
![]() и
и
![]()
7.1.11.
В пространстве ![]() фиксирован базис, состоящий из матриц
фиксирован базис, состоящий из матриц
![]()
(в
указанном порядке). Запишите в этом
базисе матрицу оператора транспонирования,
т.е. оператора, который каждой матрице
![]() ставит в соответствие транспонированную
матрицу.
ставит в соответствие транспонированную
матрицу.
Как
изменится эта матрица, если в базисе
поменять местами векторы ![]() и
и ![]() ?
?
