3Линейка / Задачник-1 / Ответы и указания (1.1)
.DOCОтветы и указания
1.1.2.
46;
;
;
;
.
1.1.3.
Симметрично относительно действительной
оси;
симметрично
относительно начала координат.
1.1.4.
;
.
1.1.5.
.
1.1.6.
если
если
.
1.1.7.
;
;
такого
не
существует.
1.1.8.
;
;
;
,
указание:
воспользуйтесь формулой
;
,
указание:
воспользуйтесь формулами
и
;
2
;
;
.
1.1.10.
Открытая полуплоскость, расположенная
справа от мнимой оси;
полуплоскость,
расположенная ниже горизонтальной
прямой,
проходящей
через точку
рис.
1;
y
z
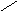-1
1 x
Рис. 1
рис.
2;
y
z
1
x
0
1
Рис. 2
круг
радиуса единица с центром в точке
;
внешняя
часть круга радиуса единица с центром
в точке
;
часть
плоскости, ограниченная эллипсом
;
внешние
точки круга
.
2.1.1.
;
.
2.1.2.
;
;
;
.
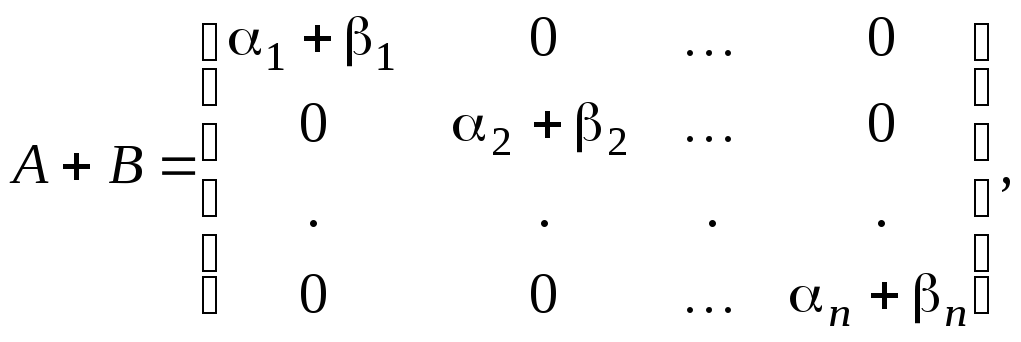
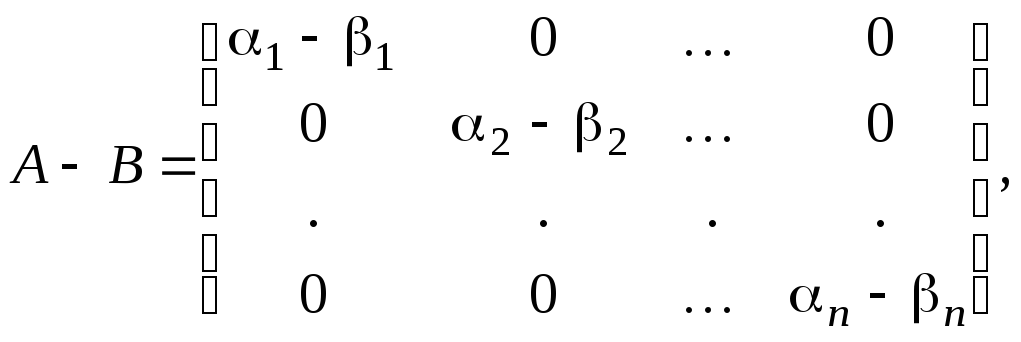
2.1.3.
2.1.4.
;
;
;
.
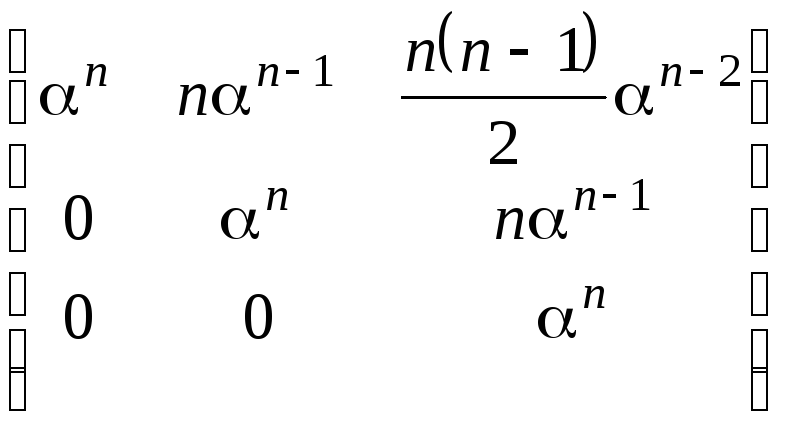2.1.5.
;
;
;
.
2.1.6. Нет.
2.2.1.
Не входит;
входит.
2.2.2.
Со знаком плюс;
со знаком плюс.
2.2.3.
.
2.2.4.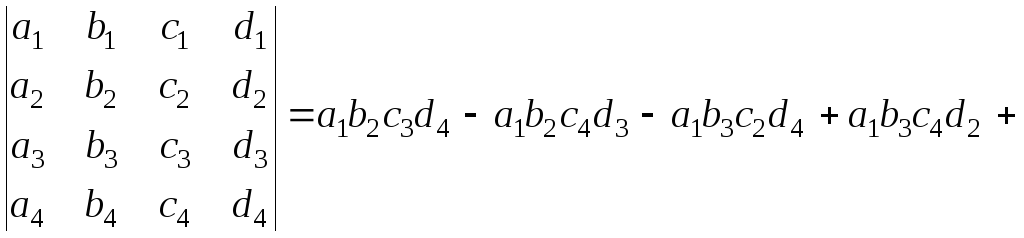
2.2.5.
;
2.2.7.
2.3.1.
.
2.3.3.
2.3.4.
2.3.6.
2.4.1.
систему
нельзя решать по формулам Крамера.
2.4.2.
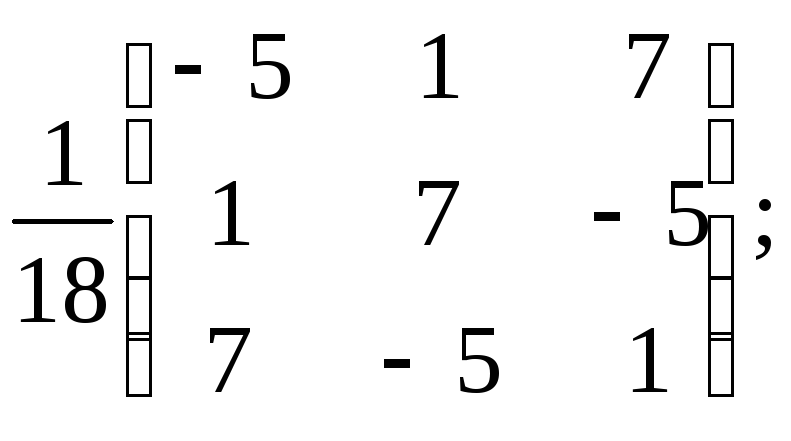
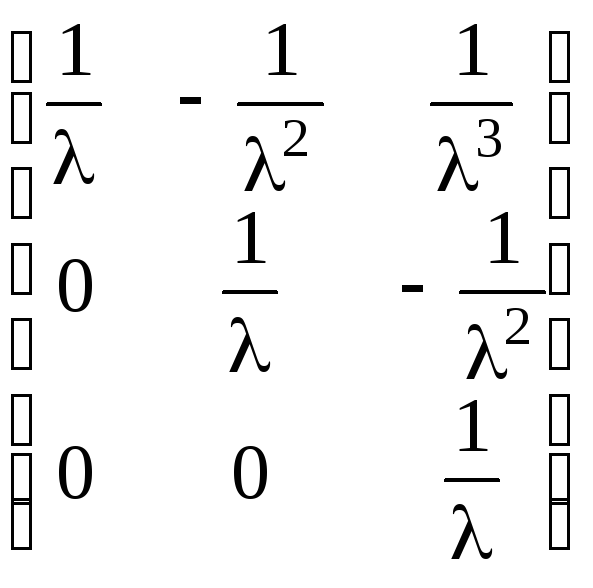если
,
если
2.4.3.
2.4.8.
2.4.9.
3.1.1.
Да, если прямая проходит через точку
;
нет- в противном случае.
3.1.2. Нет.
3.1.3.
Не является;
не является;
является;
является;
не является.
3.1.5.
3.1.6.
Да;
да;
нет;
да.
3.1.7.
Да;
нет;
нет;
да.
3.1.8. Да.
3.2.3. Да.
3.2.4.
3.2.6.
система
линейно зависима.
3.2.7.
в обоих случаях. Система линейно зависима.
3.2.8.
.
3.2.11.
Да;
нет;
нет;
нет;
нет.
3.3.1.
Все векторы вида
;
все
многочлены степени
,
т.е.
;
все
матрицы вида
.
3.3.2. Нет.
3.3.5.
любая
подсистема длины
,
кроме
3.3.6.
и
и
3.3.7. Да.
3.4.1.
его
базисом является любое число, отличное
от 1;
размерность
равна трём,
размерность
равна двум,
размерность
равна двум,
3.4.2.
Например,
и
3.4.3.
3.4.4.
3.4.5.
Можно,
можно,
3.4.6.
Да;
нет.
3.4.7.
3.5.1.
Не является подпространством;
не
является подпространством;
не
является подпространством;
является
подпространством размерности
.
Базис образуют, например, векторы
является
подпространством размерности
.
Базис образуют векторы
является
подпространством размерности
,
базис образуют, например, матрицы
где
-
матрица, у которой элементы
,
а все остальные элементы- нули;
является
подпространством размерности
,
базис образуют, например, матрицы
не
является подпространством.