§ 5.4. Унитарное пространство

Говорят, что в комплексном линейном пространстве определено скалярное произведение, если каждой паре векторов поставлено в соответствие комплексное число, обозначаемое , причем это соответствие удовлетворяет следующим аксиомам:

при и при .

Черта в первой аксиоме означает комплексное сопряжение.

Комплексное линейное пространство, в котором определено скалярное произведение векторов, называется унитарным пространством.

Для любых двух векторов и унитарного пространства справедливо неравенство Коши- Буняковского:

.

В унитарном пространстве, как и в евклидовом, длину вектора определяют формулой

.

Понятие угла между векторами в унитарном пространстве не вводят. Рассматривают лишь случай ортогональности векторов. При этом, как и в евклидовом пространстве, ортогональными считают векторы и , удовлетворяющие условию

Процесс ортогонализации системы векторов, понятие ортогонального и ортонормированного базиса, ортогонального дополнения, ортогональной проекции вектора на подпространство и вообще вся теория евклидова пространства распространяется на унитарное пространство без изменения определений и общих схем рассуждений. Тем не менее каждый раз следует быть внимательным при применении скалярного произведения, поскольку в унитарном пространстве скалярное произведение существенно отличается от скалярного произведения в евклидовом пространстве.

Если - ортонормированный базис - мерного унитарного пространства и для векторов имеют место разложения

то справедливы равенства:

Пример 1. Ортонормируйте систему векторов

считая, что векторы заданы координатами в ортонормированном базисе.

Решение. Сначала проведем процесс ортогонализации данной системы векторов. Положим и найдем из условия

Получим

Поэтому

Теперь положим и будем искать из условий:

Отсюда получаем:

Поэтому

Система векторов ортогональная. Нормируем каждый вектор этой системы:

Пример 2. Докажите, что векторы и унитарного пространства ортогональны тогда и только тогда, когда для любых чисел и .

Доказательство. Необходимость. Пусть . Тогда

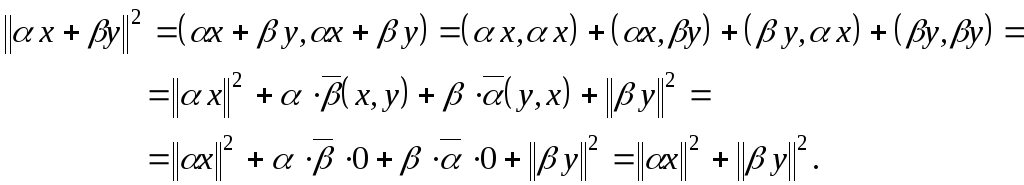
Достаточность. Пусть . Тогда из записанного выше следует, что или

Положим в последнем равенстве . Тогда . Пусть теперь . Тогда . Следовательно, .

5.4.1. Докажите, что из аксиом скалярного произведения в унитарном пространстве вытекают следующие свойства:

для любых векторов унитарного пространства;

для любых векторов унитарного пространства и любого комплексного числа ;

5.4.2. Докажите, что в любом комплексном линейном пространстве можно определить скалярное произведение.

5.4.3. Введите скалярное произведение в - мерном комплексном арифметическом пространстве .

5.4.4. Введите скалярное произведение в пространстве многочленов с комплексными коэффициентами степени .

5.4.5. Докажите, что в произвольном унитарном пространстве остается справедливой теорема Пифагора: если векторы и ортогональны, то . Покажите вместе с тем, что обратное к теореме Пифагора утверждение неверно.

5.4.6. Докажите, что утверждение задачи 5.2.5.

справедливо и в унитарном пространстве.

5.4.7. Докажите равенство:

5.4.8. Пусть . Найдите длины этих векторов и скалярные произведения и считая, что векторы заданы координатами в ортонормированном базисе.

5.4.9. Убедитесь, что система векторов - ортогональная и дополните ее до ортогонального базиса трехмерного унитарного пространства, считая, что векторы заданы координатами в ортонормированном базисе.