Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3Линейка / Задачник-1 / Глава 5.DOC

Скачиваний:

236

Добавлен:

27.03.2015

Размер:

2.16 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Глава 5 Евклидовы и унитарные пространства

§ 5.1. Определение евклидова пространства

Говорят, что в действительном линейном пространстве определено скалярное произведение, если каждой паре векторов поставлено в соответствие действительное число, обозначаемое , причем это соответствие удовлетворяет следующим аксиомам:

при и при .

Действительное линейное пространство, в котором определено скалярное произведение векторов, называется евклидовым пространством.

Для любых двух векторов и евклидова пространства справедливо неравенство Коши- Буняковского:

Знак равенства в имеет место тогда и только тогда, когда векторы и коллинеарны.

Пример. Докажите, что скалярное произведение в арифметическом пространстве можно ввести по формуле: если , то

Доказательство. Покажем, что аксиомы скалярного произведения выполняются:

Пусть . Тогда

, причем равенство нулю возможно, если , т.е. .

5.1.1. Докажите, что из аксиом скалярного произведения вытекают следующие свойства:

для любых векторов евклидова пространства;

для любых векторов евклидова пространства и любого действительного числа ;

5.1.2. Докажите, что в любом действительном линейном пространстве можно определить скалярное произведение.

5.1.3. Введите скалярное произведение в - мерном арифметическом пространстве .

5.1.4. Введите скалярное произведение в пространстве многочленов с действительными коэффициентами степени .

5.1.5. Пусть - квадратные матрицы порядка над полем . Покажите, что формула определяет скалярное произведение в линейном пространстве матриц .

5.1.6. Пусть и - произвольные векторы арифметического пространства . Какая из следующих формул определяет скалярное произведение:

5.1.7. Докажите, что скалярное произведение в можно задать формулой

в том и только том случае, если одновременно и .

5.1.8. Пусть - фиксированный вектор евклидова пространства , - фиксированное действительное число. Будет ли множество всех векторов , для которых , линейным подпространством пространства ?

5.1.9. Линейное пространство разлагается в прямую сумму подпространств . На каждом из подпространств определено скалярное произведение. Докажите, что можно ввести скалярное произведение во всем пространстве , положив: если и - произвольные векторы из с разложениями по подпространствам соответственно и , то

где скалярное произведение вычисляется по правилу, заданному в .

5.1.10. В арифметическом пространстве для векторов и вида

определено скалярное произведение

а для векторов и вида

- скалярное произведение

Введите (по способу, описанному в задаче 5.1.9.) скалярное произведение во всем пространстве . Вычислите по полученному правилу скалярное произведение векторов и .

§ 5.2. Длины и углы. Ортогональность. Процесс ортогонализации Грама- Шмидта. Ортонормированный базис

Вещественное или комплексное линейное пространство называется нормированным пространством, если каждому вектору поставлено в соответствии вещественное число , называемое нормой (или длиной) вектора , причем выполнены следующие аксиомы:

, если

или

Третья аксиома называется неравенством треугольника ( или неравенством Минковского).

Всякое евклидово пространство является нормированным, если в нем норму любого вектора определить равенством

Углом между ненулевыми векторами евклидова пространства называется угол, косинус которого определяется соотношением

Если среди векторов есть хоть бы один нулевой, то угол между такими векторами считается неопределенным.

Два ненулевых вектора и называются ортогональными, если угол между ними равен , т.е. если .

Система векторов называется ортогональной, если в ней все векторы попарно ортогональны.

Во всяком евклидовом пространстве справедлива теорема Пифагора: если векторы и ортогональны, то .

Вектор называется нормированным, если .

Система векторов называется нормированной, если нормированы все ее векторы.

Любой ненулевой вектор можно нормировать, если умножить его на число .

Нормированная ортогональная система векторов называется ортонормированной.

Во всяком - мерном евклидовом пространстве существует ортонормированный базис.

Любую ортонормированную систему векторов можно дополнить до ортонормированного базиса.

От любой линейно независимой системы векторов евклидова пространства можно перейти к ортогональной системе , состоящей из ненулевых векторов. Такой переход совершается с помощью процесса ортогонализации Грама- Шмидта по следующим формулам:

Если процесс ортогонализации применять к линейно зависимой системе векторов, то на некотором шаге обязательно получится нулевой вектор.

Пусть - ортонормированный базис - мерного евклидова пространства и для векторов имеют место разложения

В этом случае справедливы равенства:

Пример 1. Применяя процесс ортогонализации Грама- Шмидта и нормирование векторов, постройте ортонормированный базис подпространства, натянутого на заданную систему векторов

Считайте, что в скалярное произведение векторов и задано формулой

Решение. Прежде всего найдем размерность линейной оболочки , которая будет совпадать с рангом системы векторов :

т.е. .

По формулам получим ортогональную систему векторов :

Нормируя векторы , придем к ортонормированной системе векторов:

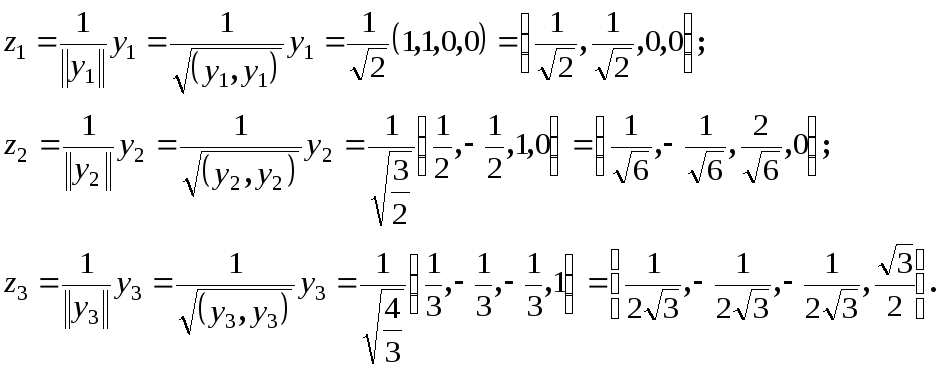
Система векторов является искомым ортонормированным базисом подпространства .

Пример 2. Дополните ортонормированную в смысле скалярного произведения систему векторов до ортонормированного базиса пространства

Решение. Поскольку , систему векторов необходимо дополнить до ортонормированного базиса еще двумя векторами . Решение задачи проведем в два этапа. Сначала систему векторов дополним до ортогонального базиса , а затем векторы и пронормируем.

Пусть . В силу того, что и , записываем в матричном виде однородную систему линейных уравнений, решая которую получаем:

- свободные переменные;

Выбрав , фиксируем

Аналогично найдем . Единственное отличие состоит в том, что теперь решать придется однородную систему не из двух, а из трех уравнений: , и .

- свободная переменная;

Положим . Тогда

Построен ортонормированный базис пространства .

Подчеркнем, что данная задача имела не единственное решение. Выбирая значения свободных переменных другими (кроме ), мы получили бы другие векторы и .

5.2.1. Как изменится угол между ненулевыми векторами и , если

умножить вектор на положительное число;

умножить вектор на отрицательное число;

умножить оба вектора на отрицательные числа?

В последующих задачах по аналогии с трехмерным евклидовым пространством упорядоченная тройка векторов и произвольного евклидова пространства рассматривается как треугольник, о котором говорят, что он “натянут на векторы и ”. Точно так же считается, что параллелограмм, натянутый на векторы и , имеет диагоналями векторы и .

5.2.2. В треугольнике, натянутом на векторы и пространства , найдите длины сторон. Определите углы между сторонами треугольника- векторами и . Какие из этих углов естественно считать внутренними углами треугольника, какие- внешними? Скалярное произведение определено формулой .

5.2.3. Сформулируйте и докажите теорему косинусов для треугольника, натянутого на векторы и произвольного евклидова пространства.

5.2.4. Докажите, что в произвольном треугольнике евклидова пространства:

длина каждой стороны не превосходит суммы длин двух других сторон;

длина каждой стороны не меньше, чем абсолютная величина разности длин двух других сторон.

5.2.5. Докажите, что в параллелограмме, натянутом на векторы и , сумма квадратов длин диагоналей равна сумме квадратов длин сторон.

5.2.6. Докажите, что в евклидовом пространстве :

нулевой вектор- единственный, который обладает тем свойством, что он ортогонален ко всем векторам пространства;

если равенство справедливо для любого вектора , то .

5.2.7. Докажите, что если - ортогональная система векторов, то для любых чисел система векторов также будет ортогональна.

5.2.8. Докажите, что если вектор ортогонален к каждому из векторов , то он ортогонален и к любой линейной комбинации этих векторов.

5.2.9. Докажите, что ортогональная система ненулевых векторов линейно независима.

5.2.10. Применив процесс ортогонализации, найдите ортонормированный базис в пространстве многочленов степени не более двух, взяв за исходный базис многочлен , если скалярное произведение многочленов задано формулой: