Дельта-функция в двуХмерном пространстве

Декартовы координаты: ,

Для независимых координат x и y двухмерная δ-функция является произведением одномерных δ-функций

, (2.39)

где . При интегрировании по всей плоскости выполняется нормировка

.

Используем (2.24)

,

получаем интегральное представление двухмерной дельта-функции

, (2.40)

где

, .

Полярные координаты

Положение точки A определяется расстоянием r от начала координат O и углом φ к оси x

, ,.

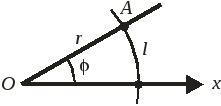
Плоский, или центральный, угол φ является безразмерной частью пространства, ограниченной двумя лучами, и количественно определяется

,

где

l – длина дуги, вырезанной лучами из окружности радиусом r;

радиан от лат. radius – луч.

Угол не зависит от радиуса окружности.

Полный угол равен 2π рад и соответствует длине окружности, тогда

.

Связь с декартовыми координатами. Для точки

, ,

Элемент площади

,

где якобиан преобразования от координат к координатам

;

Дельта-функцию в полярных координатах ищем в виде

,

где . Множитель находим из условия нормировки

.

С учетом нормировки одномерных функций ипринаходим

,

тогда

. (2.41)

Учтено (2.9)

в виде

, .

При имеемцентральную симметрию, поэтому зависимость от угла отсутствует, тогда

.

Ищем из условия нормировки

.

С учетом

получаем

,

. (2.42)

Дельта-функция в трехмерном пространстве Декартовы координаты

,

Для независимых координат x, y и z трехмерная δ-функция является произведением одномерных δ-функций

, (2.44)

где . Интегральное представление находим по аналогии с (2.40)

. (2.45)

Сферические координаты

Положение точки A определяется расстоянием r от начала координат, угловым положением θ по отношению к оси z и угловым положением φ по отношению к оси x

, ,,.

Связь с декартовыми координатами

, ,,

Элемент площади сферы, возникающий при бесконечно малом увеличении углов:

,

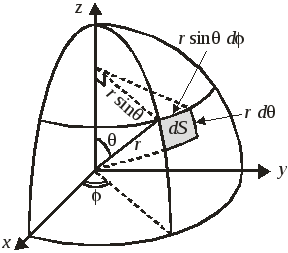
Элемент объема

.

Вычисление на основе якобиана

,

где

,

тогда элемента объема

.

Телесный угол Ω является частью пространства, ограниченной конусом, и количественно определяется

,

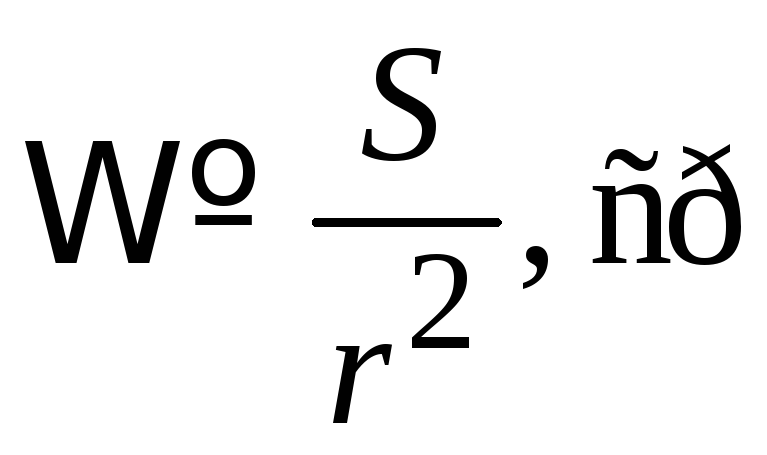где

S – площадь сферического сегмента, вырезанного конусом из сферы радиусом r;

стерадиан – от греч. στερεός – объемный; и лат. radius – луч.

Угол не зависит от выбора радиуса сферы.

Полный угол соответствует , тогда

.

Элемент телесного угла

,

тогда

.

Дельта-функция в сферических координатах. Ищем функцию в виде

,

где . С учетом нормировки

при получаем

,

тогда

, (2.46)

где

,

, , .

При имеемцентральную симметрию, поэтому зависимость от углов отсутствует, тогда

.

Из условия нормировки

,

с учетом

,

,

находим

,

получаем

. (2.50) Гребенчатая функция

Неограниченная периодическая последовательность дельта-функций образует гребенку

. (2.53)

Гребенчатая функция моделирует неограниченную кристаллическую решетку с атомами в узлах, или любые периодические структуры из элементов малого размера.

В (2.53) замена дает

.

Используя теорему (2.8) о масштабном преобразовании аргумента дельта-функции

,

получаем гребенчатую функцию с периодом a

. (2.54)