Пространственное квантование момента импульса
Дискретность квантовых чисел m и l приводят к дискретности значений и направлений момента импульса, описывающего вращающуюся частицу.
Например, при l = 3 получаем
,
,
.
Вектор момента импульса показан на рисунке.
Следовательно:
1. Угол θ ориентации вектора момента импульса L квантуется
,
;
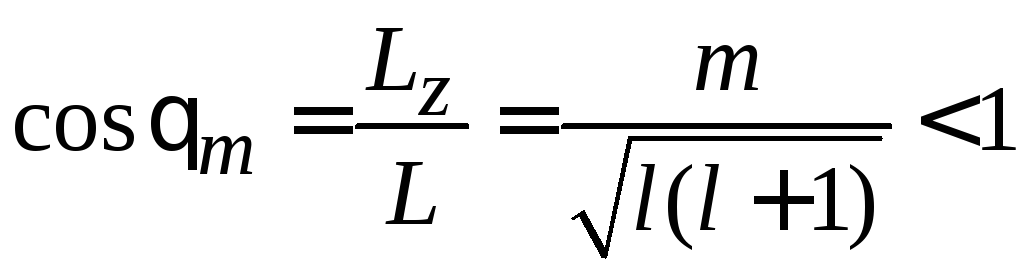2. Угол φ ориентации вектора момента импульса L полностью неопределенный.
3. Вектор момента импульса L не может быть направлен по оси z;
4.
Число возможных проекций вектора
L
равно
.
Решение уравнения (7.16)
С
учетом
уравнение (7.16) получает вид
.
Уравнение
совпадает с уравнением (6.116) для
присоединенной функции Лежандра
,
следовательно
.
(7.21)
С учетом
,
,
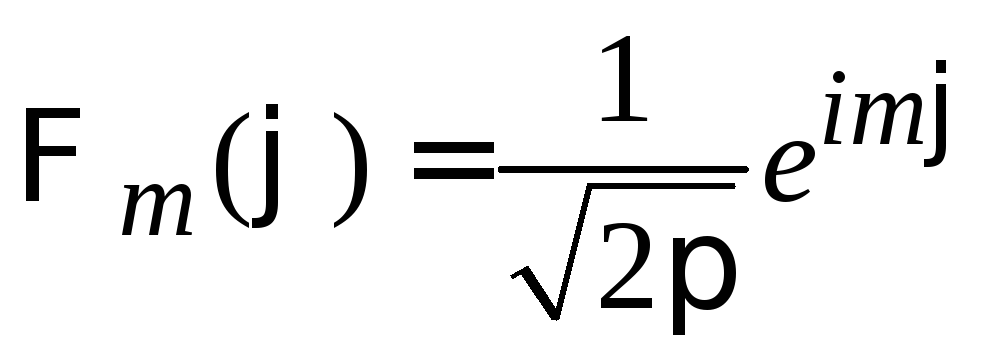получаем сферическую функцию
.
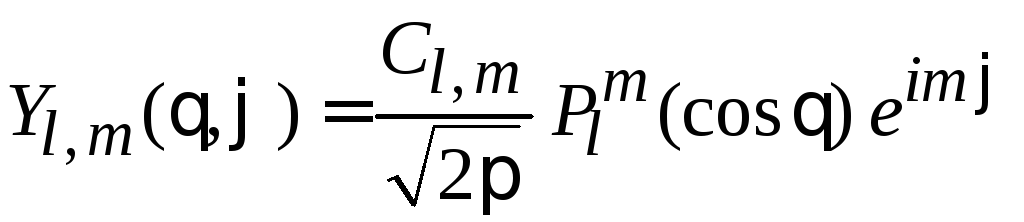(7.22)
Квадрат
модуля сферической функции является
плотностью вероятности обнаружения
состояния в единичном телесном угле
около направления
.
Нормировка вероятности дает
,
.
Подставляем (7.22), учитываем (1.43) и (6.123)
,
,
,
находим коэффициент
.
(7.23)
Результат
получен с точностью до умножения на
постоянный фазовый множитель
,
где α – любое число.
Сферическая функция
В результате
.
(7.24)
При
состояние симметрично относительно
осиz,
зависимость от угла θ описывается
полиномом Лежандра
.
(7.24а)
Из (6.120)
следует соотношение между состояниями с противоположными проекциями момента импульса
.
(7.25)
Обращение движения приводит к комплексному сопряжению функции состояния.
Используем (1.43) и (6.123)
,
,
получаем условие ортонормированности сферических функций
.
(7.27)
Инверсия координат
При
инверсии
меняются углы и сферическая функция
,
.
При этом
,
,
,
,
.
Для
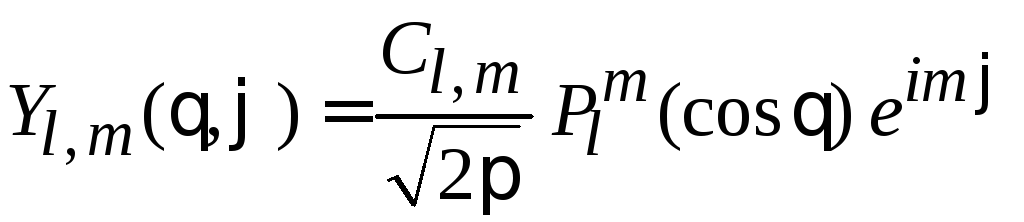
находим
.
(7.28)
При инверсии координат четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.
Функции низших порядков
Используем (7.24)
.
При
;
находим
,
,
,
,
,
,
.
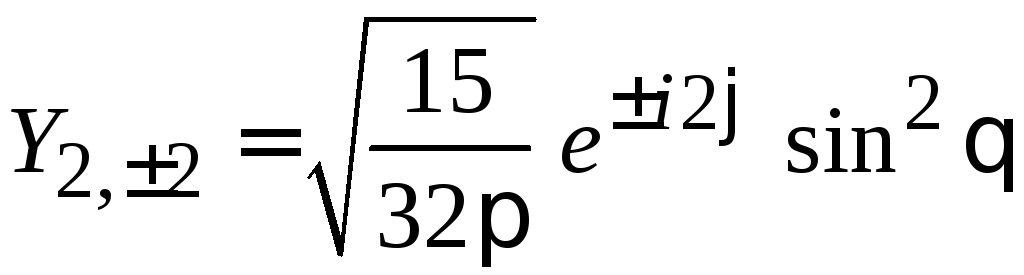(7.29)
При
нет зависимости от углов –центрально-симметричное
состояние;
При
нет зависимости от угла φ –осесимметричное
состояние.
Плотность вероятности
Вероятность обнаружения состояния в единичном телесном угле равна квадрату модуля сферической функции
.
Вероятность не зависит от угла φ, т. е. состояние симметрично при поворотах вокруг оси Оz. Частные случаи распределений показаны на рисунке.
Действие повышающего и понижающего операторов
Найдем действие повышающего и понижающего операторов на сферическую функцию (7.22)
.
Повышающий оператор (7.9), записанный в сферических координатах, имеет вид
.
Действуем на сферическую функцию
.
С учетом
,
,
,
находим
.
Используем рекуррентное соотношение (6.141)
,
тогда
.
Из (7.23)
получаем
.
В результате
.
(7.30)
Выполняется
.
(7.31)
Для доказательства используем (7.12) и (7.20)
,
,
,
получаем
.
На
(7.30) действуем оператором 
.
Левые стороны последних равенств одинаковые, сравнение правых сторон дает
.
Заменяем
,
и получаем (7.31).