Повышающий и понижающий операторы

,

. (7.9)

Действуя на сферическую функцию , операторы изменяют на единицу число m, т. е. проекцию вектора момента импульса на ось z.

Выполняются соотношения

,

, (7.11)

. (7.12)

Доказательство (7.12)

В подставляем (7.9), сохраняя порядок следования сомножителей:

.

Используем (7.2) и (7.8)

,

,

находим

и получаем (7.12).

Уравнение для СферическОй функциИ

Функция определяется как собственная функция оператора квадрата момента импульса

, (7.13)

где –собственное значение оператора ;– постоянная Планка;– неизвестная безразмерная постоянная. Выполнение (7.13) означает, что если объект находится в состоянии, то квадрат момента импульса имеет определенную величину, равную .

С учетом (7.5)

,

из (7.13) получаем уравнение для сферической функции

. (7.14)

Ищем функцию и значения λ.

Разделение переменных

В (7.14) входят вторые производные от аргументов θ и φ в виде слагаемых. Произведения производных с разными аргументами отсутствуют, поэтому аргументы разделены и решение ищем в виде

.

Это решение подставляем в уравнение (7.14), умноженное слева на :

.

Упрощаем уравнение, вынося из под знаков дифференцирования функции, аргументы которых не подвергаются дифференцированию, и группируем слагаемые с одинаковыми аргументам

.

Левая и правая стороны имеют разные аргументы, поэтому обе стороны равны постоянной . В результате получаем независимые уравнения

, (7.15)

. (7.16)

Неизвестными являются , ,λ и .

Решение уравнения (7.15)

1. Уравнение (7.15) является уравнением Гельмгольца и имеет решение

,

что проверяется прямой подстановкой.

2. При увеличении угла φ на 2π система возвращается в исходное положение, поэтому на функцию состояния накладываем условие периодичности

,

в явном виде

,

следовательно

.

Получаем условие квантования

,

–магнитное число,

в результате

.

3. Квадрат модуля функции состояния является плотностью вероятности обнаружения состояния. Накладываем условие нормировки вероятности

,

находим

,

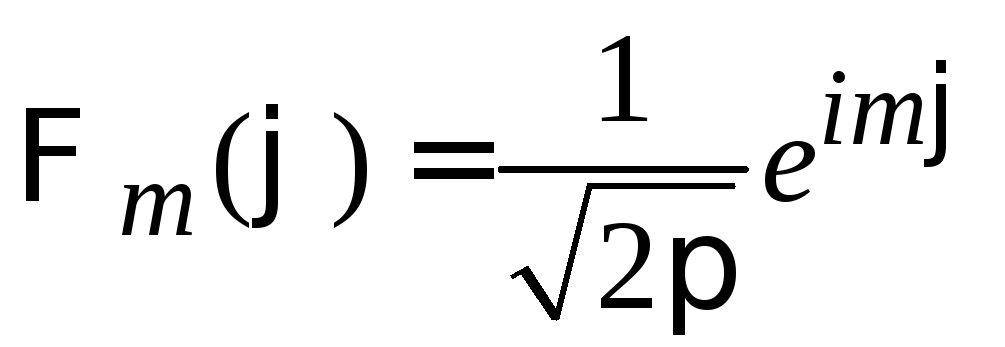. (7.17)

Результат получен с точностью до умножения на постоянный фазовый множитель , где α – любое число.

На основании формулы (1.43)

,

из раздела «Преобразование Фурье», базис функций , где , удовлетворяет условию ортонормированности

. (7.18)

4. Оператор проекции момента импульса (7.4)

.

Функция (7.17)

и сферическая функция

удовлетворяют

,

. (7.19)

Следовательно, и являются собственными функциями оператора проекции момента импульса на ось z с собственным значением . В состоянии, описываемом функцией, измерение проекции момента импульса на осьz дает результат

.

Значение 

Найдем величину постоянной λ в уравнении

.

1. Оператором (7.11)

действуем на функцию и используем (7.19)

,

получаем

.

Следовательно, операторы переводят состояние с собственным значениемm в состояния с собственными значениями , т. е.–повышающий оператор, –понижающий оператор.

2. Проекция вектора не превышает его модуль. Если максимальная проекция

,

то нет состояний с , тогда действие повышающего оператора на состояние с максимальной проекцией дает нуль

.

3. Действуем на оператором

. (7.12)

Используем

(7.19)

и

, (7.13)

получаем

.

Находим

.

4. В результате получены уравнения для сферической функции

,

, (7.20)

где

–магнитное число;

–орбитальное число;

–проекция момента импульса на ось z;

–модуль момента импульса.