Гамма- и бета-функции эйлера
Гамма-функция Г(x) и бета-функция В(x) используются во множестве математических и физических задач и формул. Гамма-функция является обобщением факториала
,
,
на случай дробного и/или отрицательного n.
Гамма-функция
.
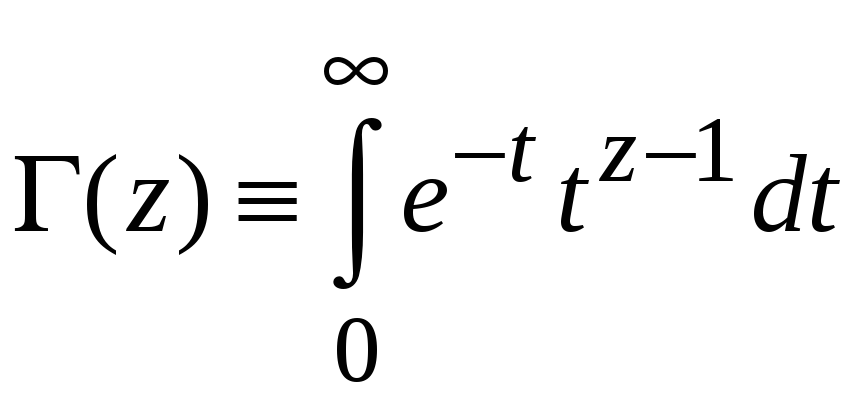(4.1)
Функцию
исследовал Леонард Эйлер в 1730 г. Сходимость
интеграла на верхнем пределе обеспечивает
функция
.
Сходимость на нижнем пределе зависит
от величины z.
При целом отрицательном и нулевом z
интеграл расходится.
Анализ интеграла
Область
интегрирования
разбиваем на участки
и
,
где
,
.
-
Функция
конечна при любых z.
Доказательство
На
верхнем пределе
убывает с ростом t
быстрее любой степенной функции, и
интеграл сходится при любых z.
На нижнем пределе интеграл конечен при любых z
-
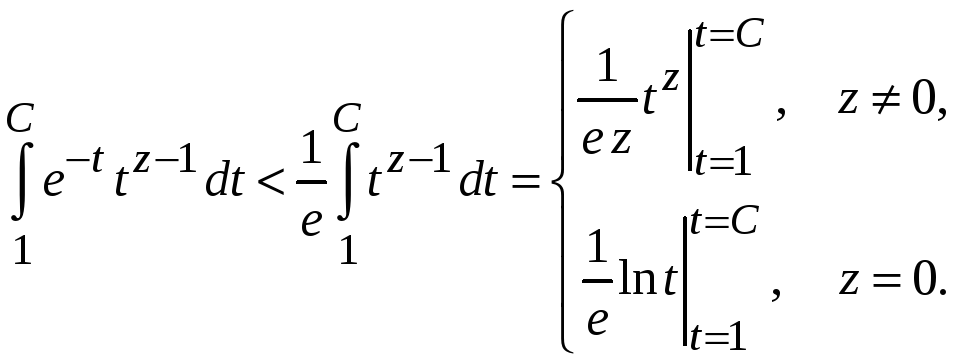
Функция
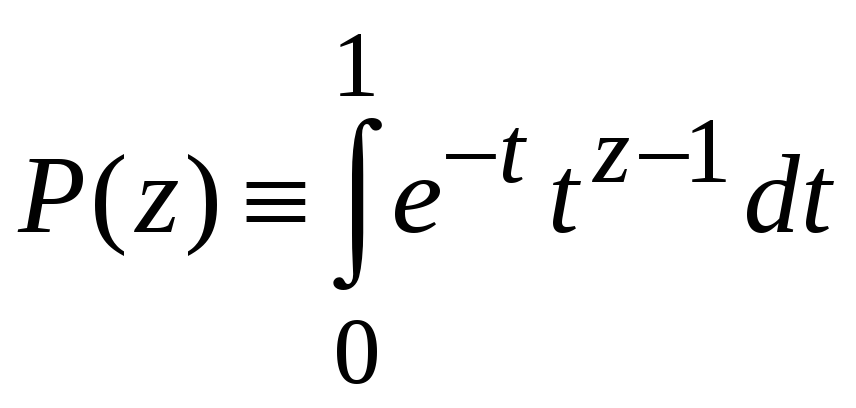имеет полюса первого порядка при
Доказательство
Учитывая
,
разлагаем в ряд Маклорена
,
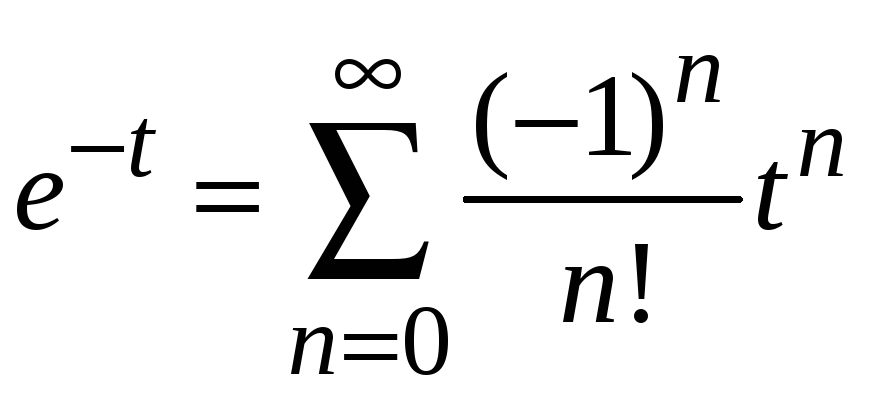получаем
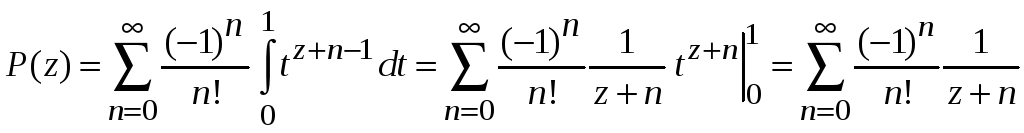
При
положительном
используем
,
тогда
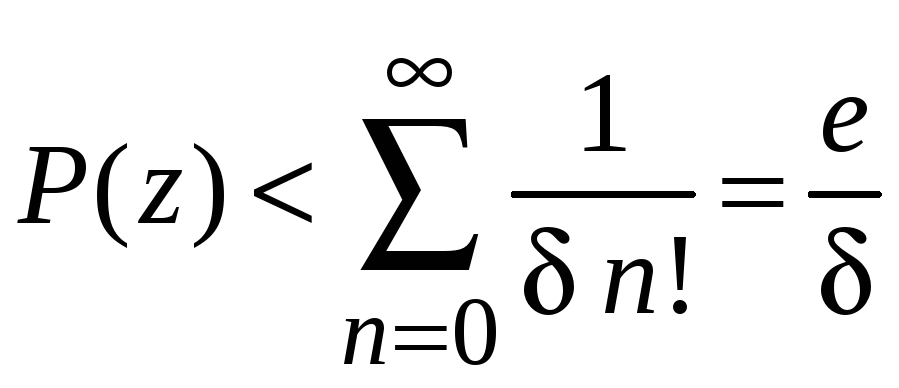– конечное,
где учтено
.
При отрицательном , где ; , для
Получаем
.
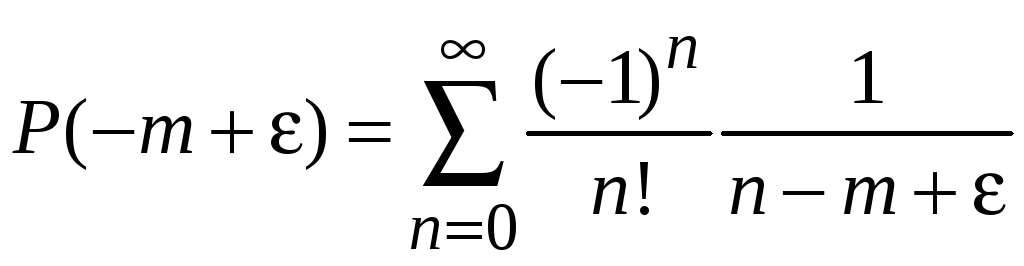Одно
слагаемое
дает полюс первого порядка, остальные
слагаемые конечные и ими пренебрегаем
вблизи полюсов, тогда
,
(4.3)
,
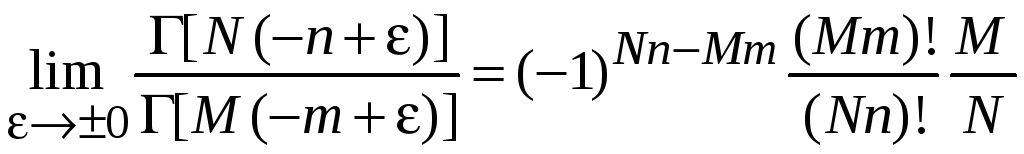(4.4)
где
Доказательство (4.4)
Используя (4.3), получаем:
.
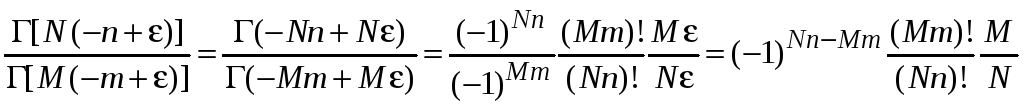В
точках
функция
имеет полюса первого порядка.
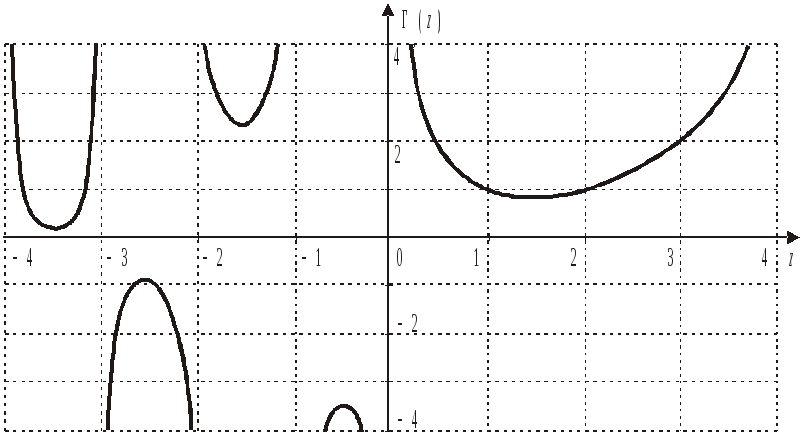
График гамма-функции
Далее будут доказаны значения для ряда точек на рисунке:
,
,
,
,
.
Экстремальные значения
на
положительной полуоси
;
на
отрицательной полуоси
,
,
,
...
Рекуррентное соотношение
В рекуррентном соотношении, от лат. recurro – «возвращаться», рассматриваемая функция встречается два и более раз.
Интегрируем (4.1)
по частям, полагая:
,
,
,
.
Слагаемое
uv
равно нулю на обоих пределах при
,
слагаемое
сводится к гамма-функции. В результате
.
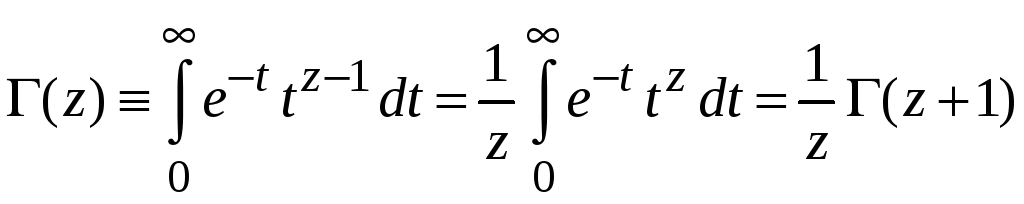При
получаем рекуррентное соотношение
.
(4.5)
Связь с факториалом
Используем
(4.1) при
,
тогда из (4.5) находим:
при
,
;
при
,
;
при
,
;
по индукции
.
В результате
,
(4.6)
.
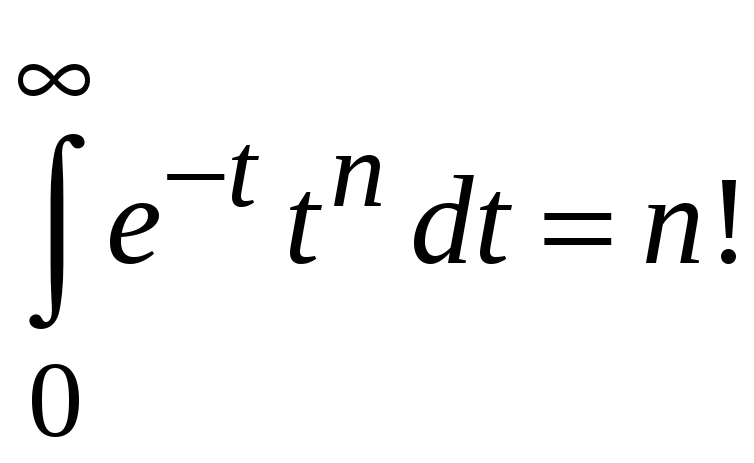(4.7)
Интегралы, выражающиеся через гамма-функцию
Из (4.1) получим новые формулы для интегралов, усложняя аргумент интегрирования.
1. В интеграле
замена
,
,
,
,
дает
.
Переобозначаем
и находим
.
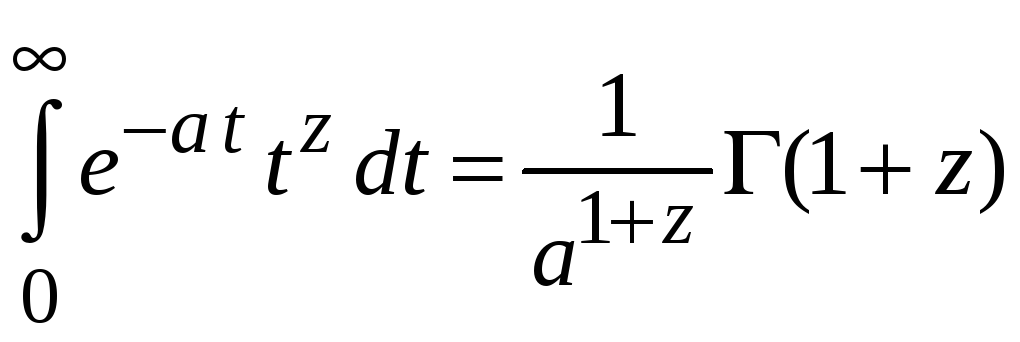(4.8)
-
В (4.8) полагаем
,
,
,
получаем
.
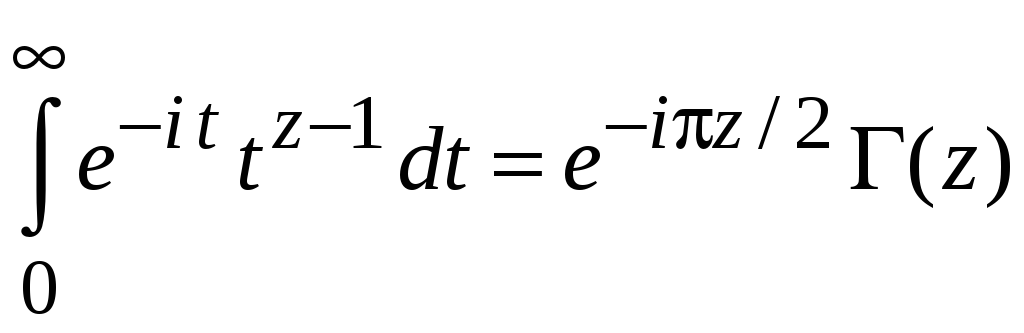Разделяем выражение на вещественную и мнимую части, используя формулу Эйлера:
,
находим
,
.
(4.8а)
3. В интеграле (4.8)
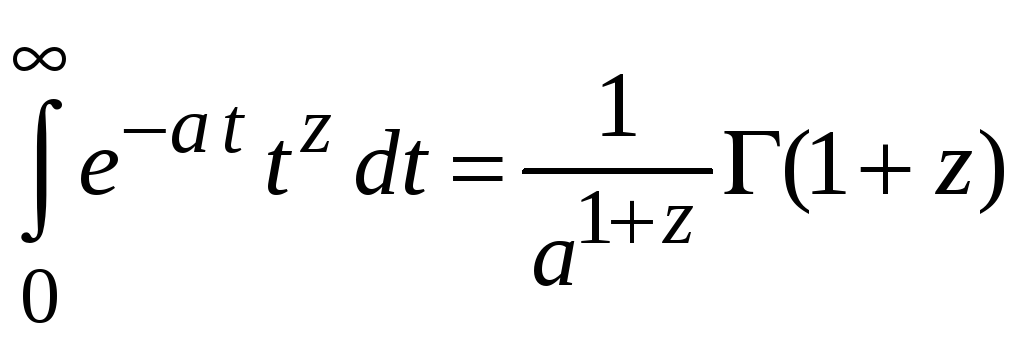
заменяем аргумент
,
,
,
получаем
.
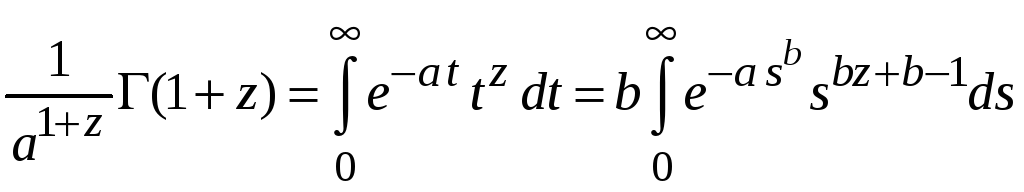Заменяем
параметр
,
тогда
,
,
В полученном выражении
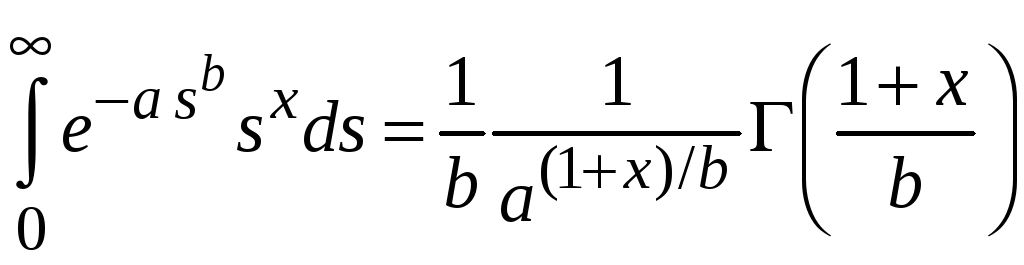
переобозначение
и
дает
.
(4.9)